Метод усреднения.
Пусть прогноз различными методами дает множество значений в порядке возрастания 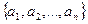 . Предположим, что величина спроса
. Предположим, что величина спроса 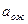 есть случайная величина, распределенная по
есть случайная величина, распределенная по 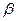 - распределению. Математическое ожидание определим по формуле
- распределению. Математическое ожидание определим по формуле
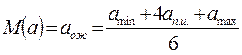
а дисперсия
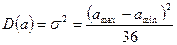 ,
,
где:
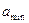 - минимальная величина прогнозируемого спроса
- минимальная величина прогнозируемого спроса
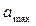 - максимальная величина прогнозируемого спроса
- максимальная величина прогнозируемого спроса
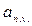 - наиболее вероятная величина спроса
- наиболее вероятная величина спроса
В нашем случае 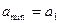 ,
, 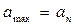 ,
, 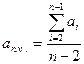 .
.
Если предположить, что величина спроса есть случайная величина, распределенная по нормальному закону, то можем записать:
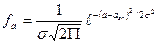
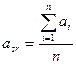
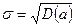
Тогда вероятность того, что величина спроса а будет меньше ожидаемой величины 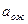 :
:
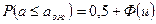 ,
,
где 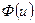 - функция Лапласа.
- функция Лапласа.
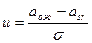 .
.
Значения функции 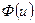 табулированы. Поэтому, задавая требуемый уровень вероятности появления прогнозированной величины спроса, можно определить значение
табулированы. Поэтому, задавая требуемый уровень вероятности появления прогнозированной величины спроса, можно определить значение 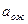 .
.
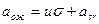 .
.
Дата добавления: 2015-01-13; просмотров: 727;
