ПРИМЕР 6

Ниже показаны данные спроса на электрические генераторы компании за период 1986—1992 гг. Подберем прямую линию тренда к этим данным и определим прогноз спроса в 1993 г.

Имея серию данных за период, мы должны минимизировать расчеты, транс­формируя значения х (время) в простые числа. Так, в данном случае мы должны обозначить 1986 год как год 1, 1987-й — как год 2 и т. д.

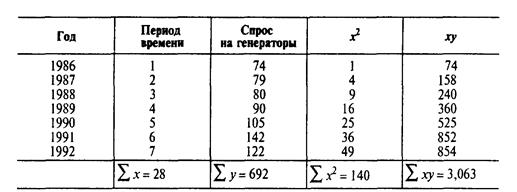
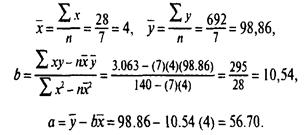
Следовательно, уравнение, полученное методом наименьших квадратов, имеет вид у = 56,70 + 10,54х. Проектируя спрос в 1993 году, мы, в первую очередь,

определяем 1993 год в нашей новой кодовой системе как х = 8:

(Продажи в 1993 г.) =56,70 + 10,54 (8) = 141,02, или 141 генератор. Мы должны оценить спрос для 1994 года, подставив х = 9 в уравнение:

(Продажи в 1994 г.) = 56,70 + 10,54 (9) = 151,56, или 152 генератора. Проверив валидность модели, мы наносим на диаграмму (рис. 4.5) бывший спрос и линию тренда. В этом случае мы можем быть осторожными и попытаться понять колебания в спросе в 1991—1992 гг.

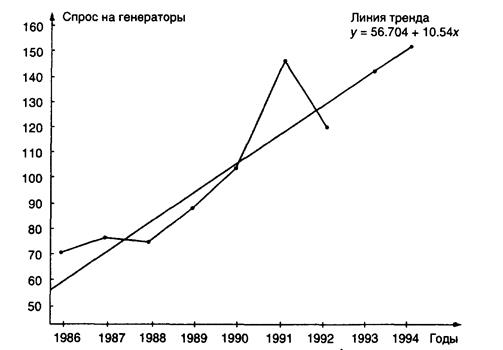
Рис. 4.5. Электрические генераторы и расчетная пиния тренда

5. СЕЗОННЫЕ КОЛЕБАНИЯ ДАННЫХ

Прогнозирование временных серий, такое, как в примере 6, включает рассмотрение тренда данных в течение серий временных наблюдений. Иногда тем не менее повторяющиеся колебания в определенные сезоны года делают сезонное регулирование про­гноза линии тренда необходимым. Спрос на уголь и топливо, например, обычно возрастает в течение холодных зимних месяцев. Спрос для клубов гольфа может быть наиболее высок летом. Анализ данных в месячном или квартальном разрезе делается легко с использованием статистических моделей, учитывающих сезонность. Сезонные индексы могут затем использоваться в ряде общих методов прогнозирования. Пример 7 иллюстрирует один способ расчета сезонных факторов по прошлым данным.