ПРИМЕР 3

В январе дилер предсказывал февральский спрос для конкретной модели автомобиля Ford равным 142. Текущий февральский спрос был 153 автомобиля. Используя скользящую постоянную α = 20, мы можем прогнозировать спрос марта с помощью модели экспоненциального сглаживания. Подставляя а в формулу, мы имеем:

Новый прогноз (для спроса марта) = 142 + .2 (153 - 142) = 144.2.

Таким образом, спрос в марте этой модели Ford после округления равен 144.

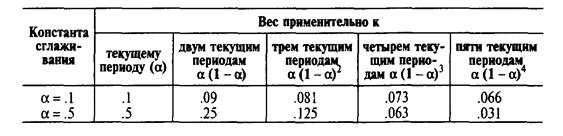
Константа сглаживания а может быть изменена для придания большего веса текущим данным (когда а высока) или большего веса прошлым данным (когда а низка). Для демонстрации этого подхода к весам уравнение (4.4) может быть переписано алгебра­ически в следующей форме:

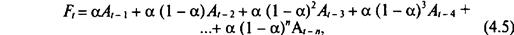
где сумма весов стремится к 1.

Каждая из этих временных серий проходит п периодов (где п может быть очень велико); важно, что прошлые периоды умень­шаются быстрее, когда α возрастает. Когда α стремится к 1,0 и достигает 1,0, тогда уравнение (4.5) имеет вид F_t = 1,0 A_{t - 1}. Все другие значения исчезают, и прогноз становится идентичным простейшей модели, описанной ранее в данной главе. В этом случае прогноз спроса для следующего периода является точно таким, как спрос в текущем периоде.

Предыдущая таблица поможет проиллюстрировать это поло­жение. Например, когда α = 5, мы можем увидеть, что новый прогноз базируется, главным образом, на спросе в прошлые три или четыре периода. Когда α = 1, прогноз имеет малые веса в текущем и ряде предыдущих периодов (около 19) значений спроса.

Выбор константы сглаживания. Метод экспоненциального сглаживания прост в использовании и может быть успешно при­менен в банках, производственных компаниях, оптовой торговле и других организациях. Определение значения константы сглаживания а может дать различия между точным прогнозом и неточ­ным прогнозом. Выбирая значение константы сглаживания, доби­ваются более точных прогнозов. В общем, точность модели про­гнозирования может быть определена сравнением прогнозного значения с текущим, или наблюдаемым, значением. Ошибка про­гноза определяется формулой

Ошибка прогноза = Спрос - Прогноз.

Измерение всех ошибок прогноза для модели является средним абсолютным отклонением (МАD). Оно рассчитывается суммирова­нием абсолютных значение индивидуальных ошибок прогноза и делением на число периодов данных п:

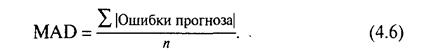
Рассмотрим приложение с тестированием ошибок для двух значений α в примере 4.

ПРИМЕР 4

Порт в Балтиморе имел большие очереди на разгрузку зерна из судов в течение последних восьми кварталов. Торговый операционный менеджер хочет применить экспоненциальное сглаживание, чтобы посмотреть, как хорошо эта техника рабо­тает применительно к тоннажу разгружаемого зерна. Он принимает, что прогноз разгружаемого зерна в первом квартале был 175 тонн. Рассматриваются два значения: α =.10 и α =.50. В следующей таблице показаны детальные расчеты только для α = .10.

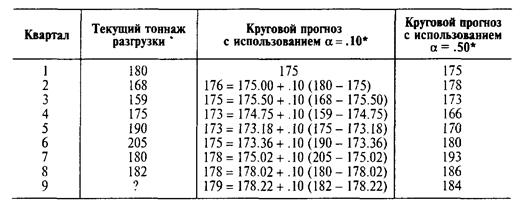
* Прогнозы округляются до целых тонн.

Изменение точности для каждой константы сглаживания мы можем рассчи­тать по абсолютному отклонению и среднему абсолютному отклонению (МАD).

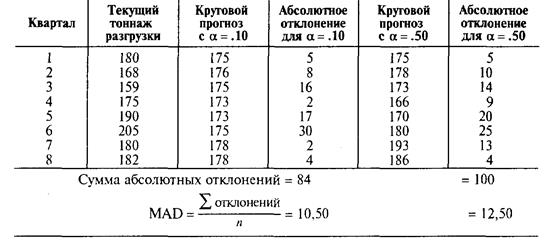
В результате этого анализа константа сглаживания α = .10 яв­ляется предпочтительной по отношению к α = .50, так как ее МАD меньше.

Наряду со средним абсолютным отклонением (МАD), два других измерителя ошибок в прогнозировании иногда использу­ются. Среднеквадратическое отклонение (МSЕ) — это среднее от квадрата разности между прогнозными и наблюдаемыми значе­ниями. Среднее процентное отклонение (МАРЕ) является абсолют­ной разницей между прогнозируемыми и наблюдаемыми значе­ниями в процентах к наблюдаемым значениям.

Экспоненциальное сглаживание с трендовым регулированием. Как и другие методы меняющегося среднего, простое экс­поненциальное сглаживание не приспособлено к регулированию тренда. Иллюстрируя более сложную модель экспоненциального сглаживания, рассмотрим, что требуется для регулирования трен­да. Идея заключается в расчете прогноза простым экспоненциальным сглаживанием, а затем в определении положительного или отрицательного лага в тренде.

Формула имеет вид следующего равенства:

Прогноз, включающий тренд (FIT_t) =

= Новый прогноз (F_t) + Коррекция тренда (Т_t).

Сглаживая тренд, уравнение для коррекции тренда использует константу сглаживания β, так же как в простой экспоненциальной модели использовалась α.

Т_t рассчитывается с помощью равенства

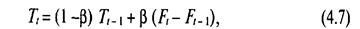
где Т_t — сглаженный тренд для периода Г,

T_{t - 1} — сглаженный тренд для предыдущего периода;

β — константа сглаживания, которую мы выбираем;

F_t — прогноз простого экспоненциального сглаживания для периода;

F_{t - 1} — прогноз для предыдущего периода.

Имеются три шага расчета прогноза с регулируемым трендом.

Шаг 1. Расчет простого экспоненциального прогноза для пе­риода t (F_t).

Шаг 2. Расчет тренда с использованием уравнения

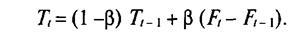
Для начала шага 2 для первого периода начальное значение тренда должно быть заложено (или как хорошее предположение, или как обзор прошлых данных). После этого рассчитывается тренд.

Шаг 3. Расчет прогноза с регулируемым трендом методом экспоненциального сглаживания по формуле FIT_t = F_t + T_t.

ПРИМЕР 5

Большое предприятие использует экспоненциальные сглаживания для прогноза спроса на оборудование для контроля за загрязнением. Считается, что тренд существует.

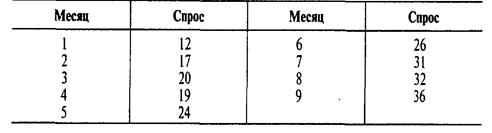
Константы сглаживания определены значениями α = .2 и β = .4. Предполагае­мый начальный прогноз для месяца 1 был 11 единиц.

Шаг 1. Прогноз для месяца 2 (F₂) = Прогноз для месяца 1 (F₁)+(Спрос месяца 1 - Прогноз для месяца 1):

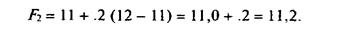
Так, простои экспоненциальный прогноз (без учета тренла) для месяца 2 был равен 11,2 единицам, а прогноз с регулируемым трендом был равен 11,28 едини­цам. В месяце 3 простой прогноз (без учета тренда) был равен 12,36 единицам, а прогноз с регулируемым трендом был равен 12,87 единицам. Естественно, различ­ные значения T₁ и β могут давать даже лучшие оценки.

Следующая таблица содержит прогнозы для девятимесячного периода. Рис. 4.3 сравнивает текущий спрос, прогноз без учета тренда (F_t) и прогноз с учетом тренда (FIT_t).

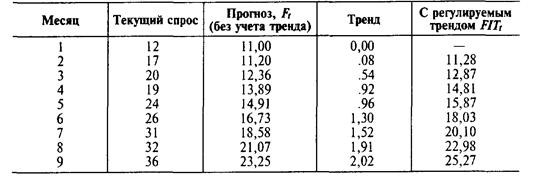
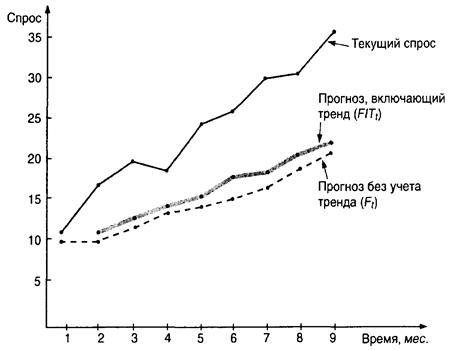
Рис. 4.3. Текущие значения сравнительно с прогнозами

Значение трендовой константы сглаживаются (β похоже на константу α в том, что высокое β делает более представительны­ми текущие изменения в тренде. Низкое β дает меньший вес те­кущим трендам. Значение р может быть найдено путем определе­ния ошибок и МАО, используемых как измеритель для сравнения.

Простое экспоненциальное сглаживание часто относится к сглаживанию первого порядка, а сглаживание с трендовым регу­лированием называется сглаживанием второго порядка. Другие модели экспоненциального сглаживания, включая сезонное регу­лирование и тройное сглаживание, также используются, но они не описаны в данной книге.

Трендовое проектирование. Метод прогнозирования на основе прошлых временных серий, который мы будем обсуждать, называется трендовым проектированием. Этот метод устанавливает линию тренда по серии точек прошлых данных, а затем проекти­рует линию в будущее для средне- и долгосрочных прогнозов. Ряд математических уравнений-трендов может быть использован (на­пример, экспоненциальные и квадратные), но в данной секции мы будем рассматривать только линейные (прямолинейные) тренды.

Если мы решили развивать линейный тренд линейно точным статистическим методом, то можем применить метод наименьших квадратов. Этот метод позволяет получить прямую линию, которая минимизирует сумму квадратов вертикальных разностей между линией и каждым текущим наблюдением. Рис. 4.4 иллюстрирует метод наименьших квадратов.

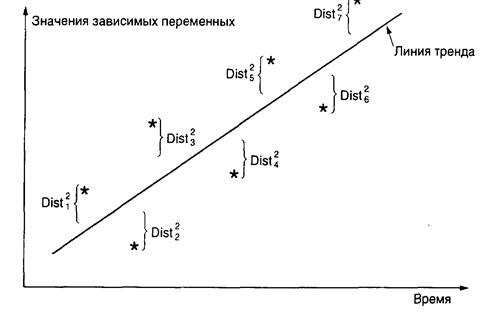
Pнс. 4.4. Метод наименьших квадратов для нахождения лучшей прямой линии (звездочки показывают семь текущих наблюдений или точек данных)

Линия, полученная методом наименьших квадратов, описыва­ется в терминах ее y-значения (высотой, отсекаемой ею на оси у) и ее наклоном (линейным углом). Если мы можем рассчитать отсекаемое y-значение и наклон, то можем описать линию следу­ющим уравнением:

y=а+bх, (4.8)

где у — расчетное значение предсказываемой переменной (зави­симой переменной);

а — отрезок, отсекаемый прямой на оси у;

b — наклон линии регрессии (или коэффициент изменения значения у по отношению к изменению значения х);

х — независимая переменная (в данном случае время).

Статистически, имея уравнение, мы можем найти значения а и b для некоторой линии регрессии. Наклон линии регрессии находим так:

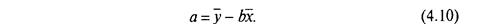
Пример 6 изображает, как использовать этот подход.