Теорема о равновесии трех сил
Теорема. Если система трех не параллельных сил, расположенных на плоскости находятся в равновесии, то их линия действия пересекаются в одной точке.
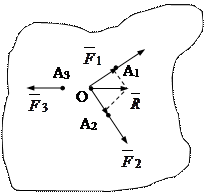 |
Рис.2.5.
Доказательство: Пусть плоская система непараллельных сил 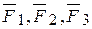 приложена в точках тела А1, А2, А3, которое находится в равновесии (рис.2.5). Тогда силы
приложена в точках тела А1, А2, А3, которое находится в равновесии (рис.2.5). Тогда силы 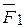 и
и 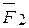 заменяем их равнодействующей
заменяем их равнодействующей  . Она приложена к точке О, т.е..
. Она приложена к точке О, т.е.. 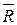 =
= 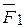 +
+ 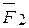 . Тогда
. Тогда
( 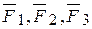 ) ~ (
) ~ ( 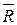 ,
, 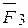 ) ~ 0.
) ~ 0.
Согласно аксиомы 1 силы 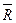 и
и 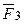 по величине равны и противоположно направлены вдоль одной прямой, проходящей через точку О. Следовательно, сила
по величине равны и противоположно направлены вдоль одной прямой, проходящей через точку О. Следовательно, сила 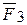 проходит через точку О.
проходит через точку О.
Ниже рассмотрим несколько несложных примеров, для решения которых применяются условия равновесия системы сходящихся сил.
Вкратце методическое указание для решения задач этой лекции сводится к следующему:
1.Устанавливается тело, для которого будет изучено условие равновесия.
2.Выбирается система координат.
3.Будут указаны активные внешние силы, действующие на тело.
4.Действие связей заменяется силами реакции.
5.Согласно уравнения равновесия будут составлены алгебраические их выражения.
6.Решив их находят неизвестные силы.
Задача 2.1. Стержни АВ и ВС соединены между собой и потолком посредством шарниров. К шарнирному болту В подвешен груз Q=1000 Н (рис.2.6).
Определить усилия в стержнях для случая, когда a=300, b=450.
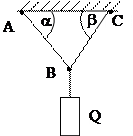 |
Рис.2.6.
Решение: Шарнир В представим как материальную точку, затем исследуем ее равновесие. К этой точке приложен груз Q.
Силы реакций стержней АВ и ВС направлены вдоль этих стержней. Их обозначим через 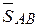 и
и 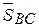 и направим их как показаны на рисунке 2.7.
и направим их как показаны на рисунке 2.7.
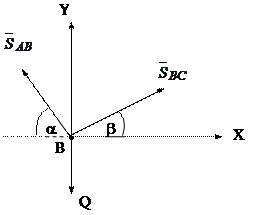 |
Рис.2.7.
В результате 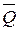 ,
, 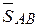 ,
, 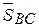 в точке В составляют систему 3-х сходящихся сил. Теперь выберем систему координат ХВУ и для данной задачи используем систему уравнений (2.10), т.е.
в точке В составляют систему 3-х сходящихся сил. Теперь выберем систему координат ХВУ и для данной задачи используем систему уравнений (2.10), т.е.
-SABcosa + SBCcosb=0
SABsina + SBCsinb - Q=0.
Первое из этих уравнений умножаем на sina, а второе - на cosa, затем обе части полученных выражений складывая, получим:
SBC(sina cosb+ cosa sinb)=Qcos a
Откуда
SBC= 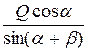
Аналогичным приемом находим:
SAB= 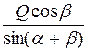
или
SBC= 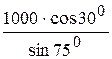 =901 Н.
=901 Н.
SAB= 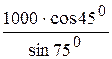
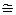 796 Н.
796 Н.
Дата добавления: 2015-02-25; просмотров: 1157;
