Некоторые понятия о равновесии в процессах сушки

Схема выпарной установки с частичным тепловым насосом показана на рис. 3.3.

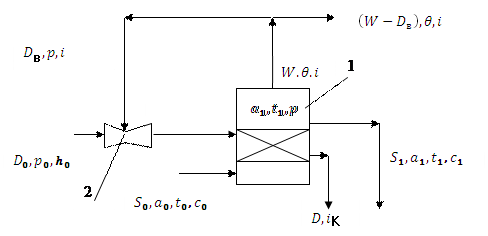Рис. 3.3. Схема выпарной установки с частичным тепловым насосом: 1 – выпарной аппарат; 2 – инжектор.

В установке с частичным тепловым насосом вторичный пар сжимается с помощью первичного греющего пара высокого давления 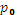в инжекторе. При этом может быть использована только часть вторичного пара 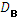, отсюда название установки.

Инжектор представляет собой устройство, состоящее из: сопла, камеры смешения, конфузора, диффузора. Пар высокого давления с высокой скоростью через сопло попадает в камеру смешения, где захватывает часть вторичного пара. Смесь первичного греющего пара со вторичным направляется на участок «конфузор – диффузор», где в конечном итоге происходит преобразование кинетической энергии потока в его потенциальную энергию давления. Основной характеристикой инжектора является коэффициент инжекции 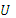, представляющий собою отношение между увлеченной частью потока вторичного пара и потоком первичного греющего пара

. (4.3)

Потребный расход греющего пара определяется формулой, ранее записанной для установки с полным тепловым насосом.

Составляя уравнение материального баланса для инжектора, получим

, (5.3)

откуда потребный расход первичного (ижектирующего) греющего пара будет равен

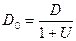. (6.3)

Коэффициент инжекции рассчитывается по определенной методике и колеблется в пределах от 0,5 до 1.

Использование такой установки экономически целесообразно при условии, если температурная депрессия кипящего раствора невелика и, следовательно, невелика степень сжатия вторичного пара в инжекторе (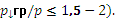

Некоторые понятия о равновесии в процессах сушки

Почти каждый твердый материал способен поглощать влагу из окружающей среды или отдавать ее окружающей среде. Направление течения процесса переноса влаги является наиболее существенным вопросом в практике сушки, так как от него зависит ее режим, т. е. условия, в которых влажный материал способен отдавать влагу окружающей среде.

Окружающий влажный материал среда содержит либо водяной пар, либо смесь водяного пара с газами. Обозначим давление водяного пара, когда только он является окружающей средой (контактная сушка), через Р₀, а парциальное давление его в смеси с газами окружающей среды (газовая сушка) Р_п.

Влаге, содержащейся в материале, соответствует определенное давление водяного пара Р_М, называемое далее давлением водяного пара во влажном высушиваемом материале.

Очевидно, что условием сушки являются неравенства

Р_М > Р₀ или Р_М > Р_п.

Давление водяного пара в высушиваемом материале Р_М зависит от влажности материала, температуры его и характера связи влаги с материалом.

С ростом влажности материала и температуры величина Р_М возрастает. С другой стороны, чем сильнее связь влаги с материалом, тем меньше, при прочих равных условиях, давление водяных паров во влажном материале.

Влажность материала, отвечающая условиям Р_М = Р₀ или Р_М = Р_п, соответствует достижению равновесия.

В последующем нами будет рассматриваться более детально только воздушная сушка.

Физические свойства влажного воздуха ( ).

Во всех сушильных аппаратах воздушной (газовой) сушки высушиваемые материалы контактируют с влажным воздухом или его смесью с топочными газами. При этом воздух отдает материалу тепло, требуемое для высушивания, и уносит испарившуюся влагу. Таким образом, воздух играет роль носителя тепла и влаги. Вот почему в первую очередь необходимо рассмотреть физические свойства влажного воздуха.

Влажный воздух считают механической смесью абсолютно сухого воздуха и смешанных с ним водяных паров. Такая смесь подчиняется закону Дальтона

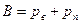, где B – полное давление влажного воздуха, p_в и p_п – парциальные давления компонентов.

Абсолютной влажностью воздуха ρ_п называют массу паров воды в 1 м³ его объема, иначе говоря, это плотность паров воды при их парциальном давлении во влажном воздухе, температура которого t_в

Предельная абсолютная влажность равна плотности сухого насыщенного пара ρ_н при той же температуре влажного воздуха t_в. Такой воздух называется насыщенным. Абсолютная влажность ненасыщенного воздуха всегда меньше абсолютной влажности насыщенного воздуха.

Относительной влажностью воздуха называют отношение выше названных величин, т.е.

.

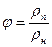Применяя к компонентам влажного воздуха уравнение состояния идеальных газов, для ненасыщенного пара можно записать

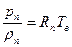, где R_п – газовая постоянная паров воды.

Для насыщенного пара

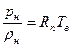. Откуда следует, что

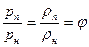
Влагосодержанием воздуха называют массу влаги, приходящуюся на 1 кг его абсолютно сухой части.

Пусть имеется объем влажного воздуха V при температуре T_в. Пусть в этом воздухе содержится G_п кг пара и G_в кг абсолютно сухого воздуха. Запишем для каждого из компонентов воздуха уравнение состояния идеального газа

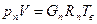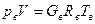, , где R_в – газовая постоянная воздуха.

Из последних уравнений следует, что влагосодержание воздуха есть

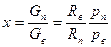, но 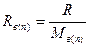, а p_в = B – p_п, где R – универсальная газовая постоянная. Тогда

, .

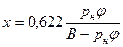Относительной энтальпией влажного воздуха называют энтальпию такой массы влажного воздуха, в котором содержится 1 кг абсолютно сухого воздуха и, следовательно, x кг водяного пара. Поэтому

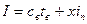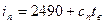[ ], где с_в – теплоемкость абсолютно сухого воздуха, i_п – энтальпия водяного пара. При этом теплоемкость абсолютно сухого воздуха может быть принята равной 1 кДж/кг град, а теплоемкость пара 1,97 кДж/кг град. Энтальпия пара может быть рассчитана по формуле , где 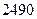- теплота испарения воды при температуре 0 ⁰С, 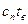- теплота нагрева водяных паров от 0 до 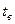⁰С

Условным удельным объемом влажного воздуха, V₀, называют такой объем влажного воздуха, в котором содержится 1 кг а.с.в.

Запишем уравнение Менделеева – Клайперона для одного из компонентов этого объема влажного воздуха, а именно, для абсолютно сухого воздуха

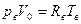, откуда 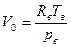. С другой стороны, парциальное давление а. с.в. может быть выражено через влагосодержание по формуле

, , .

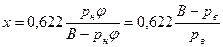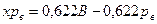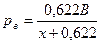В результате получим

[ ].

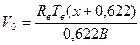Плотность влажного воздуха может быть найдена по формуле

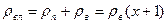, с другой стороны, после записи уравнений Менделеева – Клайперона для а. с.в. двух условий: нормальных и рабочих, получим

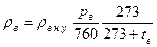, где ρ_в.н.у.=М_в/22,4; а р_в = B – р_п. Тогда

.

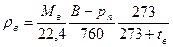Диаграмма Рамзина. Изображение процессов нагревания и охлаждения в I – x диаграмме. Точка росы. Температура точки росы.

Графический метод определения параметров влажного воздуха с помощью диаграммы Рамзина является менее трудоемким и более наглядным.

По оси абсцисс диаграммы отложены значения влагосодержания. По оси ординат – значения энтальпии. Диаграмма построена для давления 745 мм Hg. На диаграмме нанесены линии: I = const, x = const, t = const, φ = const.

Угол между осями составляет 135 ⁰, что обеспечивает наиболее комфортное использование поля диаграммы (линии постоянной относительной влажности в этом случае отстоят друг от друга в большей мере, нежели, если бы угол между осями составлял бы 90⁰).

Пусть известны начальные параметры воздуха (до нагревания): φ₀, t₀. Найдем точку пересечения соответствующих линий в поле диаграммы Рамзина (т. 0). Зная положение т. 0, определяем значения других параметров влажного воздуха: I₀, x₀ (см. рис. 2.1).

Пусть известна температура окончания процесса нагревания воздуха t₁. Так как при нагревании воздуха масса влаги в нем остается неизменной, то изменение параметров воздуха при этом будет соответствовать линии x = const от точки 0 до изотермы t₁. На пересечении линий постоянного влагосодержания и изотермы определяем положение точки 1 – окончания процесса нагревания. Зная положение т. 1, определяем значения других параметров воздуха: I₁, φ₁. Линия «0 – 1» определяет характер изменения параметров влажного воздуха в процессе его нагревания.

Аналогичным образом может быть рассмотрен процесс охлаждения воздуха (см. рис. 2.1).

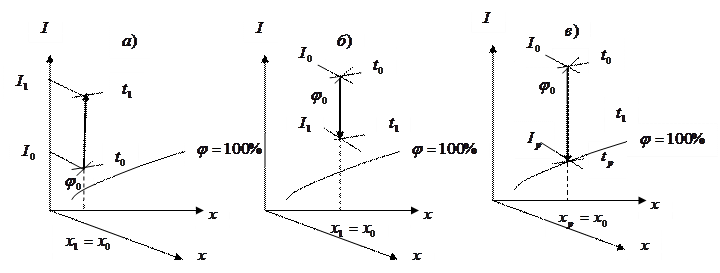
Рис. 2.1. Изображение процессов нагревания и охлаждения в диаграмме Рамзина: а) нагревание; б) охлаждение; в) определение точки росы и температуры точки росы.

Пусть известны параметры т. 0: φ₀, t₀. Требуется охладить воздух до состояния, при котором относительная влажность будет равна 100%. Проведем линию охлаждения от т. 2 до линии φ = 100% (см. рис. 2.1). Точка пересечения линии x = const с линией φ = 100% носит название точки росы. Изотерма, проходящая через точку росы, называется температурой точки росы, t_p.