Условия равновесия системы сходящихся сил

Теперь после того, как совокупность сходящихся сил, действующих на твердое тело, привелась к равнодействующей, уже можно установить ее условия равновесия.

Выше было сказано о том, что всякая система сходящихся сил имеет равнодействующую и она 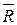~ ( 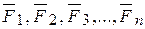). Следовательно, когда тело, на которое действует такая система сил, может находиться в равновесии? Конечно, только при условии, когда равнодействующая заданной системы сил будет равна нулю, т.е.

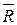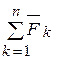= =0. (2.8)

Это выражение определяет условие равновесия и оно представлено в векторной форме. Его можно сформулировать следующим образом: для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы равнодействующая их равнялась нулю. Это условие означает, что в силовом многоугольнике конец последней силы должен совпадать с началом первой силы, т.е. силовой многоугольник в этом случае замкнут. Это положение удобно использовать, когда решение плоской задачи статики производится графическим способом.

В проекциях на прямоугольнике декартовы оси координат, т.е. в координатной (аналитической) форме, условия равновесия, согласно (2.8), представляются в виде

R_x= 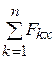=0, R_y= 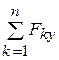=0, R_z= 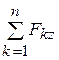=0. (2.9)

Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы одновременно сумма проекции всех сил на каждую из осей координат была равна нулю. Для частного случая, когда система сходящихся сил расположена в плоскости, например, в ОХУ, то третье условие в (2.9) обращается в тождество, т.е. необходимость его использования отпадает и условия равновесия имеют вид:

R_x= 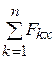=0, R_y= 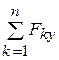=0. (2.10)

Следует отметить, что полученные условия равновесия (2.8)-(2.10) дают возможность установить, находится ли рассматриваемое твердое тело в состоянии равновесия или нет. Кроме того, они позволяют находить те или иные неизвестные, подлежащие определению по условиям исследуемой задачи. Этими неизвестными могут оказаться реакции наложенных на тело связей. Конечно, определение неизвестных искомых возможно лишь в тех случаях, когда число неизвестных не превышает числа уравнений равновесия. Следовательно, при решении задач на равновесие твердого тела, подверженного действию системы сходящихся сил, число неизвестных для пространственной задачи не должно превышать числа трех, а для плоской задачи двух, т.е. соответственно уравнениям равновесия. Если число неизвестных, подлежащих определению больше, чем уравнений равновесия, в которые они входят, то методы статики твердого тела оказываются недостаточными для их нахождения, и в этом случае исследуемая задача становится статически неопределимой. Например, к потолку подвешен груз весом Р на трех стержнях, лежащих в одной плоскости. Для определения усилия в стержнях вырезаем узел, где сходятся все стержни и действие верхних отброшенных частей заменяем неизвестными силами 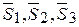(рис.2.4). Так как сила тяжести груза и указанные неизвестные усилия в стержнях составляют плоскую систему сходящихся сил, то статика для них дает всего два условия равновесия, из которых невозможно определить три искомые величины. Для составления недостающего уравнения следует рассмотреть деформацию системы, опустив узел О на некоторую малую величину, которая одновременно будет представлять собой удлинение стержней. Однако составление недостающих уравнений выходит за рамки теоретической механики и относится к курсу сопротивления материалов и строительной механики.

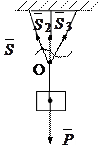Рис.2.4.