Геометрический способ решения задачи

Чтобы точка В находилась в равновесии необходимо и достаточно

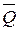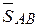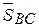+ + =0.

Это означает, что силовой треугольник построенный из сил 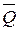, , 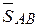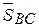должен быть замкнут. Для построения этого треугольника выберем определенный единичный масштаб. Затем известную силу 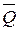параллельно самой себе переносим в любую выбранную О₁ точку пространства. После чего из точек О₁ и Е проводим прямые параллельные к стержням АВ и ВС.

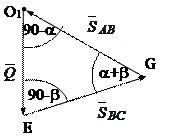Рис.2.8.

Если точку пересечения этих прямых обозначим через букву G, то полученный треугольник DO₁EG будет означать замкнутый силовой многоугольник. Причем EG и GO₁ вектора соответственно определяют силы реакци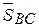и и 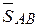. Их модули при выбранном масштабе находятся как длины EG и GO₁.

Величины 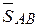и 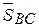можно определить и тригонометрическим путем, использовав теорему синусов, т.е.

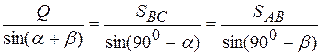
Откуда

S_BC= ,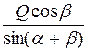

S_AB= .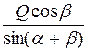

Задача 2.2.Груз Q=100 Н поддерживается брусом АО, шарнирно закрепленным в точке А и наклоненным под углом 45⁰ к горизонту, и двумя горизонтальными цепями ВО и СО одинаковой длины: ÐCBO=ÐBCO=45⁰ (рис.2.9). Найти усилие S в брусе и натяжения Т цепей.

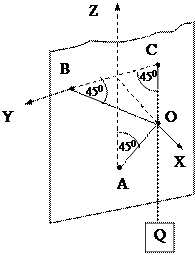Рис.2.9.

Решение. Мысленно освобождаемся от связей. Тогда точка О будет находится в равновесии под действием неизвестных сил 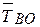, , 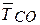S и известной 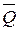(рис.2.10).

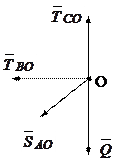Рис.2.10.

Выберем оси координат как показано на рисунке 2.9.

Составим уравнение (2.9) применительно к исследуемой задаче

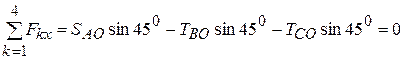
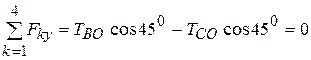
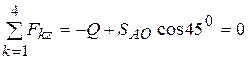
Откуда

S_AO=S= ,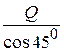

T_BO=T_CO=T,

T= .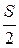

Подставив известные данные в эти выражения, находим, что

S=141,8 H, T=70,9 H.