Учебно-методические рекомендации. Проблемную ситуацию можно создать при рассмотрении вопроса о сложении сходящихся сил, приложенных к абсолютно твердому телу.

Проблемную ситуацию можно создать при рассмотрении вопроса о сложении сходящихся сил, приложенных к абсолютно твердому телу.

Здесь нужно приводить ряд рисунков и просить студентов определить на каких из них изображена система сходящихся сил. Студенты должны представить себе, что силы могут быть сходящимися, не будучи приложенными в одной точке. Они должны знать, что сходящиеся силы, приложенные в разных точках твердого тела, всегда можно перенести в одну точку – точку пересечения их линий действия.

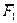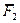Примером простейшей системы сходящихся сил является две силы, и , приложенные к одной точке абсолютно твердого тела. Равнодействующую двух этих сил находят как диагональ параллелограмма, построенного на данных векторах и можно ограничиться построением такого треугольника, называемого силовым. Для построения силового треугольника вторая сила 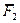как вектор переносится в конец первого вектора 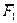и соединяется начало вектора 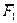с концом вектора .

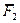В этой связи перед студентами можно поставить вопрос: можно ли переносить силу, изображенную вектором 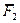параллельно ей самой не меняя ее действия на тело? Надо вместе с обучающимися вспомнить и представить из ранее сказанного о силах и аксиомах. Наверняка кто-то из студентов вспомнят школьную программу о сложении двух сил или догадываются сами как переносить силу параллельно самой себе. После такого краткого обсуждения можно дойти до истины.

Параллельный перенос вектора силы при построении треугольника является чисто графическим приемом. Этот прием позволяет обойтись без построения параллелограмма при отыскании вектора равнодействующей, но не означает, что силу можно переносить параллельно ей самой, не меняя ее действия на тело. Аналогичным образом проблемные ситуации можно создать при определении равнодействующей сходящих сил 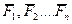. Здесь можно студентам задать вопрос: как вы думаете, зависят ли модуль и направление равнодействующей R от последовательности сложения сходящихся сил 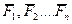. В качестве примера можно взять систему сходящихся трех 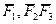сил, для которых студенты в своих тетрадях строят свой силовой многоугольник, учитывая, что сложение сходящихся сил основано на четвертой аксиоме статики – правиле параллелограмма сил.

Данный графический способ для пространственной системы сходящихся сил менее удобен, чем аналитический. При аналитическом определении равнодействующей любого числа сходящихся сил исходят из того, что проекция равнодействующей на любую декартовую ось 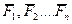соответственно равна алгебраической сумме проекций слагаемых сил. Здесь проблемную ситуацию можно создать перед обучающимися задав вопрос: как можно определить величину и направление равнодействующей, зная проекций всех сходящихся сил на декартовые оси координат 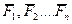? Пусть над этими вопросами студенты подумают самостоятельно, так как у них уже есть представление о векторном анализе курса математики.

Изучая условия равновесия системы сходящихся сил, можно рассматривать проблемную ситуацию с точки зрения геометрии. Студентам дать три силовых многоугольника с четырьмя и пятью силами изображенными на рисунках и задать вопрос: какой из них замкнут и как это установлено? Так же можно задать вопросы: изменятся ли уравнения равновесия, если мы изменим оси координат? Может ли равняться нулю равнодействующая трех сходящихся сил, не лежащих в данной плоскости? Как решается задача в тех случаях, когда искомые и заданные силы приложены к различным телам?

Проблемную ситуацию также можно создать при рассмотрении одного из важнейших понятий – момент силы. Момент силы характеризует вращательное воздействие на тело. Различают алгебраический и векторный моменты силы относительно точки и момент силы относительно оси. Здесь можно студентам задать вопрос: зная проекции сил на оси координат 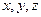и координаты точки их приложения, как можно определить вектор момента силы, относительно начала координат? Зависят ли скалярные и векторные произведения двух векторов от порядка сомножителей? Причем эти понятия студентам известны еще со школьной скамьи, т.е. из школьной программы по физике. Студентам полезно знать, когда момент силы относительно оси равен нулю? Существуют четыре случая, когда эта величина равна нулю и их должны определить сами студенты. Следует заметить, что без правильного вычисления моментов силы относительно точки и оси невозможно решить задачу, связанную с ними.

Материал данной лекции можно отнести к достаточно сложным, поэтому следует уделить больше внимания на разработку раздаточных материалов.

В качестве использования технических средств обучения можно рекомендовать раздаточный материал с демонстрацией его с помощью кодоскопа.

Можно рекомендовать использовать внутрипредметные связи при рассмотрении условия равновесия системы сходящихся сил, приложенных к абсолютно твердому телу. Фактически системы сходящихся сил является частным случаем сил, существующих в природе. Это свидетельствует о единстве и влиянии внешних сил на все процессы, происходящие на земле и природе в целом.

Профессиональная направленность материала лекции оценивается тем, что здесь рассматриваются такие задачи, которые связаны с реальным миром. Уметь их решать должен каждый обучающийся студент.

Воспитательную направленностьучебного материала можно определить путем изучения элементов статики в диалектическом развитии единства ранее рассмотренным материалом. Необходимо подчеркнуть роль казахстанских ученых в становлении и развитии теоретической механики.