Сложение двух параллельных сил
В предыдущей лекции были разобраны вопросы о сложении сил, линии действия которых пересекались в одной точке. Благодаря чему, определили их равнодействующую; установили условия равновесия для системы указанных сил. Научились вычислять моменты силы относительно произвольной точки и оси.
Теперь займемся сложением сил, линии действия которых параллельны. 1.Сложение двух параллельных сил, направленных в одну сторону. Начнем это с простейшего случая, когда на твердое тело действуют две параллельные силы F1 и F2, приложенные соответственно в точках А и В и направленные в одну и ту же сторону (рис.3.1).
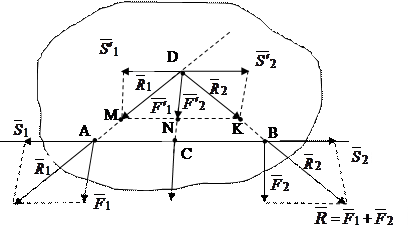 |
Рис.3.1.
Соединив прямой линией точки А и В, приложим к ним две равные по величине силы  и
и  (
(  , S2) ~ 0, направленные по прямой АВ в противоположные стороны. Такую систему двух сил, эквивалентную нуля, согласно аксиоме 3, всегда можно добавить к системе других сил или изъять из нее. Следовательно, (
, S2) ~ 0, направленные по прямой АВ в противоположные стороны. Такую систему двух сил, эквивалентную нуля, согласно аксиоме 3, всегда можно добавить к системе других сил или изъять из нее. Следовательно, ( 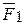 ,
, 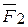 )~(
)~( 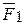 ,
, 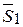 ,
, 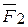 ,
, 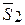 ). Далее сложив силы
). Далее сложив силы 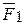 с
с 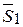 и
и 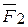 с
с 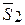 находим их равнодействующие, приложенные соответственно в точках А и В
находим их равнодействующие, приложенные соответственно в точках А и В
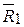 =
= 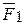 +
+ 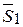 ,
, 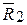 =
= 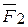 +
+ 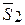 .
.
Их перенесем в D точку пересечения линии действия сил 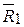 и
и 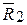 (эти вектора скользящие). Затем разложим их на составляющие
(эти вектора скользящие). Затем разложим их на составляющие 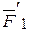 ,
, 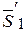 и
и 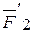 ,
, 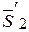 , параллельные соответственно силам:
, параллельные соответственно силам: 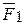 ,
, 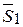 и
и 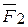 ,
, 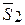 . Но
. Но 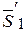 =-
=- 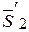 и
и 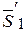 =
= 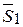 ,
, 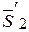 =
= 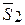 , то
, то 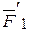 =
= 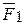 и
и 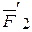 =
= 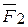 . Следовательно, две силы
. Следовательно, две силы 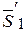 и
и 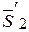 , приложенные в точке D, взаимно уравновешиваются, так как
, приложенные в точке D, взаимно уравновешиваются, так как 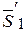 =
= 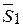 ,
, 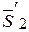 =
= 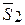 , а силы
, а силы 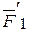 , по модулю равные соответственно F1 и F2, направлены вдоль одной прямой DC в одну и ту же сторону. Тогда складывая эти две силы получим их равнодействующую
, по модулю равные соответственно F1 и F2, направлены вдоль одной прямой DC в одну и ту же сторону. Тогда складывая эти две силы получим их равнодействующую 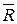 , по величине равную сумме величин F1 и F2, т.е. направленную
, по величине равную сумме величин F1 и F2, т.е. направленную 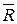 =
= 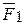 +
+ 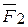 по той же прямой DC. Если продолжим линию действия силы
по той же прямой DC. Если продолжим линию действия силы 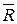 до пересечения с прямой АВ, то находим точку С, куда можно перенести силу
до пересечения с прямой АВ, то находим точку С, куда можно перенести силу 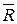 .
.
Определим положение точки С на прямой АВ. Из (подобия треугольников) DDCA~DDNM и DDCB~DDNK, имеем
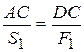 ;
; 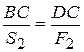 .
.
Из этих равенств, учитывая S1=S2 получим
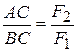 ,
,
т.е. точка С делит один отрезок АВ на части обратно пропорциональные величинам F1 и F2. Откуда F2=F1 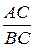 . Подставив это соотношение в F1+F2=R, получаем
. Подставив это соотношение в F1+F2=R, получаем
AC=AB 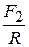 , BC=AB
, BC=AB 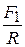 . (3.2)
. (3.2)
Таким образом, система двух параллельных сил 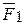 и
и 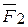 , действующих на тело и направленных в одну сторону всегда имеют равнодействующую параллельную им и по модулю она равна сумме модулей слагаемых. Причем линия действия равнодействующей делит расстояние между точками приложения сил внутренним образом на части обратно пропорциональные модулям этих сил.
, действующих на тело и направленных в одну сторону всегда имеют равнодействующую параллельную им и по модулю она равна сумме модулей слагаемых. Причем линия действия равнодействующей делит расстояние между точками приложения сил внутренним образом на части обратно пропорциональные модулям этих сил.
2.Сложение антипараллельных двух сил. Такими являются параллельные силы, направленные в противоположные стороны.
Допустим, что на твердое тело в точках А и В приложены силы 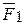 и
и 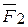 , как показано на рис.3.2.
, как показано на рис.3.2.

Рис.3.2.
Причем F1>F2. Для данного случая требуется определить равнодействующую сил 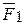 и
и 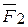 . Для этого силу
. Для этого силу 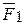 (большую) разложим на две параллельные силы, одна из которых
(большую) разложим на две параллельные силы, одна из которых 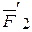 приложена в точке В и равна по модулю силе F2. Тогда модуль второй составляющей равен R=F1-F2=F1-
приложена в точке В и равна по модулю силе F2. Тогда модуль второй составляющей равен R=F1-F2=F1- 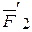 и ее линия действия должна проходить через точку С, лежащую на продолжении прямой АВ, как показано на рис.3.2. Здесь исходная систем сил (
и ее линия действия должна проходить через точку С, лежащую на продолжении прямой АВ, как показано на рис.3.2. Здесь исходная систем сил ( 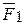 ,
, 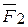 ) заменена эквивалентной системой (
) заменена эквивалентной системой ( 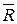 ,
, 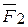 ,
, 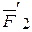 ). Однако силы
). Однако силы 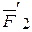 и
и 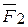 взаимно уравновешиваются, следовательно их можно отбросить. В результате две неравные силы (
взаимно уравновешиваются, следовательно их можно отбросить. В результате две неравные силы ( 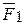 ,
, 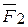 ), направленные в противоположные стороны заменены одной силой
), направленные в противоположные стороны заменены одной силой 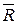 =
= 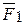 -
- 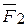 . При этом отрезок АС должен удовлетворять пропорции:
. При этом отрезок АС должен удовлетворять пропорции:
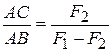 или
или 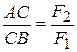 . (3.3)
. (3.3)
Таким образом, система двух неравных антипараллельных сил 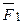 и
и 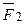 всегда имеет равнодействующую
всегда имеет равнодействующую 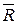 , параллельную этим силам, причем ее модуль равен разности модулей слагаемых и линия действия равнодействующей делит расстояние между точками приложения слагаемых сил внешним образом на части, обратно пропорциональные модулям этих сил и расположена за большей из двух сил.
, параллельную этим силам, причем ее модуль равен разности модулей слагаемых и линия действия равнодействующей делит расстояние между точками приложения слагаемых сил внешним образом на части, обратно пропорциональные модулям этих сил и расположена за большей из двух сил.
Рассмотрим теперь случай двух параллельных и равных по модулю, но противоположно направленных сил, т.е. как быть если F1=F2?
Дата добавления: 2015-02-25; просмотров: 1870;
