Система сходящихся сил

Совокупность системы сил, линии действия которых пересекаются в одной точке О, называется сходящейся. Пусть такая система сил ( 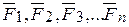) приложена к некоторому абсолютно твердому телу в точках А₁, А₂, …,А_n (рис.2.1).

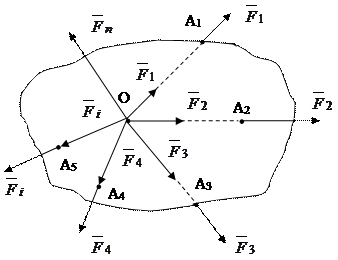Рис.2.1.

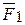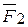Согласно свойству абсолютно твердого тела силы могут быть перенесены вдоль линии действия в точку О, ибо все они являются скользящими векторами. В дальнейшем данную систему сил следует привести к простейшему виду, так как заранее о действии этой системы, оказываемой на тело что-либо сказать трудно. Для этого будет складывать заданные силы последовательно. В начале сложим силы и . При этом, использовав аксиому параллелограмма, находим их равнодействующую 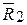= 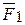+ 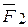. Затем, складывая силы 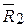и 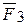, т.е., использовав опять правило параллелограмма, определим их равнодействующую 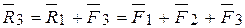. Этот прием, продолжая дальше и наконец, складывая силы 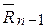и 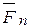, находим такую силу, которая и является искомой равнодействующей всех заданных сил. Построение этой равнодействующей может быть упрощено, если вместо параллелограммов построить силовой многоугольник. Для этого, чтобы найти равнодействующую сил 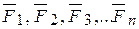достаточно произвести следующее построение. Из произвольной точки О₁, выбрав определенный масштаб, откладываем вектор 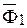, геометрически равный 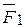, т.е. равный по величине и направленный по направлению этой силе. Теперь из конца этого вектора откладываем 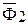, геометрически равный 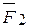. 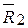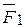Соединив О₁ с концом этого вектора, находим вектор, геометрически равный равнодействующей сил и 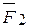. Построение такого треугольника полностью определяет вектор 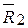. Продолжая построение, отложим вектор 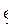геометрически равный 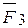, помещая его начало в конце вектора 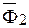. Тогда вектор, соединяющий начало О₁ и конец вектора 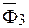дает равнодействующую 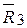. Далее снова с конца вектора 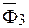отложим вектор 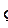, геометрически равный 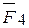. При этом вектор 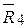, соединяющий точку О₁ с концом вектора 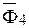дает не что иное как равнодействующую 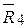, равную геометрической сумме сил 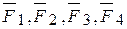. Продолжая подобным образом, сложим сколько угодно сил и получим вектор, геометрически равный равнодействующей 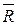заданной системы сил. Следовательно, для любой системы сходящихся сил определение их равнодействующей не представляет трудностей, если отложив на диаграмме вектор 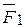, к концу его приложить начало вектора 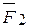, затем к концу 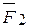- начало вектора 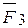, к концу 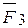-начало 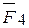и т.д. до тех пор, пока не будут приложены все заданные силы. Затем начало О₁ первого вектора соединим вектором 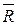с концом последнего вектора 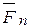, направив 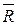навстречу силе 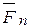. Проделав это, получим замкнутый многоугольник, который называется многоугольником сил. При этом вектор 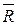, замыкающий многоугольник сил дает как величину, так и направление равнодействующей 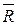заданных сил (рис.2.2).

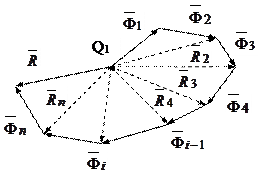Рис.2.2.

Изложенное правило построение равнодействующей 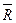называется правилом многоугольника сил. Здесь стоит обратить внимание на правило стрелок в многоугольнике сил, где все силы 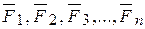обычно называемые составляющими направлены в одну сторону по обводу многоугольника, а равнодействующая 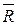направлена в противоположную сторону. Причем вектор 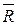называется замыкающим, который является равнодействующей всех сил. Таким образом, равнодействующая сходящихся сил равна их геометрической сумме и она будет приложена в точке пересечения линий действия сил, т.е.

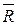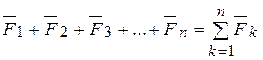= . (2.1)

Если выберем определенную систему координат, например, декартовую и начало ее поместим в точку пересечения линий действия сил, то согласно формулы (2.1) проекции равнодействующей на прямоугольные декартовые оси координат равны суммам проекций всех сил на эти же оси, т.е.

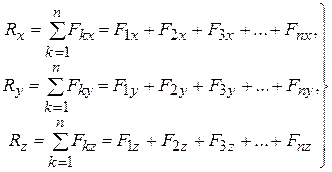, (2.2)

где F_kz, F_ky, F_kz-проекции силы 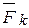на указанные оси, а R_x, R_y и R_z -проекции равнодействующей 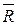на те же оси.

Итак, с помощью выражений (2.2) можно найти модуль равнодействующей в прямоугольной декартовой системе координат ОХУZ. Действительно, если иметь в виду, что составляющие равнодействующей 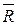системы сходящихся сил 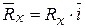, , 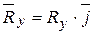, 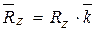где i,j,k - единичные вектора, определяющие положительные направления осей координат соответственно ОХ, ОУ, ОZ, взаимно перпендикулярны (рис.2.3), то модуль равнодействующей определяется из следующей формулы:

R= 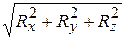, (2.3)

где R_x, R_y, R_z находятся из (2.2).

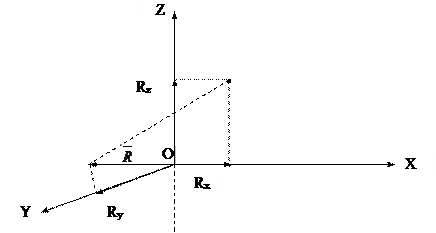Рис.2.3.

Так как равнодействующая системы сходящихся сил является векторной величиной, следовательно, необходимо указать ее направление в пространстве. Для этого воспользуемся формулами, приведенными в курсе векторной алгебры, согласно которых направляющие косинусы равнодействующей соответственно будут равны

cos( 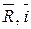)= 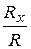, cos( 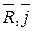)= 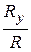, cos( 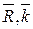)= 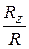. (2.4)

Следует отметить, что количество этих формул сократится, если силы, действующие на тело, расположены в одной плоскости.

Плоская система сходящихся сил. Пусть к абсолютно твердому телу приложена плоская система сходящихся сил, т.е. все силы расположены в некоторой плоскости, а их линии действия пересекаются в одной точке. Этот случай является частным случаем выше рассмотренных сил, и следовательно, для определения равнодействующей плоской системы сходящихся сил можно использовать выражения (2.2)-(2.4). Для этого удобно выбрать систему координат ОХУ в плоскости расположенных сил. Тогда проекции всех сил на ось OZ равны нулю и вместо формул (2.2), (2.3), (2.4) будет иметь

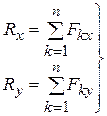(2.5)

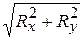R= (2.6)

cos( 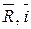)= 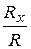, cos( 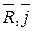)= 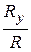, (2.7)

где R_x и R_y находятся из первых двух выражений формулы (2.2).

Итак выражения (2.5)-(2.7) дают возможность вычислить числовое значение равнодействующей заданной плоской системы сходящихся сил и указать ее направление в плоскости. В целом, определение равнодействующей сходящихся сил при помощи формул (2.1)-(2.7) является аналитическим методом. В то же время непосредственное использование многоугольника сил для решения задач статики приводит к геометрическим построениям. Этот способ в отличие от аналитического метода, указанного выше называется геометрическим. Причем для некоторых классов сходящихся сил построение силового многоугольника, для определения их равнодействующей, может быть осуществлено чисто графически. Для этого необходимо следить только затем, чтобы в принятом масштабе векторы на диаграмме достаточно изображали заданные силы. При этом длина вектора-замыкающего многоугольника дает числовое значение равнодействующей. Конечно, в случае пространственной системы сил указанное графическое построение непосредственно невыполнимо. В этом случае, чтобы определить равнодействующую, необходимо использовать аналитический метод, изложенный выше.