Теоретическая механика – наука и ее значение в естествознании.

Теоретическая механика является одной из основных естественных наук, в которых изучаются общие законы механического движения и взаимодействия материи. Здесь под материей подразумевается все то, что реально существует вне нашего сознания и независимо от него. Ее мы познаем через наши ощущения и действия. Материя вечна, неуничтожима и находится в состоянии непрерывного движения. Под движением материи понимаем все изменения и процессы, происходящие в природе. Среди многообразных ее форм движения простейшей является механическая форма движения. Таким движением называется изменение с течением времени взаимного положения тел в пространстве. Разновидностями механического движения есть движения людей и животных, автомобилей и поездов, частей машин и приборов, небесных тел, жидкостей и газов и т.д.

Конечно, в чистом виде механическое движение не существует. Оно обязательно сопровождается другими видами движения материи. Всем нам известно, что мир не остается неизменным. В нем непрерывно происходят самые различные изменения. Все вещества, создающие материю, при разных условиях могут становиться твердыми, жидкими и газообразными. Происходят химические превращения одних веществ в другие. Одним словом существуют процессы, в которых одинаковое значение с механическими имеют электрические, тепловые, химические и другие явления. Однако в преобладающем большинстве механических задач можно будет не учитывать влияния изменений других качественных признаков тела (например, его цвета, структуры, химического состава, оптических, тепловых, магнитных и других свойств) на закономерности изучаемого механического движения. Так, например, изучая явление приливных волн, нет нужды принимать во внимание содержание иода в морской воде, так как незначительные изменения процентного содержания этого химического элемента в воде не оказывают заметного влияния на механизм явления приливных волн. Но существуют в природе и такие процессы, в которых можно обнаружить, что механическое движение играет второстепенную роль. Например: действие парового котла, химического реактора, жизнедеятельность организма и т.д. В этих процессах основное значение имеет соответственно тепловое, химическое и биологическое явления.

Таким образом, механическое движение есть простейшая форма движения, представляющая изменение положения материального тела в пространстве с течением времени. А теоретическая механика есть наука об общих законах этой простейшей формы движения реальных тел. Законам механических явлений подчиняются не только тела, окружающие нас на Земле, им подчиняются в своих движениях звезды и галактики, даже самые маленькие невидимые частицы вещества - атомы и их составные части.

В настоящее время механика представляет собой целый комплекс дисциплин. Она достигла своего современного состояния и продолжает развиваться благодаря труду очень большого числа людей. Не полный перечень дисциплин, из которых состоит Механика, приведен в данной схеме.

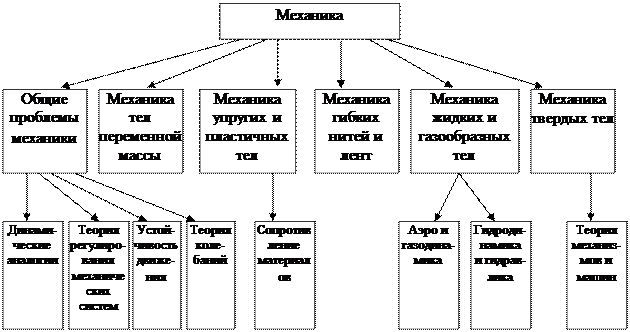
Среди них рабочие и инженеры, применяющие механическое движение в производстве: ученые-теоретики, исследующие законы механики; специалисты по методам и средствам измерения параметров механического движения.

В настоящее время ни один человек не в состоянии изучить всю механику. Для того, чтобы решить, какие разделы механики выбрать для изучения, нужно представить, для чего механика бывает нужна инженеру.

Какие механические проблемы имеют важное практическое значение? Например, при ремонте зданий, машин и приборов возникают механические проблемы, связанные с заменой изношенных или сломанных частей и последующей наладкой, т.е. механика нужна инженеру. Чем лучше он будет знать механику, тем успешнее работает.

Инженеру, работающему в цехе, конструкторском бюро или технологическом отделе, приходится сталкиваться с механическими проблемами. Бывает и так, что инженеру приходится проводить теоретические исследования механических явлений. Бывает так, что в создании механических конструкций принимают участие и ученые теоретики. Поэтому инженер должен знать механику в объеме, достаточном для того, чтобы успешно выполнять свои функции и быть в состоянии навести справки в литературе.

Законы механики нужны инженеру в качестве руководства к действию.

Теоретическая механика состоит из 3-х разделов. К ним относятся: статика, кинематика и динамика.

В статике изучается относительный покой тела. Здесь силы, действующие на тело, приводятся к простейшей системе. После чего находятся условия его равновесия.

Кинематика изучает движение материальной точки и механической системы только с точки зрения геометрии. Здесь сила не учитывается, которая вызывает то или иное движение.

В динамике, наоборот, эти силы принимаются во внимание.

Основные понятия и аксиомы статики

В каждой области знаний существует набор основных принципов (законов, аксиом). Все остальные утверждения выводятся из этих законов. Конечно, то, что очевидно для одного человека, может оказаться весьма сомнительным для другого. История всякой науки состоит в постоянном поиске более фундаментальных законов (принципов), лежащих в основе этой науки и они должны быть настолько универсальны, что ни у кого не должны вызывать сомнений. Безусловно, эти законы должны подтверждаться фактами, которые являются источником существования и развития науки. Причем теоретические выводы и положения проверяются и уточняются на практике.

Одним и основных понятий в механике является сила и масса, связанные между собой определенными соотношениями. Эти соотношения устанавливаются аксиомами и основными законами, которые кладутся в основу механики. Наиболее распространенной является классическая система таких аксиом, опубликованная в 1687 году И.Ньютоном в своем труде "Математические начала натуральной философии". Эти аксиомы (законы) применительно к статике могут быть изложены в виде положений, устанавливающих основные свойства сил, приложенных к материальной точке и абсолютно твердому телу.

Исследуя законы механического движения, теоретическая механика пользуется рядом таких отвлеченных понятий. Причем материальной точкой здесь называется тело (частица), размером которого можно пренебречь, а абсолютно твердым телом называют тело, не изменяющее своей формы под действием приложенных к нему сил.

Результаты опытов показывают, что сила приложения являясь количественной мерой механического взаимодействия тел, характеризуется величиной, направлением и точкой. Такому определению силы полностью отвечает образ вектора, равного по длине величине силы, приложенного в данной точке и направленного в сторону действия силы.

Силы, возникающие при непосредственном контакте тел, называют силами соприкосновения. Например, сила сопротивления, возникающая при соприкосновении подводной лодки с водой. В то же время взаимодействие сил на расстоянии называются дальнодействующими силами. Например, электромагнитные и гравитационные силы. Сила, приложенная к абсолютно твердому телу в одной точке, называется сосредоточенной, а действующая вдоль линии, по поверхности или объему называется распределенной. Силы обычно обозначаются большой буквой латинского алфавита с черточкой на верху, которая означает, что эта величина векторная, т.е. 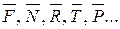. Если на тело действуют n сил, то их можно обозначить так: 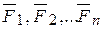и называть системой сил.

Совокупность всех сил, приложенных к одному и тому же телу, называется системой сил. Уравновешенной системой сил называется такая система, которая не нарушает равновесия тела. Системы сил, производящие одинаковое действие на одно и то же тело, называется эквивалентными. Сила, эквивалентная данной системе сил, называется равнодействующей этой системы. Причем прямая, вдоль которой расположен вектор силы, называется линией действия силы. Точку приложения силы к телу можно переносить вдоль линии действия силы лишь в том случае, если тело абсолютно твердое. Поэтому вектор силы, приложенной к абсолютно твердому телу, называют скользящим вектором. Сейчас в Международной системе единиц СИ за единицу силы принят 1 ньютон (Н) - 0,102 кГ.

Аксиома 1 (закон инерции).Действием уравновешенной системы сил материальная точка находится в покое или движется прямолинейно и равномерно. Этот закон также называется принципом инерции. Он был открыт Галилеем. Галилео Галилей родился 15 февраля 1564 г. в Пизе в семье торговца. Окончил Пизанский университет. С раннего возраста и до конца своей жизни (1642) занимался вопросами математики и механики. Сам И.Ньютон называл его предшественником в деле установления некоторых законов механики.

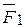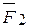Аксиома 2 (закон равновесия двух сил). Под действием двух сил свободное абсолютно твердое тело будет находиться в равновесии только в том случае, если они по величине равны и противоположно направлены по прямой, соединяющей их точки приложения (рис.1.1). Допустим, что к твердому телу приложены две силы и (рис.1.1). Безусловно, эти силы взаимно уравновешиваются только в том случае, когда они действуют по одной прямой и если 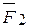=- 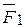. Основываясь на аксиому 2, легко доказать, что, не нарушая равновесия твердого тела, точку приложения силы можно переносить вдоль прямой, по которой направлена сила.

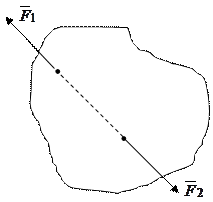Рис.1.1.

Для этого положим, что в точке А приложена сила 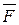. Затем возьмем на линии действия силы произвольную точку, и не нарушая состояния тела, к этой точке приложим две силы 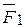и 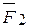, равные по модулю силе 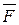. и противоположно направленные вдоль прямой, по которой действует эта сила (рис.1.2). При этом получим совокупность трех сил ( 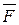, , 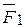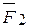). Система двух сил ( 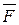, 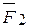), согласно аксиомы 2, не может изменить состояние данного тела. Тогда останется сила 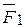, равная по величине и одинаково направленная с силой 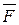, но уже имеющая другую точку приложения В. Следовательно, в абсолютно твердом теле сила является скользящим вектором и ее можно переносить в любую точку вдоль прямой, по которой действует сила.

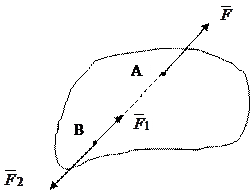Рис.1.2.

Аксиома 3. (Закон присоединения и исключения уравновешивающихся сил).Добавление или изъятие взаимно уравновешенной системы сил не нарушает прежнее состояние твердого тела.

Положим, что некоторое твердое тело находится в состоянии равновесия под действием приложенных к нему системы сил ( 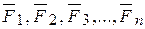). Далее присоединим к ним взаимно уравновешенную систему сил ( 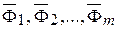), т.е. теперь имеем, что

~ ( , )

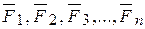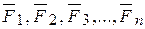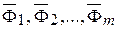Но эта система сил не может нарушить состояние равновесия исследуемого тела. Точно также можно из системы сил, приложенных к твердому телу, отбросить группу сил, взаимно уравновешивающихся.

Эту аксиому с успехом можно применить для доказательства, что равновесие твердого тела не нарушается от перенесения точки приложения силы вдоль ее линии действия в любую точку тела.

Аксиома 4. (Закон параллелограмма сил). Система двух сил, действующая на твердое тело в одной точке всегда имеет равнодействующую, приложенную в этой же точке, и изображается диагонально параллелограмма, построенного на этих силах. Допустим, что в точке О твердого тела приложена система двух сил 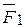и 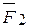(рис.1.3).

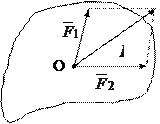Рис.1.3.

Тогда аксиома устанавливает, что ( 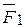, 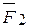)~ 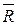и полностью определяет модуль, точку приложения и направление равнодействующей силы

= + .

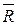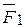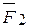Следовательно, равнодействующую 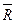можно построить как диагональ параллелограмма со сторонами с 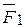и 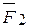. При этом модуль этой равнодействующей находится равенством

R= ,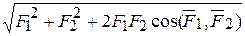

где ( 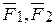)-угол между направлениями сил 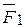и .

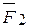Аксиома 4 дает возможность разложить любую силу 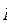на две (в плоскости), на три (в пространстве) составляющие, т.е. перейти к другой системе сил, для которой 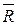является равнодействующей.

Аксиома 5. (Закон равенства действия и противодействия). Всякое действие одного тела на другое вызывает равное и противоположное направленное противодействие. Если тело А₁ действует на тело А₂ с силой 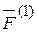, то тело А₂ на А_1­ действует с силой 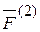, причем:

= -

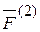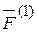
т.е. данная аксиома утверждает, что числовые значения сил действия двух тел друг на друга равны и противоположно направлены вдоль одной прямой. Следовательно, в природе не существует одностороннего действия силы. Однако эти силы приложены к различным телам и не составляют уравновешенную систему сил.

Эта аксиома установлена И.Ньютоном и является одним из основных законов классической механики.

Аксиома 6. (Закон твердения). Если деформируемое тело находится в состоянии покоя, то при мгновенном его затвердевании равновесие тела не нарушается.

Данная аксиома считает, что условия равновесия сил, приложенных к абсолютно твердому телу, должны выполняться и для сил, приложенных к деформирующему телу.

Однако для нетвердых тел (ремень, цепь, нить и др.) эти условия являются лишь необходимыми, но не достаточными.

Например, две уравновешивающиеся силы, приложенные к невесомой нити, хотя удовлетворяют условиям равновесия, но они не достаточны. Здесь необходимо дополнительно еще потребовать, чтобы эти силы были обязательно растягивающими.