I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Механизм синхронизации помогает в решении многих проблем, однако, если вы откажетесь от его использования, сразу несколько потоков смогут одновременно изменять значение некоторого поля. Если это делается намеренно (может быть, для синхронизации доступа используются другие средства), следует объявить поле с ключевым словом volatile. Например, если у вас имеется переменная, значение которой постоянно отображается потоком графического вывода и может изменяться несинхронизированными методами, то фрагмент вывода может выглядеть следующим образом:
currentValue = 5;
for (;;) {
display.showValue(currentValue);
Thread.sleep(1000); // подождать 1 секунду
}
Если бы значение currentValue не могло изменяться внутри метода ShowValue, то компилятор мог бы предположить, что величина currentValue остается в цикле постоянной, и просто использовать константу 5 вместо вызова showValue.
Однако, если во время выполнения цикла значение currentValue может быть изменено другим потоком, то предположение компилятора будет неверным. Объявление поля currentValue с ключевым словом volatile не позволяет компилятору делать подобные предположения.
ТОК В ВАКУУМЕ
I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Как известно, в металлах имеются электроны проводимости, участвующие в тепловом движении. Для вырывания электрона из металла нужно совершить определённую работу Авых, называемую работой выхода
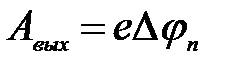 , (1)
, (1)
где е - заряд электрона;
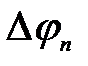 - поверхностная разность потенциалов.
- поверхностная разность потенциалов.
Так как электроны удерживаются внутри металла, то значит, вблизи поверхности существуют силы, действующие на электроны и направленные внутрь металла. Происхождение этих сил можно объяснить, во-первых, притяжением между электронами и положительными ионами кристаллической решетки; во-вторых, тем, что в результате теплового движения некоторые из свободных электронов могут выйти за поверхность металла, образуя электронное облако, которое препятствует их дальнейшему выходу.
При комнатных температурах (Т=293 К) лишь ничтожная часть электронов внутри металла имеет достаточный запас кинетической энергии, чтобы, совершив работу выхода Авых, вырваться наружу. Однако электронам можно сообщить различными способами дополнительную энергию. В этом случае часть электронов металла получает возможность покинуть металл, и мы наблюдаем явление испускания электронов, или электронную эмиссию.
В зависимости от того, каким способом электронам сообщена энергия, мы
различаем разные типы электронной эмиссии:
а) термоэлектронная эмиссия: за счёт тепловой энергии при повышении температуры тела;
б) фотоэмиссия: подвод энергии светом;
в) вторичная электронная эмиссия: при бомбардировке извне какими-либо другими частицами (электронами, ионами).
1.1. Термоэлектронная эмиссия
По мере повышения температуры эмиттера число быстрых электронов возрастает и благодаря этому должно возрастать и число электронов, вырывающихся из металла. При достаточно высокой температуре наступает заметное испускание электронов металлом. Это явление носит название термоэлектронной эмиссии.
С точки зрения классической электронной теории металл могут покинуть лишь те электроны, кинетическая энергия которых 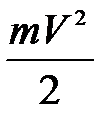 не меньше работы выхода Авых, т.е. те, для которых выполняется условие
не меньше работы выхода Авых, т.е. те, для которых выполняется условие
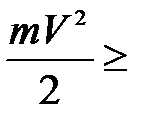 Авых или
Авых или 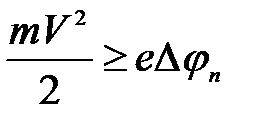 (2)
(2)
Для оценки энергии 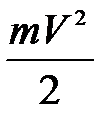 сравним её со средней энергией теплового движения атомов (или молекул), которая по классической теории равна
сравним её со средней энергией теплового движения атомов (или молекул), которая по классической теории равна 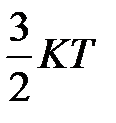 ,
,
где К - постоянная Больцмана;
Т - абсолютная температура тела.
Приравнивая тепловую энергию движения 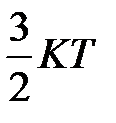 работе выхода
работе выхода
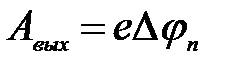 , найдём ту температуру Т, при которой средняя энергия частиц равна работе выхода
, найдём ту температуру Т, при которой средняя энергия частиц равна работе выхода
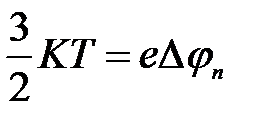 , откуда
, откуда 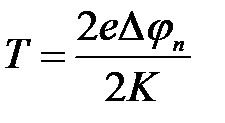 (3)
(3)
Для различных металлов работа выхода колеблется в пределах от 1 до
4,5 эВ. Если примем 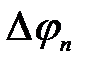 = 2В, то получим
= 2В, то получим
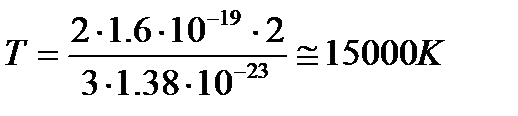 ,
,
т.е. энергия электронов, необходимая для того, чтобы они могли вылететь из металла, должна быть относительно очень велика и соответствовать средним энергиям теплового движения атомов при температурах порядка десятка тысяч градусов. На самом деле электроны начинают вылетать в заметном количестве при температурах порядка (1000–3000) К, т.е. при гораздо более низких температурах.
Это объясняется тем, что электроны имеют определённое распределение по энергиям. Благодаря этому часть электронов обладает энергиями, значительно большими, чем средняя. За счёт этих электронов и начинается термоэлектронная эмиссия.
Распределение потенциальной энергии электрона для ограниченного металла показано на энергетической диаграмме рис.1:
| П П П0 П1 Е0 | Aвых F |
Рис.1.
Здесь П0 - уровень энергии покоящегося электрона вне металла;
Е0 -наименьшая энергия электронов проводимости (дно зоны проводимости);
F - уровень Ферми.
Распределение потенциальной энергии имеет вид потенциальной ямы.
Если электрон внутри металла имеет полную энергию П1 < П0 , то такой электрон не сможет покинуть металл. Условие вылета электрона из металла:
B Z3gG2Kswo/eKBbCaE7YebEeE7G1ILpXHgx4N/Hy3gqp+zOP5eraepaN0PF2P0rgsR/ebVTqabpLb rJyUq1WZ/PSlJWleC8a48tWdFJ6kf6egYdZ6bZ41fsXiiuwmPC/JRtdlhJMFLqd3YBfU5AXUK26r 2TOIyeh+ZOGKAaPW5jtGHYxrge23PTEcI/lOwTzMkzT18x02aXY7ho259GwvPURRgCqww6g3V66/ E/atEbsaMiXhWJX2w1AJd1J7X9UgfRjJwGC4PvzMX+5D1O9LbvkLAAD//wMAUEsDBBQABgAIAAAA IQDgUoPV4gAAAAoBAAAPAAAAZHJzL2Rvd25yZXYueG1sTI/LTsNADEX3SPzDyEhsEJ08KIWQSYWQ KkEXoJbH2k1MEjXjCZlpG/r1mBUsbR9dn5vPR9upPQ2+dWwgnkSgiEtXtVwbeHtdXN6A8gG5ws4x GfgmD/Pi9CTHrHIHXtF+HWolIewzNNCE0Gda+7Ihi37iemK5fbrBYpBxqHU14EHCbaeTKLrWFluW Dw329NBQuV3vrIHwHj+X49F94eLpI3qML5arl+3SmPOz8f4OVKAx/MHwqy/qUIjTxu248qozkMaz RFADV+kUlABpciuLjZDJbAq6yPX/CsUPAAAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEB AAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9 If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhALli TkWAAgAALAUAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAh AOBSg9XiAAAACgEAAA8AAAAAAAAAAAAAAAAA2gQAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAE APMAAADpBQAAAAA= "/>
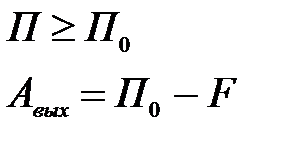 (4)
(4)
Термоэлектронная эмиссия лежит в основе получения электрического тока в вакууме и устройства вакуумных электронных ламп.
1.2.Ток в вакууме. Вольт-амперная характеристика анода. Закон Богуславского-Ленгмюра
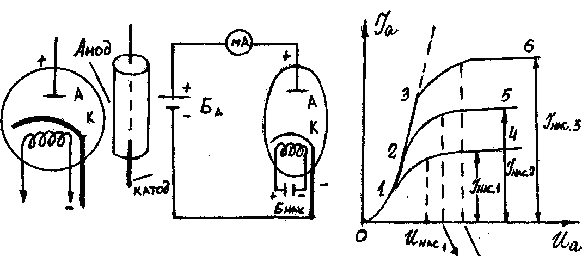
Для наблюдения термоэлектронной эмиссии может служить вакуумная электронная лампа (диод), состоящая из стеклянного баллона, из которого выкачан воздух до давления порядка 10-8 мм рт. ст., и впаянных в баллон двух металлических электродов: катода К в виде тонкой проволоки из тугоплавкого металла (вольфрам, молибден и др.) и анода, выполненного обычно в форме цилиндра (рис.2а):
|
| Uнас2 Uнас3 |
| а) б) в) |
Рис.2
Если составить электрическую цепь (рис.2б), содержащую вакуумный диод, анодную батарею Ба, батарею накала Бнак и миллиамперметр  , то при холодном катоде ток в цепи не возникает, так как сильно разреженный газ (вакуум) внутри диода не содержит заряженных частиц и потому электропроводность диода практически равна нулю. Если же катод К, соединённый с отрицательным полюсом анодной батареи Ба, раскалить при помощи добавочной батареи накала Бнак до высокой температуры, то миллиамперметр обнаруживает появление тока в цепи диода.
, то при холодном катоде ток в цепи не возникает, так как сильно разреженный газ (вакуум) внутри диода не содержит заряженных частиц и потому электропроводность диода практически равна нулю. Если же катод К, соединённый с отрицательным полюсом анодной батареи Ба, раскалить при помощи добавочной батареи накала Бнак до высокой температуры, то миллиамперметр обнаруживает появление тока в цепи диода.
Электроны, вылетающие из раскалённого катода в результате явления термоэлектронной эмиссии и образующие электронное "облако" вблизи поверхности катода, ускоряются внешним электрическим полем, создаваемым между анодом и катодом, попадают на анод и замыкают цепь диода. Через лампу идёт ток 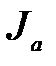 , называемый анодным.
, называемый анодным.
Ток в цепи диода появляется в том случае, если положительный полюс анодной батареи соединён с анодом, а отрицательный - с катодом. Если же изменить знак разности потенциалов 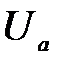 , приложенной к диоду, то тока в цепи не будет, как бы сильно мы ни раскаляли катод. Это обстоятельство показывает, что катод испускает отрицательные частицы, т.е. электроны, и что положительные ионы не покидают металл в заметном количестве.
, приложенной к диоду, то тока в цепи не будет, как бы сильно мы ни раскаляли катод. Это обстоятельство показывает, что катод испускает отрицательные частицы, т.е. электроны, и что положительные ионы не покидают металл в заметном количестве.
Сила анодного тока 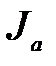 в диоде зависит от величины разности потенциалов
в диоде зависит от величины разности потенциалов 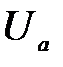 между анодом и катодом. При постоянной температуре катода ток
между анодом и катодом. При постоянной температуре катода ток 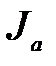 возрастает с увеличением
возрастает с увеличением 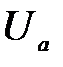 , однако зависимость между силой тока
, однако зависимость между силой тока 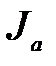 и разностью потенциалов
и разностью потенциалов 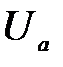 не выражается законом, аналогичным закону Ома, по которому
не выражается законом, аналогичным закону Ома, по которому  пропорционально U . Эта зависимость
пропорционально U . Эта зависимость 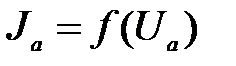 , получившая название вольт-амперной характеристики диода, носит более сложный характер, графически представленный кривой 014 (см. рис.2в). Когда
, получившая название вольт-амперной характеристики диода, носит более сложный характер, графически представленный кривой 014 (см. рис.2в). Когда 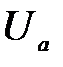 = 0, сила тока
= 0, сила тока 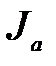 также практически равна нулю. При увеличении
также практически равна нулю. При увеличении 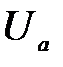 сила тока
сила тока 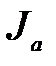 возрастает в соответствии с кривой 01. При дальнейшем возрастании анодного напряжения
возрастает в соответствии с кривой 01. При дальнейшем возрастании анодного напряжения 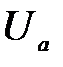 сила тока достигает некоторого максимального значения
сила тока достигает некоторого максимального значения 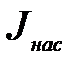 , называемого током насыщения диода, и почти перестаёт зависеть от анодного напряжения
, называемого током насыщения диода, и почти перестаёт зависеть от анодного напряжения 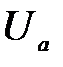 (участок вольтамперной характеристики 14).
(участок вольтамперной характеристики 14).
При увеличении температуры катода вольт-амперная характеристика изображается кривыми 0125, 01236 и т.д. При значениях тока, меньших 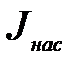 , зависимость
, зависимость 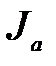 от напряжения
от напряжения 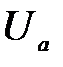 при всех температурах изображается одной и той же кривой 0123. Различными при различных температурах оказываются значения тока насыщения
при всех температурах изображается одной и той же кривой 0123. Различными при различных температурах оказываются значения тока насыщения 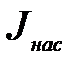 , которые быстро увеличиваются при возрастании температуры катода. При этом увеличивается и то анодное напряжение
, которые быстро увеличиваются при возрастании температуры катода. При этом увеличивается и то анодное напряжение 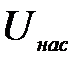 , при котором устанавливается ток насыщения
, при котором устанавливается ток насыщения 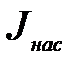 .
.
Мы видим, что вольт-амперная характеристика электронной лампы оказывается нелинейной, а следовательно, диод представляет собой пример проводника, не подчиняющегося закону Ома.
Зависимость тока диода от напряжения между анодом и катодом имеет простое объяснение. При 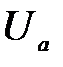 = 0 сила анодного тока
= 0 сила анодного тока 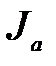 , при достаточно большом расстоянии между электродами, тоже равна нулю. Это происходит оттого, что вылетевшие из катода электроны образуют вблизи него электронное облако. Это приводит к созданию поля, которое тормозит вновь вылетающие электроны. В результате дальнейшая эмиссия электронов прекращается: сколько электронов вылетает из металла, столько же в него возвращается под действием обратного поля электронного облака. Если же между электродами создать внешнее электрическое поле, подсоединив анод А к “+”, а катод К к "-" анодной батареи Ба, то это внешнее электрическое поле, ускоряя электроны, рассасывает электронное облако и между катодом и анодом появляется ток.
, при достаточно большом расстоянии между электродами, тоже равна нулю. Это происходит оттого, что вылетевшие из катода электроны образуют вблизи него электронное облако. Это приводит к созданию поля, которое тормозит вновь вылетающие электроны. В результате дальнейшая эмиссия электронов прекращается: сколько электронов вылетает из металла, столько же в него возвращается под действием обратного поля электронного облака. Если же между электродами создать внешнее электрическое поле, подсоединив анод А к “+”, а катод К к "-" анодной батареи Ба, то это внешнее электрическое поле, ускоряя электроны, рассасывает электронное облако и между катодом и анодом появляется ток.
Зависимость силы тока 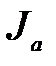 диода от разности потенциалов
диода от разности потенциалов 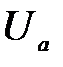 между анодом и катодом выражается законом Богуславского-Ленгмюра:
между анодом и катодом выражается законом Богуславского-Ленгмюра:
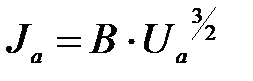 , (5)
, (5)
где В - коэффициент, зависящий от формы и размеров электродов.
Формула (5) выражает уравнение кривой 0123 рис.2в. Для теоретического вывода закона Богуславского-Ленгмюра предположим, что выполняются следующие упрощающие положения:
а) начальная скорость электронов, покидающих катод, равна нулю;
б) пространственный заряд создаёт такое распределение потенциала между электродами, что непосредственно у поверхности катода градиент
потенциала равен нулю: 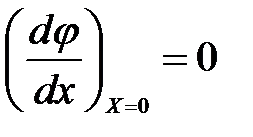 ;
;
в) около катода имеется много электронов и ток далёк от насыщения.
Рассмотрим цилиндрический диод (см. схематический рис.). Обозначим радиус анода - Rа, радиус катода - Rk, длину электродов -  .
.
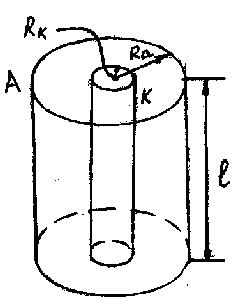
|
| Схематический рисунок к выводу закона Богуславского-Ленгмюра. |
Связь между потенциалом 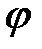 и объёмной плотностью зарядов
и объёмной плотностью зарядов 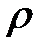 определяется уравнением Пуассона:
определяется уравнением Пуассона:
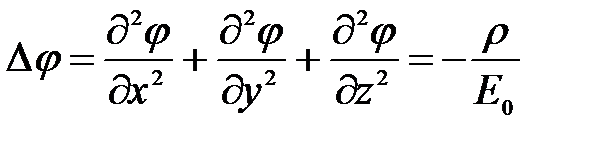 (6)
(6)
В данном случае задачу удобнее решать в цилиндрических координатах:
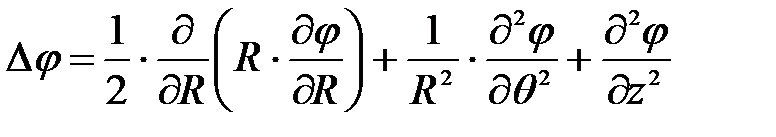 (7) Так как в рассматриваемом случае потенциал является только функцией радиуса R, то последнее выражение (7) упростится и уравнение Пуассона будет иметь вид:
(7) Так как в рассматриваемом случае потенциал является только функцией радиуса R, то последнее выражение (7) упростится и уравнение Пуассона будет иметь вид:
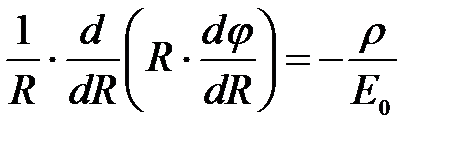 (8)
(8)
Будем искать выражение для электрического тока с единицы длины катода на единицу длины анода:
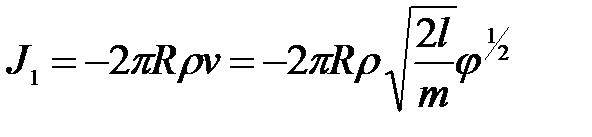 , (9)
, (9)
откуда
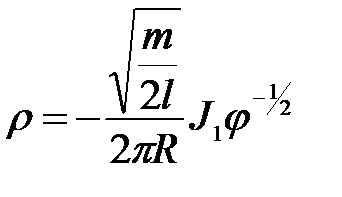 (10)
(10)
Подставляя (10) в (8), получим:
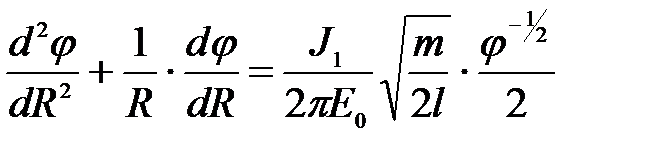 (11)
(11)
При граничных условиях 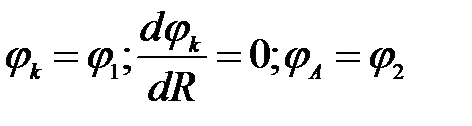 точное решение уравнения (11) имеет вид:
точное решение уравнения (11) имеет вид:
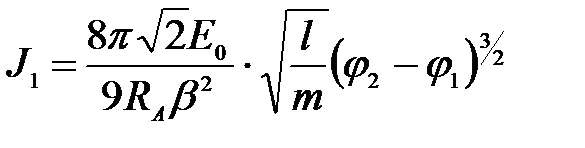 , (12)
, (12)
или
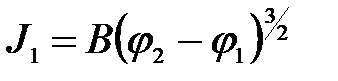 (13)
(13)
Заменяя 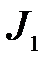 через
через 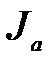 , а
, а 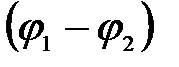 через
через 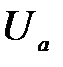 , получим выражение закона Богуславского-Ленгмюра
, получим выражение закона Богуславского-Ленгмюра
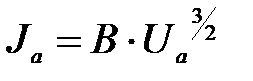 (14)
(14)
В формуле (12) 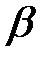 - численный коэффициент, зависящий от отношения Ra/Rk.
- численный коэффициент, зависящий от отношения Ra/Rk.
1.3. Зависимость тока насыщения вакуумного диода от температуры катода
При дальнейшем увеличении разности потенциалов 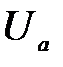 , как это видно из рис.2в, возрастание силы тока
, как это видно из рис.2в, возрастание силы тока 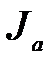 начнёт задерживаться, так как общее число электронов, испускаемых катодом при данной температуре, ограничено. Если
начнёт задерживаться, так как общее число электронов, испускаемых катодом при данной температуре, ограничено. Если 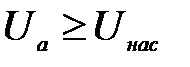 , то все испускаемые при данной температуре катода электроны отсасываются от катода, попадают на анод и дальнейшее возрастание анодного тока прекращается вовсе. При этом достигается ток насыщения
, то все испускаемые при данной температуре катода электроны отсасываются от катода, попадают на анод и дальнейшее возрастание анодного тока прекращается вовсе. При этом достигается ток насыщения 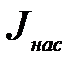 , которому соответствуют горизонтальные части графика 14, 25 и 36 на рис.2в. Из этого рисунка также видно, что при увеличении температуры катода возрастают значения тока насыщения
, которому соответствуют горизонтальные части графика 14, 25 и 36 на рис.2в. Из этого рисунка также видно, что при увеличении температуры катода возрастают значения тока насыщения 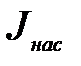 (Т1< Т2< Т3 и, соответственно,
(Т1< Т2< Т3 и, соответственно, 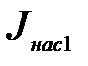 <
< 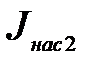 <
< 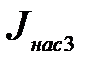 ).
).
На основании сказанного можно считать, что сила тока насыщения 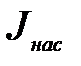 численно равна заряду всех электронов, испускаемых в единицу времени катодом при данной температуре. Следовательно, если мы обозначим через n число электронов, испускаемых катодом в единицу времени, то
численно равна заряду всех электронов, испускаемых в единицу времени катодом при данной температуре. Следовательно, если мы обозначим через n число электронов, испускаемых катодом в единицу времени, то
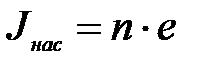 , (15)
, (15)
где 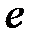 - заряд электрона.
- заряд электрона.
Отсюда
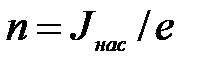 (16)
(16)
| 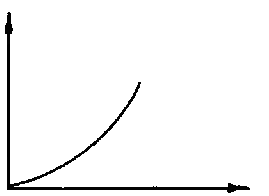
|
| Т | |
| Рис.3. |
Опыты показывают, что сила тока насыщения возрастает чрезвычайно быстро с увеличением температуры катода (характер зависимости 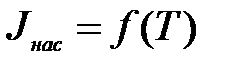 показан на рис.3).
показан на рис.3).
Если вместо тока насыщения 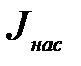 ввести плотность тока насыщения
ввести плотность тока насыщения 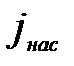 , т.е. величину, представляющую собой ток с единицы поверхности эмитирующего металла, то
, т.е. величину, представляющую собой ток с единицы поверхности эмитирующего металла, то 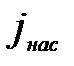 будет измерять число электронов
будет измерять число электронов 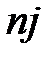 , испускаемых единицей поверхности данного металла при данной температуре Т. Число электронов в металле, способных преодолевать потенциальный барьер на поверхности и выйти в вакуум, быстро увеличивается при повышении температуры. Поэтому и плотность тока насыщения
, испускаемых единицей поверхности данного металла при данной температуре Т. Число электронов в металле, способных преодолевать потенциальный барьер на поверхности и выйти в вакуум, быстро увеличивается при повышении температуры. Поэтому и плотность тока насыщения 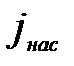 очень сильно зависит от температуры катода. Расчёт на основе квантовой теории показывает, что эта зависимость выражается формулой
очень сильно зависит от температуры катода. Расчёт на основе квантовой теории показывает, что эта зависимость выражается формулой
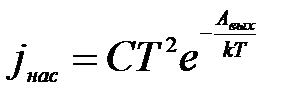 , (17)
, (17)
получившей название формулы Ричардсона-Дэшмана,
где С - постоянная, которая для всех металлов с совершенно чистой поверхностью должна иметь одно и тоже значение;
Т - абсолютная температура катода;
е - основание натурального логарифма;
Авых - величина, имеющая размерность энергии, которая по определению называется термоэлектронной работой выхода данного металла;
к - постоянная Больцмана.
Можно сказать, что работа выхода Авых есть работа, необходимая для перевода электрона с наибольшей кинетической энергией из металла в вакуум без начальной скорости. Формула (17) указывает на чрезвычайно быстрое возрастание плотности тока насыщения 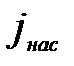 с температурой; в основном закон этого возрастания определяется экспоненциальным множителем
с температурой; в основном закон этого возрастания определяется экспоненциальным множителем 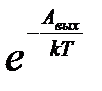 . Теоретическое значение постоянной С для вполне чистой поверхности металла равно 12∙105 А/м2 ∙К2 . На самом деле С варьирует для различных металлов в широких пределах, причём значения С сильно зависят от состояния поверхности металла и в особенности от степени её чистоты. То же имеет место и для работы выхода Авых. Тонкий слой адсорбированных Cs, Ba, Th , окислов бария и т.п. способен весьма сильно снизить работу выхода. Этим обстоятельством пользуются, чтобы получить значительные электронные токи при сравнительно невысоких температурах катода. Так как работа выхода Авых входит в формулу (17) в показатель степени, а величина С является множителем, то для достижения больших токов насыщения основную роль играет работа выхода Авых . Поэтому покрытие поверхности вольфрама Cs, Ba и т.п., как указано, чрезвычайно выгодно, несмотря на малые значения эмиссионной постоянной С. Например, для чистой поверхности вольфрама работа выхода Авых = 4,5 эВ и эмиссионная постоянная С = 6∙105 А/м2 ∙К2 . Тогда плотность тока насыщения
. Теоретическое значение постоянной С для вполне чистой поверхности металла равно 12∙105 А/м2 ∙К2 . На самом деле С варьирует для различных металлов в широких пределах, причём значения С сильно зависят от состояния поверхности металла и в особенности от степени её чистоты. То же имеет место и для работы выхода Авых. Тонкий слой адсорбированных Cs, Ba, Th , окислов бария и т.п. способен весьма сильно снизить работу выхода. Этим обстоятельством пользуются, чтобы получить значительные электронные токи при сравнительно невысоких температурах катода. Так как работа выхода Авых входит в формулу (17) в показатель степени, а величина С является множителем, то для достижения больших токов насыщения основную роль играет работа выхода Авых . Поэтому покрытие поверхности вольфрама Cs, Ba и т.п., как указано, чрезвычайно выгодно, несмотря на малые значения эмиссионной постоянной С. Например, для чистой поверхности вольфрама работа выхода Авых = 4,5 эВ и эмиссионная постоянная С = 6∙105 А/м2 ∙К2 . Тогда плотность тока насыщения 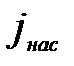 по формуле (17) при температуре Т=
по формуле (17) при температуре Т=
1000 К будет:
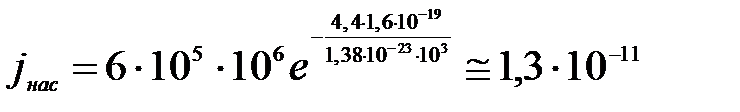 А/м2
А/м2
Та же поверхность вольфрама при Т=3000 К даёт 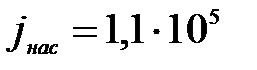 А/м2, т.е. повышение температуры катода в 3 раза ведёт к возрастанию тока насыщения почти в 1016 раз. Для поверхности вольфрама, покрытого цезием, имеем Авых= 1,36 эВ и С = 0,32∙105 А/м2.К2, тогда из формулы (17) для этого случая при температуре катода Т=1000 К получается плотность тока насыщения
А/м2, т.е. повышение температуры катода в 3 раза ведёт к возрастанию тока насыщения почти в 1016 раз. Для поверхности вольфрама, покрытого цезием, имеем Авых= 1,36 эВ и С = 0,32∙105 А/м2.К2, тогда из формулы (17) для этого случая при температуре катода Т=1000 К получается плотность тока насыщения 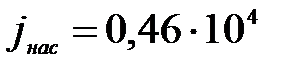 А/м2. Таким образом, покрытие поверхности вольфрама цезием позволяет получать при температуре накала катода Т=1000 К токи насыщения примерно в 3∙1014 раз больше, чем в случае чистого вольфрама при той же температуре.
А/м2. Таким образом, покрытие поверхности вольфрама цезием позволяет получать при температуре накала катода Т=1000 К токи насыщения примерно в 3∙1014 раз больше, чем в случае чистого вольфрама при той же температуре.
Измерение тока насыщения 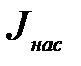 позволяет найти работу выхода Авых. В самом деле, логарифмируя формулу (17), получим:
позволяет найти работу выхода Авых. В самом деле, логарифмируя формулу (17), получим:
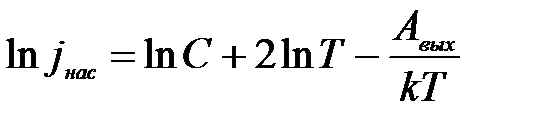 (18)
(18)
Примечание: При логарифмировании здесь и далее следует иметь в виду, что для именованных (имеющих размерность) чисел этот математический приём не имеет смысла, поэтому предполагается, что мы логарифмируем лишь отвлечённое число или алгебраическое выражение, состоящее из отвлечённых чисел.
Сумму первых двух членов 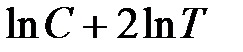 можно считать приблизительно постоянной, так как при изменении температуры значение
можно считать приблизительно постоянной, так как при изменении температуры значение 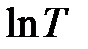 меняется гораздо медленнее, чем 1/Т. Поэтому приближённо имеем:
меняется гораздо медленнее, чем 1/Т. Поэтому приближённо имеем:
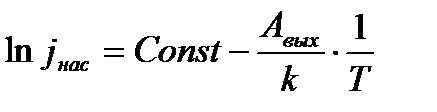 (19)
(19)
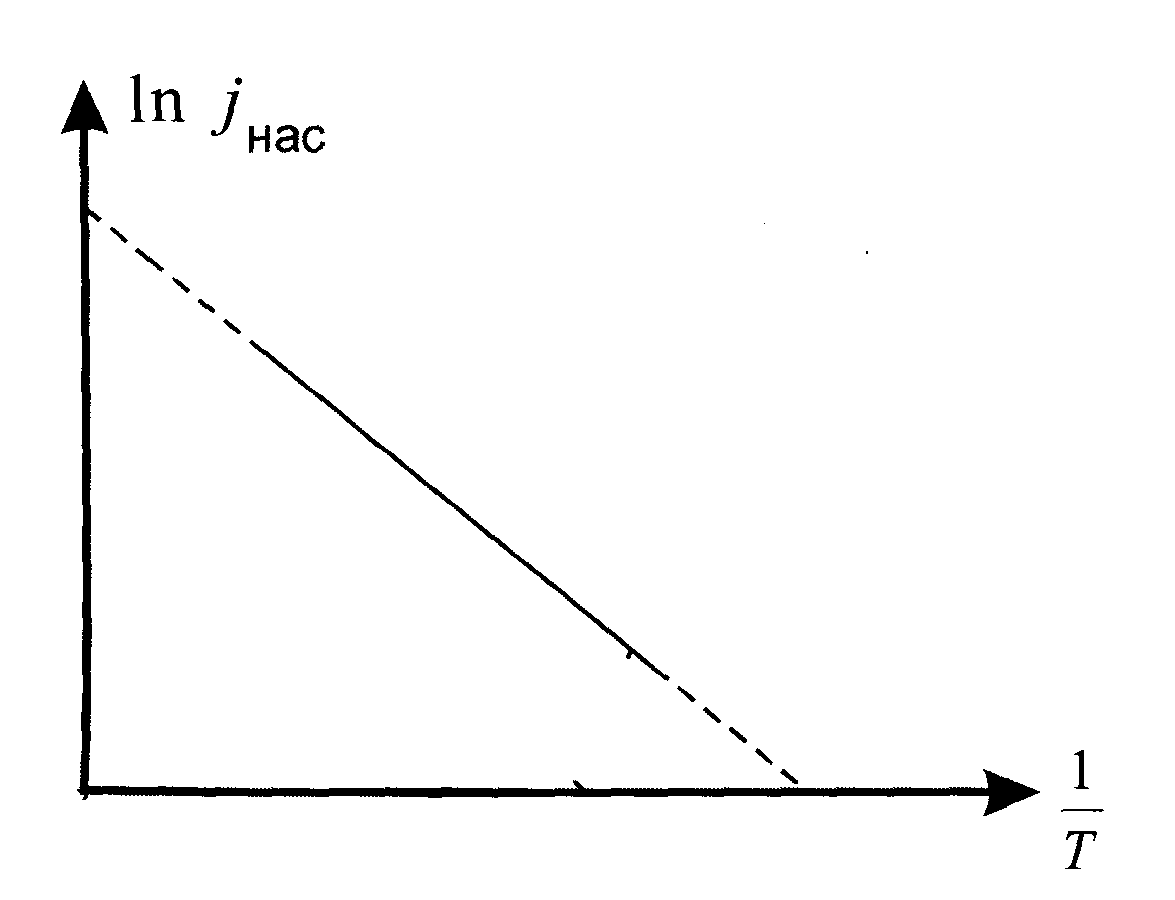
Если по оси ординат Y отложить 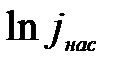 , а по оси абсцисс Х 1/Т (рис.4), то зависимость
, а по оси абсцисс Х 1/Т (рис.4), то зависимость 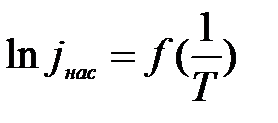 по формуле (19) выразится прямой. Такой характер зависимости
по формуле (19) выразится прямой. Такой характер зависимости 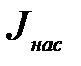 от Т хорошо подтверждается опытом. Из графика видно, что величина Авых / к может бытьнайдена из соотношения величин катетов треугольника, гипотенузой которого является прямая (или её часть):
от Т хорошо подтверждается опытом. Из графика видно, что величина Авых / к может бытьнайдена из соотношения величин катетов треугольника, гипотенузой которого является прямая (или её часть):
Авых / к = ln jнас / Т-1. (20)
Таким образом, получив по экспериментальным данным зависимость 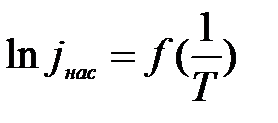 , мы можем найти по формуле (20) значение работы выхода Авых= кТ ln jнас.
, мы можем найти по формуле (20) значение работы выхода Авых= кТ ln jнас.
1.4. Вакуумная электронная лампа (диод) как выпрямитель
Так как раскалённый катод электронной лампы испускает только электроны, но не положительные ионы, лампа пропускает ток только тогда, когда её катод соединён с отрицательным полюсом источника. При перемене полярности приложенного напряжения все термоэлектроны возвращаются в катод и ток через лампу не проходит. Поэтому лампа обладает односторонней проводимостью, или вентильным свойством.
|
| Рис. 4. |
Вентильное действие диода широко используют для устройства выпрямителей, предназначенных для превращения переменного тока в постоянный. Простейшая схема выпрямителя с диодом показана на рис.5. Переменное напряжение между точками Б и В (входное напряжение ~Uвх) изменяется во времени согласно кривой а). Вследствие вентильного свойства лампы ток в нагрузочном сопротивлении R имеется только в те полупериоды, когда на катод подается “ - ” и лампа пропускает ток. Поэтому выходное напряжение U вых на сопротивлении R изображается кривой б) и мы получаем пульсирующее напряжение одного знака.
На рис.6 показана схема двухполупериодного выпрямителя. В каждый момент времени работает лишь одна из ламп, а именно та, напряжение на которой соответствует пропускному направлению.
Дата добавления: 2015-02-16; просмотров: 2765;
