Винтовые линии

Из пространственных кривых линий наибольшее применение в технике нашли винтовые линии. Используются винтовые линии как базовые при образовании винтовых поверхностей, которые применяются в резьбовых соединениях (болты, винты, шпильки, гайки), в механизмах для преобразования вращательного движения в поступательное (ходовые винты), в транспортирующих устройствах (винтовые спуски), в качестве рабочих органов специальных конвейеров и штабелей (шнеки), в червячных передачах и других устройствах.

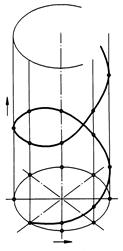
A4 A1 A2 A3 A5 i L A Рис. 127

Винтовая линия L (рис. 127) образуется точкой A, непрерывно вращающейся вокруг неподвижной оси i и одновременно поступательно перемещающейся параллельно этой же оси.

На рис. 128 приведен комплексный чертеж цилиндрической винтовой линии равного уклона l, ось вращения i которой занимает положение горизонтально - проецирующей прямой. Горизонтальная проекция этой линии l₁ представляет собой окружность радиуса r, а фронтальная l₂ - синусоиду.

Величину перемещения точки в направлении оси, соответствующую одному полному обороту этой точки вокруг оси, называют шагом винтовой линии и обозначают S.

Величину перемещения точки в направлении оси при повороте ее вокруг оси на угол, равный одному радиану, называют единичным шагом гелисы и обозначают

.

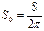На ортогональном чертеже гелиса обычно задается диаметром, шагом и направлением (ходом). Гелиса имеет правый ход, если стрелка направления вращения точки на горизонтальной проекции совпадает с направлением хода часовой стрелки и точка опускается по траектории к плоскости проекций перпендикулярной оси. Если стрелка указывает направление обратное ходу часовой стрелки, то цилиндрическая винтовая линия имеет левый ход.

При построении винтовой линии (см. рис. 128), когда заданы радиус r и шаг S, необходимо разделить окружность на равное число частей и шаг S горизонтальными линиями на такое же число частей. Точка пересечения линий связи, проведенных из горизонтальных проекций точек 1₁, 2₁, 3₁ … соответствующими горизонтальными линиями на фронтальной плоскости проекций, определяют положение точек винтовой линии 1₂, 2₂, 3₂ … Соединив их плавной кривой линией, получим фронтальную проекцию цилиндрической винтовой линии равного уклона.

Разверткой такой линии является прямая линия, угол наклона которой к горизонтальной линии ( называется углом подъема винтовой линии (уклона).

Цилиндрическая винтовая линия постоянного уклона так же, как и прямая линия и окружность, обладает свойством сдвигаемости. Это свойство заключается в том, что любой отрезок линии можно сдвигать вдоль самой линии. При этом все точки отрезка будут совпадать с точками линии.

В качестве задающей поверхности при образовании винтовой линии можно использовать любую поверхность вращения. Так, коническая винтовая линия получится, если в качестве задающего будет принят прямой круговой конус.

Контрольные вопросы

1. Какие кривые линии называют алгебраическими и какие трансцендентными?

2. Что называют порядком алгебраической кривой?

3. Что называют кривизной плоской кривой и как ее определяют графически?

4. Дайте определение эволюты и эвольвенты плоской кривой.

5. Назовите основные свойства эволют и эвольвент.

6. Какие кривые линии называют монотонными?

7. Какие кривые линии называют овалами? Покажите примеры овалов.

8. Какие кривые линии называют соприкасающимися?

9. Какое преобразование плоских кривых называют коихоидальным, инверсией, конформным?

10. Какие кривые линии называют кривыми линиями второго порядка? Расскажите о каждой из них.

11. Какие кривые называют эквидистантными?

12. Какие пространственные кривые называют гелисами и как их задают на эпюре Монжа?

13. Как определяют на чертеже направление (ход) цилиндрической винтовой линии?

14. Расскажите о конических винтовых линиях.