Проекционные свойства кривых линий

Как указывалось выше, в начертательной геометрии изучение кривых и решение разнообразных задач осуществляется по их проекциям на комплексном чертеже. Ортогональные проекции кривых линий обладают рядом проекционных свойств, основными из которых являются следующие:

1. Ортогональной проекцией кривой линии являются множество однозначных ортогональных проекций точек этой линии.

2. Если точка принадлежит кривой линии, то ее проекции принадлежат одноименным проекциям этой линии.

3. В общем случае проекцией кривой линии является плоская кривая линия. Как исключение, плоская кривая линия может проецироваться на плоскость проекций, перпендикулярную плоскости, в которой расположена кривая, в прямую линию.

4. Кривая линия не определяется однозначно своими проекциями, если хотя бы одна из ее проекций дважды пересекает линию связи, проведенную через какую-либо точку кривой (рис. 122 и 123). В этом случае необходимы дополнительные условия, в качестве которых могут быть использованы проекции точки, лежащей на кривой.

5. Обыкновенные и особые точки кривых линий проецируются в точки того же вида, за исключением случая, когда вырождаются в прямую линию.

6.

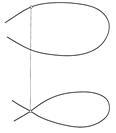
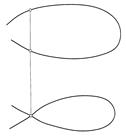
Рис. 122 Рис. 123

7. Проекции касательной и нормали в общем случае не перпендикулярны, если только положение касательной и нормали в пространстве не подчиняется условиям теоремы о проецировании прямого угла.

8. Если две кривые линии пересекаются, то точка пересечения одноименных проекций лежит на одной линии связи.

9. Порядок проекций алгебраической кривой равен порядку самой линии или, в частном случае, когда кривая расположена в плоскости, перпендикулярной плоскости проекций, порядок проекций будет меньше.

10. Ортогональная проекция кривой второго порядка в общем виде является кривой второго порядка того же вида. Например, гипербола проецируется в гиперболу, эллипс – в эллипс или окружность (как частный случай) и т.д.