Плоские кривые линии. Касательная, нормаль, кривизна
Плоская кривая линия (a) построена в плоскости S (рис. 106).
Касательной к плоской кривой линии в некоторой точке называют предельное положение секущей, когда две общие точки пересечения, стремясь друг к другу, совпадают. В общем случае касательная может занять разное положение в зависимости от того, в какую сторону поворачивается секущая относительно некоторой неподвижной точки кривой. Поэтому для характеристики точек плоской линии принято использовать полукасательные.
На рис. 106 показано образование полукасательной t1, когда точка A на секущем луче [MA] перемещает-
ся к неподвижной точке M. Предельное положение
Рис. 106 секущей называют полукасательной t1.
Аналогично получают другую полукасательную t2 при перемещении точки B второго секущего луча [MB] к точке M.
Кривая линия в точке M имеет две разнонаправленные полукасательные. Если в точке M разнонаправленные полукасательные к кривой (a) продолжают одна другую и определяют одну прямую линию – касательную, кривая линия в точке M называется плавной. Кривая, плавная во всех ее точках, называется плавной кривой линией.
Нормалью (n) плоской кривой в данной точке M называется перпендикуляр к полукасательной (t), лежащей в плоскости кривой и направленной внутрь ее.
Поскольку в каждой точке кривой можно построить две полукасательные, то и нормалей также будет две, которые в некоторых случаях могут совпадать (см. рис. 106).
При параллельном проецировании порядок плоской алгебраической кривой не изменяется.
Движение точки вдоль кривой (a) связано с непрерывным изменением двух величин: расстояния S, на которое удалена точка от начального своего положения, и угла a поворота касательной относительно начального положения. Если с увеличением пути S движения точки непрерывно увеличивается и угол a, кривая линия называется простой.
 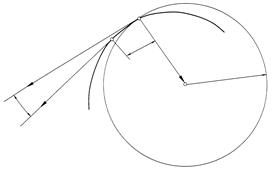 Рис. 107
Рис. 107
|
Угол a между касательными в двух бесконечно близких точках кривой, отнесенный к длине дуги между этими точками, определяют кривизну кривой. Кривизна K – предел отношения угла Da между двумя соседними касательными к соответствующей дуге DS (рис. 107), т.е.
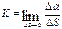
Графически кривизна численно равна величине, обратной радиусу rk окружности кривизны – окружности соприкасающейся кривой в данной точке и имеющей с ней общие полукасательную и нормаль:
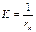
Центр окружности кривизны Ok называют центром кривизны. Он всегда располагается на нормали.
Кривизна прямой в любой ее точке равна 0. Кривизна произвольной кривой в разных точках различна.
Умение графически определять полукасательную, нормаль, радиус и центр кривизны весьма важно при построении плоских кривых с определенными заданными параметрами.
Поскольку касательная и нормаль являются взаимно перпендикулярными прямыми, то положение одной из них однозначно определяют положение другой.
Построение касательной и нормали в общем случае осуществляется приближенно при помощи кривой ошибок. В зависимости от постановки задачи возможны различные способы построения этих параметров.
Для построения касательной t к кривой l, проходящей через точку А, расположенной вне кривой (рис. 108), необходимо через нее провести пучок секущих прямых a1, a2, a3 и т.д. Через середины хорд проводится кривая m, называемая кривой ошибок.
Искомая касательная t проходит через точку M пересечения кривой ошибок с заданной кривой. Нормаль n располагается перпендикулярно касательной.
Если необходимо провести касательную к кривой параллельно некоторому направлению S, то построения выполняют аналогично рассмотренному случаю, только семейство секущих проводят параллельно заданному направлению (рис. 109).



При построении касательной в заданной точке M кривой первоначально проводят произвольную прямую b примерно перпендикулярно искомой касательной (рис. 110).
Затем через точку M проводят семейство секущих a1, a2, a3, a4, на которых откладывают от прямой b отрезки, равные соответствующим хордам. При этом необходимо их располагать относительно прямой b так же, как расположены хорды относительно точки M. Полученные точки определяют кривую ошибок m, точка K пересечения которой с прямой b задает направление касательной t.
Если требуется провести нормаль к кривой из точки A, лежащей вне кривой, необходимо построить семейство концентрических окружностей с центром в точке A и пересекающих заданную кривую l (рис. 111).
  Рис. 111
Рис. 111
|
По точкам пересечения окружностей с кривой строят хорды, из концов которых проводят разнонаправленные перпендикуляры к ним. На перпендикулярах откладываются отрезки, равные длине соответствующих хорд. Через концы этих отрезков проводят кривую ошибок m, которая пересекает заданную кривую линию в точке M, через которую проходит нормаль n и касательная t.
Центр и радиус кривизны кривой в заданной точке M строят, используя касательную и нормаль. Для этого через ряд точек кривой A, B, C вблизи точки M и саму точку M проводят касательные tА, tВ, tС и tМ (рис. 112).
Через точки A1, B1, C1, M1, расположенные на одинаковом расстоянии от соответствующих точек кривой A, B, C, M, проводят плавную кривую линию m. В точках M и M1 строят нормали к кривым l и m, точка пересечения которых Ok определяет центр кривизны кривой l в точке M.
Радиус кривизны 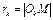 .
.

Рис. 112
Дата добавления: 2015-02-25; просмотров: 2442;

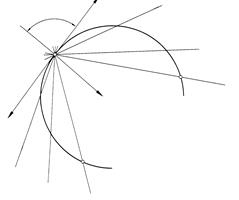

 Рис. 107
Рис. 107
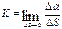
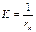




 Рис. 111
Рис. 111
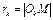 .
.
