Пересечение многогранника прямой линией

Точки пересечения прямой линии с гранями любого многогранника определяем по общей схеме:

1. Заключаем прямую линию во вспомогательную плоскость частного положения;

2. Строим линию пересечения (сечение) многогранника вспомогательной плоскостью;

3. Находим искомые точки пересечения прямой с многогранником, как точки пересечения прямой с построенным выше сечением.

На рис. 100 показано построение точек пересечения M и N прямой ℓ с трехгранной пирамидой SАВC. Используем схему решения задач на пересечение прямой линии с многогранником:

1. Заключаем прямую ℓ (ℓ₁, ℓ₂) во фронтально проецирующую плоскость S (S₂);

2. Строим линию пересечения (сечения)

многогранника плоскостью S :

123 (1₁2₁3₁, 1₂2₂3₂);

3. Определяем точки пересечения

М(М₁М₂)и N(N₁N₂) прямой ℓ (ℓ₁, ℓ₂) с

построенным сечением 123 (1₁2₁3₁,

1₂2₂3₂);

М₁= ℓ₁ Ⴖ 1₁3₁; N₁= ℓ₁ Ⴖ 2₁3₁;

М₂ Î ℓ₂; N₂ Î ℓ₂.

4. Определяем видимость прямой относительно

многогранника. Так как точки М и N ле-

жат на видимых гранях пирамиды, то часть

прямой линии ℓ до этих точек будет видимой

как на плоскости П₁, так и на плоскости П₂.

Часть прямой линии ℓ (между точками М

Рис. 100 и N ), находящаяся внутри многогранника,

всегда не видна.

Контрольные задания по теме «Многогранники»

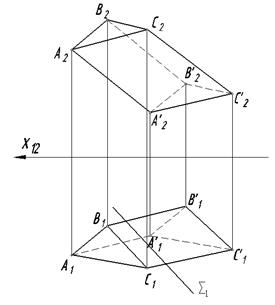
1. Построить проекции сечения призмы плоскостью частного положения S.

2. Построить проекции сечения пирамиды плоскостью общего положения Q.

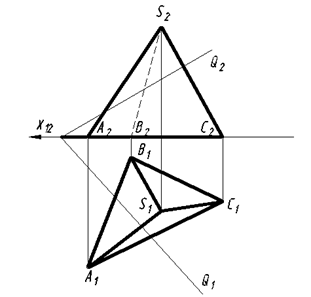
Рис. 102

Пример 1. Найти недостающие проекции точек М и N, принадлежащих граням многогранни-

ка, (рис. 103).

Дано: М₂ и N₁. Точка М Î AA¢DD¢, a N Î CC¢DD¢ .

Чтобы построить горизонтальную проекцию М₁ , на плоскости П₂ через М₂ строим прямую D1(D₂1₂), затем строим D₁1₁. М₁ Î D₁1₁.

Чтобы построить фронтальную проекцию N₂ , на плоскости П₁ через N₁ строим прямую D¢2(D¢₁2₁), затем строим D¢₂2₂. N₂ Î D¢₂2₂.

Рис. 103

Пример 2. Построить сечение пирамиды SАВC плоскостью общего положения S (h, f ), рис. 104.

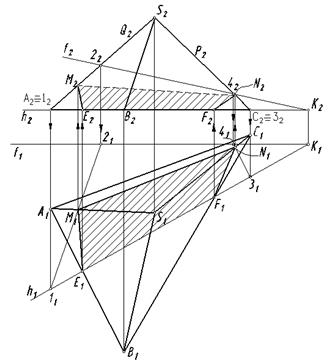
Рис. 104

Основание пирамиды SАВC ∆ АВС ‖ П₁ ; h ‖ П₁ . Основание пирамиды АВС и горизонталь пересекаются на П₁ в точках E и F. E₁F₁ =А₁В₁С₁ Ⴖ h₁; E₂F₂ Î А₂В₂С₂.

Нахождение других точек сечения сводится к решению задачи на пересечение прямой (ребра пирамиды) с заданной плоскостью. Заключаем ребро SА во фронтально проецирующую плоскость Q (Q₂). Строим линию пересечения 12 (1₁2₁, 1₂2₂) плоскости S (h, f ) и вспомогательной плоскости Q.

· 1Î h, 1₁Î h₁, 1₂Î h₂; 2Î f , 2₁Î f₁, 2₂Î f₂.

· М₁ = 1₁2₁ Ⴖ S₁А₁, М₂ Î S₂А₂ .

Аналогичные построения выполняем для определения точки N : N = SC Ⴖ S (h, f).

Стрелки на линиях связей показывают последовательность решения. Найденные точки E,F,N,M, соединяем как на П₁, так и на П₂ в замкнутый контур с учетом видимости граней пирамиды. Это будет искомое сечение пирамиды SАВC заданнойплоскостью общего положения S (h, f ).

Контрольные вопросы

1. Что называется многогранником?

2. Какие многогранники называются выпуклыми?

3. Что называется правильными многогранниками?

4. Что называется числом Эйлера многогранника?

5. Как решаются задача на построение сечения многогранника проецирующей плоскостью?

6. Схема решения задачи на пересечение многогранника прямой линией?

7. Как решается задача на построение сечения многогранника плоскостью общего положения?