Пространственные кривые линии
Пространственной или линией двоякой кривизны принято называть кривую, все точки которой не принадлежат одной и той же плоскости. Пространственные кривые линии в начертательной геометрии обычно рассматриваются как результат пересечения поверхностей.
Поскольку пространственные линии занимают более сложное положение в пространстве, чем плоские, проводится анализ общих свойств по комплексному чертежу и локальных свойств в окрестностях какой-либо ее точки по проекциям на гранях так называемого сопровождающего трехгранника (трехгранник Френе). Сопровождающий трехгранник жестко связан с движущейся по кривой точкой и, следовательно, для каждой точки кривой будет занимать разные, характерные для этой точки положения.
На рис. 124 изображена пространственная кривая l и на ней точка M. Проведем через эту точку две секущие прямые a и b, которые пересекут кривую в точках A и B.
 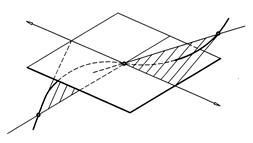
|
При перемещении точек A и B к точке M секущие будут поворачиваться и, когда эти точки совпадут, займут положение полукасательных t1 и t2. Если точка M обыкновенная, то полукасательные имеют противоположное направление, образуя общую касательную. Через касательную к кривой в данной точке M можно провести бесконечное множество плоскостей. Одна из них называется соприкасающейся плоскостью Г. Положение этой плоскости можно представить себе следующим образом. Каждая секущая и соответствующая ей полукасательная образуют плоскости (aLt1) и (bLt2). При приближении точек A и B к точке M эти плоскости будут поворачиваться и в пределе, когда точки A и B совпадут с M, займут положение соприкасающейся плоскости Г.
Рис 124 Через точку M можно провести бесконечное множест-
во прямых, перпендикулярных касательной. Все они будут лежать в плоскости Ф (рис. 125), которая называется нормальной плоскостью.
Одна из этих нормалей принадлежит соприкасающейся плоскости Г и называется главной нормалью nГ. Другая нормаль, перпендикулярная к соприкасающейся плоскости, называется бинормалью nр. Бинормаль и касательная определяют плоскость Р, которая называется спрямляющей плоскостью (рис. 126).


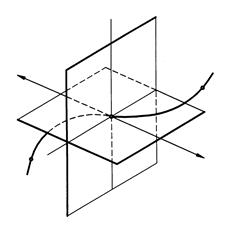
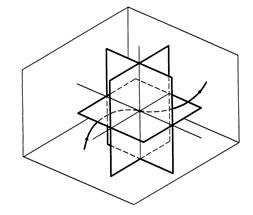
Рис. 125 Рис. 126
Соприкасающаяся Г, нормальная Ф и спрямляющая Р плоскости образуют сопровождающий трехгранник. Локальные свойства кривой в окрестностях точки M исследуют по проекциям линии на плоскостях сопровождающего трехгранника или, что равноценно, с помощью проекций на плоскостях проекций П1, П2 и П3, выбрав их положение параллельно плоскостям Г, Ф и Р (рис. 126).
Проекционные свойства пространственных кривых линий во многом аналогичны свойствам плоских кривых. Однако имеются и исключения. Так, например, пространственная кривая линия проецируется только в плоскую кривую, вид точек на проекциях кривых линий может не соответствовать виду самих точек.
Дата добавления: 2015-02-25; просмотров: 1423;
