Многопериодная модель потребления

Рассмотрим многопериодную модель. Будем считать, что налоги и трансферты отсутствуют и в результате доход совпадает с располагаемым доходом. Пусть доход потребителя (доход, не связанный с активами) в периоде t равен Y_t. Будем считать, что потребитель имеет (до начала первого периода) первоначальные активы B₀ (наследство). Пусть потребитель может свободно занимать и давать взаймы по одинаковой номинальной ставке процента 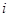, причем (ожидаемая) реальная ставка процента одинакова для всех периодов. В дальнейшем будем считать, что ожидания агентов относительно реальной ставки процента совпадают с фактической ставкой 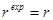. Это предположение означает, что у населения есть основания полагать, что ожидаемая инфляция будет неизменной для рассматриваемого временного горизонта. Кроме того, будем считать, что налоги и трансферты отсутствуют. Тогда активы периода t будут равны активам предыдущего периода с поправкой на процент по этим активам плюс доход периода t за вычетом потребления в этом периоде:

(1) .

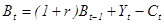Напомним, что под сбережениями индивидуума мы понимаем ту часть совокупного дохода, которая не потребляется. Совокупный доход периода t в нашем примере состоит из дохода, не связанного с активами, Y_t, и процентам по активам предыдущего периода rB_t-1. Таким образом, сбережения периода t равны

.

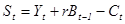Подставляя (2) в (1) после преобразований получаем, что изменение активов, в свою очередь, равно сбережениям: 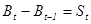, которые могут быть положительны (в этом случае потребитель действительно сберегает) и отрицательны (в этом случае потребитель является заемщиком).

Многопериодное бюджетное ограничение.

Рассмотрим двухпериодную модель и предположим для простоты, что потребитель не обладает никакими первоначальными активами (то есть В₀=0) и не планирует оставлять наследство в конце жизни (В₂=0). Тогда сбережения первого периода составят:

(3) ,

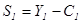а сбережения второго периода равны:

(4) .

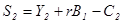Поскольку первоначальные активы отсутствуют, то 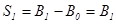. Учитывая, что, по предположению, активы в конце жизни равны нулю, то сбережения второго периода равны: 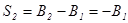, то есть во втором периоде полностью проедаются сбережения первого периода. Из соотношений (3) и (4) с учетом того, что 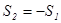, получаем двухпериодное бюджетное ограничение:

(5) C₁(1+r)+C₂=Y₁(1+r)+Y₂

В рассматриваемой модели потребление в разные периоды времени играет роль разных товаров, и мы имеем стандартное бюджетное ограничение, где в левой части стоят расходы, а в правой – доходы потребителя:

Бюджетное ограничение, записанное таким образом, называют ограничением, приведенном к будущему (второму) периоду, поскольку сегодняшние величины доходов и расходов записываются с поправкой на процент, который они могут принести в следующем периоде. Поделив левую и правую часть ограничения (5) на (1+r), мы получим бюджетное ограничение в терминах стоимости, приведенной к начальному моменту времени.

Заметим, что, если бы потребитель имел (до начала первого периода) первоначальные активы B₀ и собирался в конце второго периода оставить наследство своим потомкам, равное величине B₂, то бюджетное ограничение приняло бы следующий вид:

(6) C₁(1+r)+C₂= B₀(1+r)²+Y₁(1+r)+Y₂ -B₂

Описав бюджетное ограничение, перейдем к предпочтениям потребителя. Будем считать, что предпочтения потребителя описываются функцией полезности, зависящей от потребления в настоящем и в будущем периодах: u(C₁, C₂).

Итак, потребитель решает стандартную задачу максимизации полезности при бюджетном ограничении:

max u(C₁, C₂)

C₁(1+r)+C₂=Y₁(1+ r)+Y₂

Решение этой задачи несложно изобразить графически (смотри Рис.1).

Рис 1. Графическое представление двухпериодной модели потребления

От каких же параметров зависит текущее потребление, то есть оптимальное потребление первого периода? В первую очередь оптимальное потребление зависит от доходов, причем, как мы видим, текущее потребление зависит не только от текущего дохода Y₁ , но и от будущего дохода Y₂. Если мы будем считать потребление в каждом периоде нормальным товаром (что представляется разумным в сильно агрегированной экономике), то рост доходов будет способствовать и росту потребления.

Другим фактором, влияющим на текущее потребление, является наклон бюджетной линии, определяемый ставкой процента. Как же изменится потребление с изменением процентной ставки? Следует отметить, что процентная ставка в рассматриваемой модели играет роль цены и ее изменение влечет соответственно два эффекта: эффект замещения и эффект дохода. Если ставка процента растет, то сегодняшнее потребление становится дороже, что вынуждает потребителя сокращать текущее потребление С₁ и увеличивать будущее потребление С₂. С эффектом дохода все не так однозначно, как с эффектом замещения, поскольку знак эффекта дохода зависит от типа потребителя:

Если мы имеем дело с чистым заемщиком, то есть с потребителем, который в первом периоде потребляет больше своего дохода (С₁^*>Y₁), то он проигрывает от повышения процентной ставки, так как увеличиваются проценты выплаты по кредиту, который он взял в первом периоде и, следовательно, его доходы уменьшаются, что и ведет к сокращению текущего потребления.

В случае с чистым кредитором (то есть, с потребителем, который в первый период потребляет не весь свой доход, а остаток сберегает) ситуация выглядит иначе. Он выигрывает от повышения процентной ставки, так как ему возвращают долг с более высокими процентами, в результате его доходы возрастают, и увеличивается текущее потребление.

Рассмотренные выше рассуждения можно получить формально из уравнения Слуцкого для случая натурального дохода:

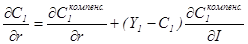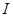, где -доход в виде денег.

Первое слагаемое в правой части отражает эффект замещения и является отрицательным, а второе слагаемое соответствует эффекту дохода и, как, следует из уравнения знак этого слагаемого зависит от соотношения между текущим потреблением и доходом, то есть, от того является ли потребитель заемщиком или же кредитором.

Итак, мы можем заключить, что для заемщика рост ставки процента отрицательно влияет на текущее потребление, поскольку эффект замещения и эффект дохода действуют в одном направлении. В случае чистого кредитора влияние ставки процента на потребление в первом периоде неоднозначно: потребление падает, если доминирует эффект замещения, и растет, если доминирует эффект дохода. Что же можно заключить о влиянии ставки процента на совокупное потребление? Если предположить, что в процессе агрегирования эффекты дохода для кредиторов и заемщиков уничтожаются, то останутся лишь эффекты замещения, которые ведут к падению текущего потребления в результате роста процентной ставки.