Теория перманентного (или постоянного) дохода

Согласно этой теории потребление определяется не текущим, а неким усредненным доходом, который М.Фридман назвал перманентным доходом. В соответствии с современным представлением теории перманентного дохода можно дать следующее определение концепции перманентного дохода в рамках многопериодной модели потребления. Перманентным доходом для данного фактического потока доходов Y₁, Y₂, . . . ,Y_T называется постоянный доход YP, приведенная величина которого равна приведенной величине фактического потока доходов Y₁, Y₂, . . . ,Y_T:

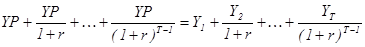
В частности, для двухпериодной модели мы получаем, что перманентный доход равен: .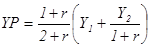

Итак, вернемся к задаче максимизации полезности для репрезентативного потребителя. Рассмотрим аддитивно сепарабельную функцию полезности:

(7)

Максимизируя (7) при многопериодном бюджетном ограничении:

(8) ,

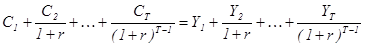получаем,

(9) .

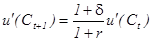Если ставка процента равна норме межвременных предпочтений (r=d), то предельные полезности в разные периоды времени должны быть равны: 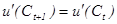, откуда в силу строгой вогнутости u( ) следует равенство потребления в разные периоды времени: 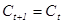, то есть потребитель выбирает сглаженное потребление. Принимая во внимание бюджетное ограничение и определение перманентного дохода, получаем:

.

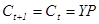Потребление в условиях неопределенности.

Однако рассмотренная выше модель игнорирует проблему неопределенности. Мы не знаем в точности, каковы наши будущие доходы, в связи с этим имеет смысл обратиться к задаче максимизации ожидаемой полезности, предполагая, что потребитель имеет рациональные ожидания. Гипотеза рациональных ожиданий означает, что потребитель базирует свои представления о будущем на определенной модели поведения (в нашем случае модели многопериодного выбора), принимая во внимание всю имеющуюся на данный момент информацию. Таким образом, перманентный доход может быть изменен только, если поступит какая-то новая информация, неизвестная ранее.

Для задачи максимизации ожидаемой полезности соотношение (9) при условии, что r=d примет вид:

(10) ,

где E- математическое ожидание. Рассмотрим квадратичную функцию полезности 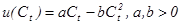. Тогда из условия (10) получаем:

(11) .

Полученное соотношение говорит, что будущее потребление будет совпадать с сегодняшним, если не происходит ничего неожиданного. Иначе говоря, будущее потребление можно представить в следующем виде:

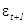(12) , где -случайная ошибка с математическим ожиданием, равным нулю, которая отражает новую информацию.