Червячные передачи.
Червячные передачи (рис.5.53) относятся к передачам с перекрещивающимися осями валов. Угол перекрещивания обычно равен 90°. Другие углы применяются редко.
Движение в червячной передаче образуется по принципу винтовой пары.
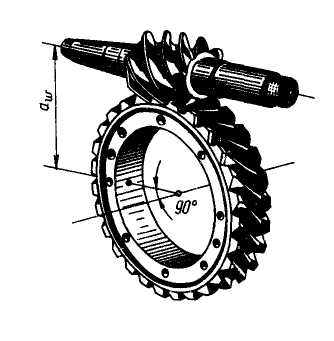
Рис. 5.53
Червячная пара
Здесь, как и в предыдущих передачах, различают диаметры начальных цилиндров (dw1- червяка, dw2- червячного колеса), делительных цилиндров (d1- червяка, d2- червячного колеса); межосевое расстояние Aw. В передачах без смещения dw1= d1; dw2= d2 . Точка касаниия начальных цилиндров является полюсом зацепления.
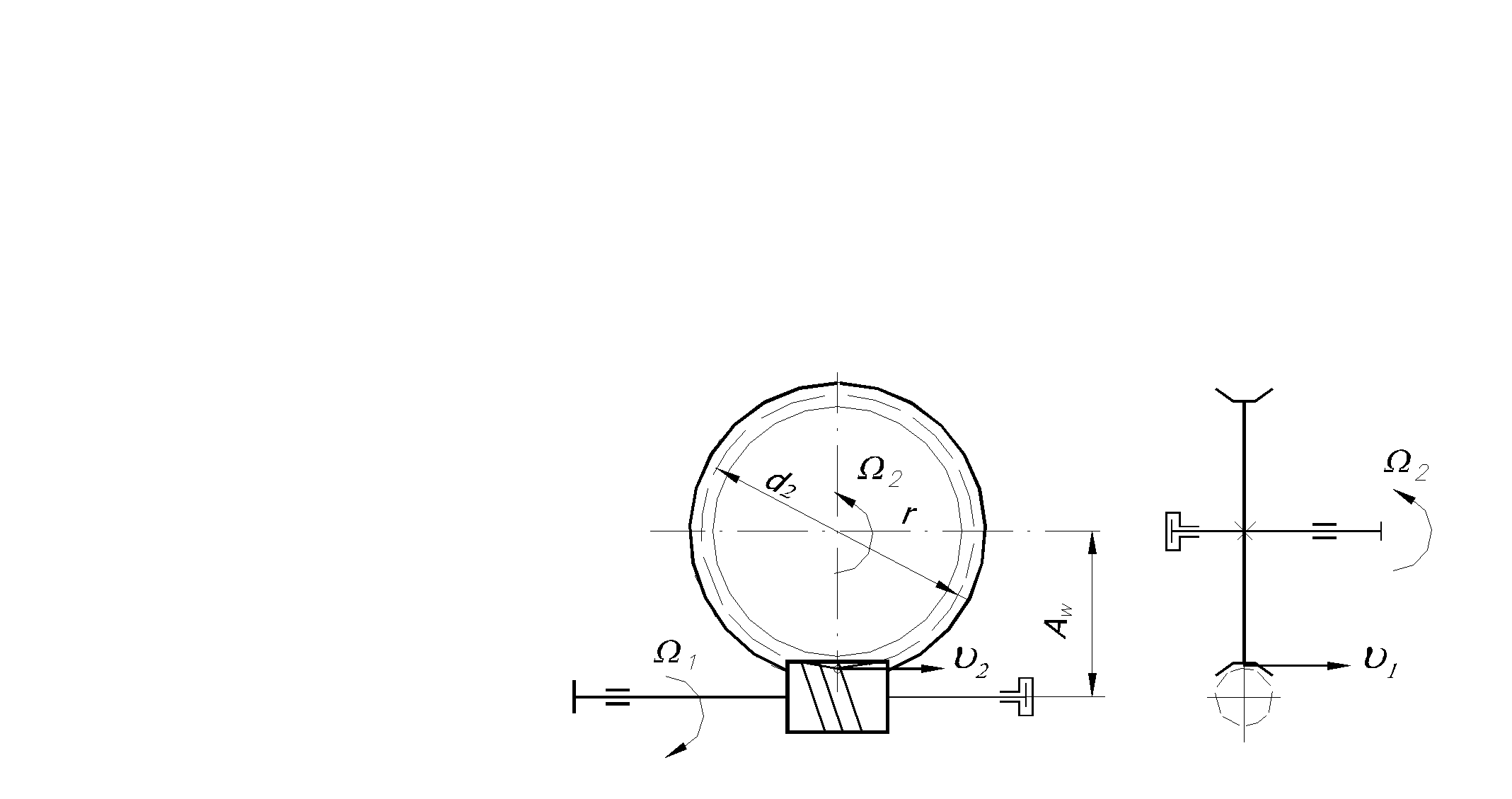
Рис. 5.54 Схема червячной передачи
Червяки различают:
- по форме поверхности, на которой образуется резьба (цилиндрические рис. 5.55,а и глобоидные рис. 5.55,б);
- по форме профиля резьбы (прямолинейный или криволинейный в осевом направлении рис. 5.56).

Рис.5.55
Формы червяков
а) б)
Наиболее распространены цилиндрические червяки. У червяков с прямолинейным профилем в осевом сечении по торцу витки очерчены архимедовой спиралью. Поэтому его называют архимедов червяк (обозначается ZA).

Рис.5.56 Профили резьбы червяка: а) прямолинейный; б) криволинейный
Архимедов червяк подобен ходовому винту с трапецеидальной резьбой. Его можно нарезать на обычных токарных станка или резьбошлифовальных станках.
Работоспособность червячных передач повышается с уменьшением шероховатости поверхности и повышения HRC. Сейчас часто применяют шлифованные высокотвердые червяки при твердости, превышающей 45HRC. Для шлифования требуются специальные шлифовальные круги фасонного профиля. Это затрудняет обработку и снижает точность изготовления. Поэтому архимедовы червяки изготавливают с нешлифованными витками при твердости не превышающей 350НВ.
Для высокотвердых шлифованных витков применяют эвольвентные червяки, имеющие следующие обозначения:
Z1 угол профиля an; ZN1- с прямолинейным профилем витка; ZN2- с прямолинейным профилем впадины; ZK1- цилиндрический, образованный конусом.
Эвольвентные червяки имеют эвольвентный профиль в торцовом сечении и подобны косозубым эвольвентным колесам, у которых число зубьев равно числу заходов червяка. Основные преимущества таких червяков- возможность шлифования витков плоской стороной круга, но для этого необходимы специальные червячно- шлифовальные станки.
Способ изготовления является решающим при выборе профиля нарезки червяка, т.к. при одинаковом качестве изготовления форма профиля мало влияет на работоспособность червячной передачи. Выбор профиля нарезки связан также с формой инструмента для нарезания червячного колеса.
Червячное колесо нарезают червячными фрезами, которые являются копией червяка. Только они имеют режущие кромки и наружный диаметр больше на двойной размер радиального зазора в зацеплении. При нарезании заготовка колеса и фреза совершают такое же взаимное движение, как и червячное колесо и червяк в передаче. Такой метод автоматически обеспечивает сопряженность профилей и обуславливает введение стандарта на основные геометрические параметры червяка:
a- профильный угол сечения зуба (обычно равен 20°);
m= p/2p- осевой модуль ( р- осевой шаг);
z1- число заходов червяка (может быть z1= 1; 2; 4);
q= d1/m.
Значения m и q стандартизированы. (m= 2; 2,5; 3,15…; q= 8; 10; 12,5...)
Кроме того, в справочнике [Анурьев] стандартизированы сочетания параметров: A, m, z2, z1, q, x.
Если червяк будет тонким, то из-за увеличенного прогиба червячного вала нарушится правильность зацепления. Обычно принимают q³ 0,25 z2.
Угол подъема винтовой линии g= arctg (pmz1/pd1)= arctg (z1/q).
Диаметры (см. рис. 5.56) равны:
d1= qm; da1= d1+ 2m; df1= d1- 2,4 m.
Длину нарезанной части червяка b1 определяют по условию использования одновременного зацепления наибольшего числа зубьев с помощью таблицы 5.4.
Таблица 5.4
Расчет длины нарезанной части червяка b1
| x | Расчетные формулы для z1 | |
| 1 и 2 | ||
| -1,0 | b1³ (10,5 +z1)m | b1³ (10,5 +z1)m |
| -0,5 | b1³ ( 8 + 0,06z2)m | b1³ ( 9,5 + 0,09z2)m |
| b1³ ( 11+ 0,06z2)m | b1³ ( 12,5 + 0,09z2)m | |
| +0,5 | b1³ ( 11 + 0,1z2)m | b1³ ( 12,5 + 0,1z2)m |
| +1,0 | b1³ ( 12 + 0,1z2)m | b1³ ( 13 + 0,1z2)m |
| Примечание: 1. При промежуточном значении коэффициента х длину b1 вычисляют по ближайшему пределу х, который дает большее значение b1. 2. Для шлифуемых и фрезеруемых червяков полученную по таблице длину b1 следует увеличить: на 25 мм - при m< 10 мм; на 35- 40 мм при m= 10-16 мм; на 50 мм при m> 16мм. ГОСТ 19650- 74 в приложении предусматривает расчет размеров для контроля осевого профиля. |
При нарезании червячного колеса без смещения параметры его определяются из соотношений:
d2= z2m; da2= d2+ 2m; df2= d2- 2,4m; A= 0,5(q+z2)m. (5-84)
По условию неподрезания должно выполняться неравенство z2³ 28. По условию прочности- z2£ 80.
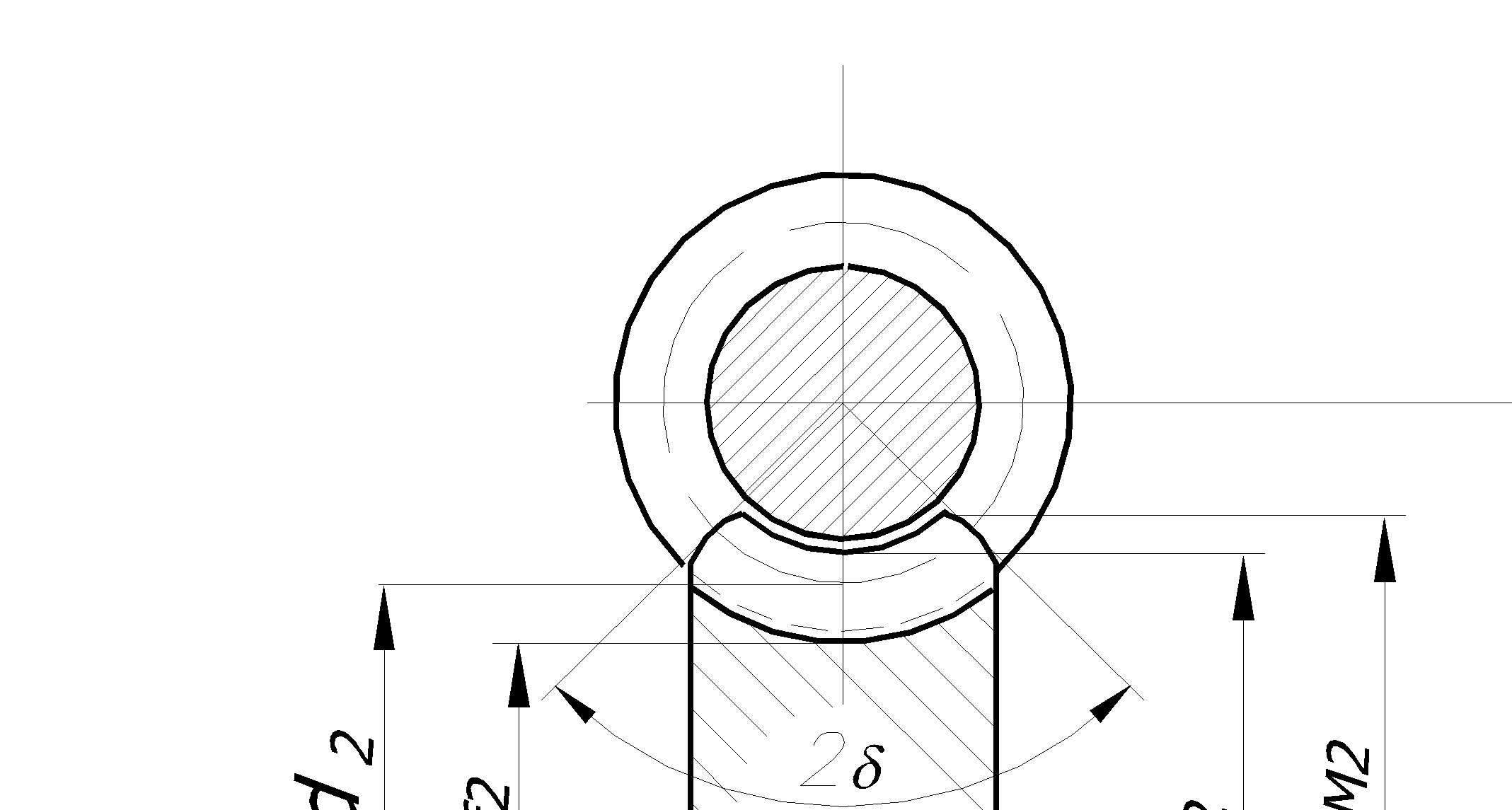
Рис. 5.57
Сечение червяка и червячного колеса
Ширина червячного колеса b2 и наружный диаметр daМ2, соответст-вуют углу обхвата (рис. 5.55) червяка колесом 2d» 90…120° (для силовых передач). При этом sin d= b2/(da1- 0,5 m). Для несиловых передач угол обхвата равен 2d= 45…60° . Часто принимают b2= 0,75 da1 .
В случае нарезания червячных колес со смещением или без смещения используют один и тот же инструмент. Поэтому червяк, являющийся аналогом инструмента, нарезают без смещения.
Смещение при нарезании червячных колес выполняют для округления дробных значений межосевых расстояний до размеров нормального ряда ( Aw= 40; 50; 63;…).
При заданном межосевом расстоянии коэффициент смещения определяется из соотношения
x= Aw/m- 0,5(q+z2).
У червячного колеса со смещением параметры будут определяться следующим образом:
da2= (z2+ 2+ 2x)m; df2= (z2- 2,4+ 2x)m.
Остальные размеры не меняются. Обычно x» ±0,7 мм, хотя в справочнике [5] дается значение -1£ х £+1 мм.
Стандартом установлено 12 степеней точности червячных передач, зависящих от скорости скольжения; обработки червяка и колеса; требований к эксплуатации: 3… 6 – для передач с высокой кинематической точностью; 5…9- для силовых передач (см. табл. 5.5).
Особое внимание уделяют нормам точности монтажа, т.к. ошибки положения колеса и червяка более вредны, чем в других зубчатых передачах.
Таблица 5.5
Выбор степени точности червячной передачи
| Степень точности | Скорость скольжени, м/с | Обработка | Примечание |
| £ 10 | Закалка червяка, шлифовка и полировка. Колесо нарезается шоифрван-ными червячными фрезами. Обкатка под нагрузкой | Подача с повы- шенными скоростями и малым шумом | |
| £ 5 | Твердость червяка £ 350НВ. Нешлифованное колесо наре-зается шлифованной червячной фрезой. Обкатка под нагрузкой. | Средние скорости средние требова-ния к шуму, габа-ритам, точности | |
| £ 2 | Твердость червяка £ 350НВ. Нешлифованное колесо нарезается любым способом. | Низкие скорости, кратковременная работа, ручной при-вод с пониженны-ми требованиями |
При нарезании червячных колес число зубьев не должно содержать общих множителей с числом заходов червяка (z1). Это достигается при сохранении стандартных параметров червяка (z1, m, q) заменой, например, z2= 32 на z2= 31 или z2=33, z2= 36 – на 35 или 37 и т.д..
Для этих передач, чтобы не выходить за пределы допустимых отклонений от передаточного отношения и не иметь x>1, требуется применять специальные резцы.
В червячных передачах окружные скорости перпендикулярно направлены и различны по величине. Здесь в относительном движении начальные цилиндры не обкатываются, а скользят. При одном обороте червяка колесо повернется на угол, охватывающий число зубьев колеса, равное числу заходов червяка, т.е. передаточное отношение равно
i= n1/ n2= z2/ z1. (5-85)
Число заходов червяка выполняет функцию числа зубьев шестерни обычной зубчатой передачи. Так как z1 не велико, то в червячных передачах можно получить большое передаточное отношение (число) i= 10…80 (для силовых), i- до 300 (в кинематических цепях).
Обычно ведущим является червяк. При движении витки червяка скользят по зубьям колеса, как в винтовой паре. Скорость скольжения us является геометрической суммой окружных скоростей u1 и u2
us= u1/ cosg= (u21+ u22)1/2, (5-86)
где u1=p d1n1/60; u2=p d2n2/60.
При проектном расчете
us@ 45*10-4n1Mкр21/3 [м/с].
Причем u2 /u1= tgg.
В червячных передачах u1>u2 и поэтому здесь значительны потери на трение, износ, значительна склонность к заеданию.
Коэффициент полезного действия червячной передачи при ведущем червяке равен
h3= tgg /tg(g+ j), (5-87)
где j- угол трения.
Если ведущим будет колесо, то
h3= tgg /tg(g -j). (5-88)
При g£ j такая передача невозможна.
Коэффициенты трения рекомендуются в таблицах в зависимости от us и j. В качестве предварительных значений можно принять
h3= 0,7…0,75 при z1=1;
h3= 0,75…0,82 при z1=2;
h3= 0,87…0,92 при z1=4.
В червячном зацеплении действуют следующие силы (см. рис. 5.58):
Ft1= Fa2= 2Mкр1/ d1; Ft2= Fa1= 2Mкр2/ d2;
Fr= Ft2 tg a- радиальная сила;
Fn= Ft2 /(cosa*cosg)- нормальная сила,
где Ft1, Ft2- окружные силы, соответственно на червяке и колесе;
Fа1, Fа2- осевые силы, соответственно на червяке и колесе.
Расчет прочности осуществляется по контактным напряжениям и по напряжениям изгиба.
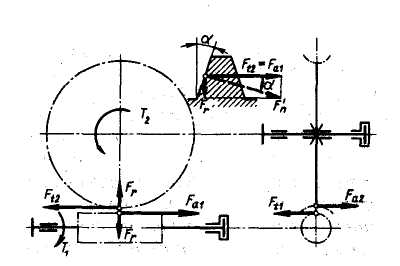
Рис. 5.58
Силы в червячной передаче.
Контактные напряжения определяются на базе формулы
sH= 0,418 (qчЕпр/ rпр)1/2.
В архимедовом червяке r1= ¥ (прямая) и поэтому
r-1пр@ 2 cos2g/ (d2cosa).
По аналогии с косозубой передачей удельная нагрузка для червячной передачи
qy= FnKп/ lS= 2Mкр2KH/(d2d1deazcosa), (5-89)
гдеlS= d1deaz/cosa- суммарная длина линии контакта; ea=1,8…2,2 - торцовый коэффициент перекрытия в средней плоскости червячного колеса; z= 0,75 - коэффициент, учитывающий уменьшение длины контактной линии из-за соприкосновения не по полной дуге обхвата.
В итоге
sH= 1,18 [EnpMкр2КНcos2g/( d22d1deaz sin2a)]1/2 , (5-90)
Aw= 0,625 (q/z2+ 1) { EnpMкр2 /([sH]2q z-12)}1/3. (5-91)
Расчет червячной передачи выполняется разными методами. Здесь расчет производится в соответствии с рекомендациями Анурьева В.И.[5].
По этому методу, приняв q/z2= 0,33 и используя формулу (5-91) оцениваем межцентровое расстояние. Затем c учетом задания из таблицы в [5] определяем стандартное сочетание: Aw; z’2/z1; m; q; x; u.
Затем вычислям z2= z’2+1 и x= A/m- 0,5(q+ z2).
После этого определяются: d2= z2m; d1= qm; tgg= z1/q.
Далее при угле обхвата 2d= 100° вычисляется диаметр выступов червяка
da1= d1+ 2m
и ширина червячного колеса
b2@0,75da1.
Длину нарезанной части червяка определяем по методике Анурьева (см. табл. 5.4).
По скорости скольжения uск= pd1n1/(6*104*cosg) на основании рекомендаций Анурьева выбираем материал червяка и колеса.
Определяем затем торцовый коэффициент перекрытия
ea= [(0,03z22+ z2+ 1)1/2- 0,17z2+ 2,9]/2,95. (5-92)
Приняв коэффициент, учитывающий длину контактной линии, равным z= 0,75, по формуле (5-90) определяем контактные напряжения, которые не должны превышать допустимые.
По напряжениям изгиба расчитываем только зубья колеса. Из-за их переменного сечения введен в рассмотрение коэффициент формы зуба YF, который для z2= 20 равен 1,98; для z2= 32 - 1,71; для z2= 40 - 1,55; для z2= 60 - 1,40.
Определив далее окружную силу Ft2= 2Mкр2/d2 для нормального модуля mn= m*cosg , рассчитаем напряжения изгиба
sF= 0,7YFFtKF/(b2mn), (5-93)
которые не должны превышать допустимые значения.
Затем уточняем к.п.д.
h= tgg/tg(g+ j),
где j выбирается из справочника.
Планетарные передачи.
Это передачи, содержащие зубчатые колеса с перемещающи-мися осями. Состоят из центрального колеса «а» с наружными зубьями, центрального колеса с «b» с внутреними зубьями, водила «h» и сателлита «q».
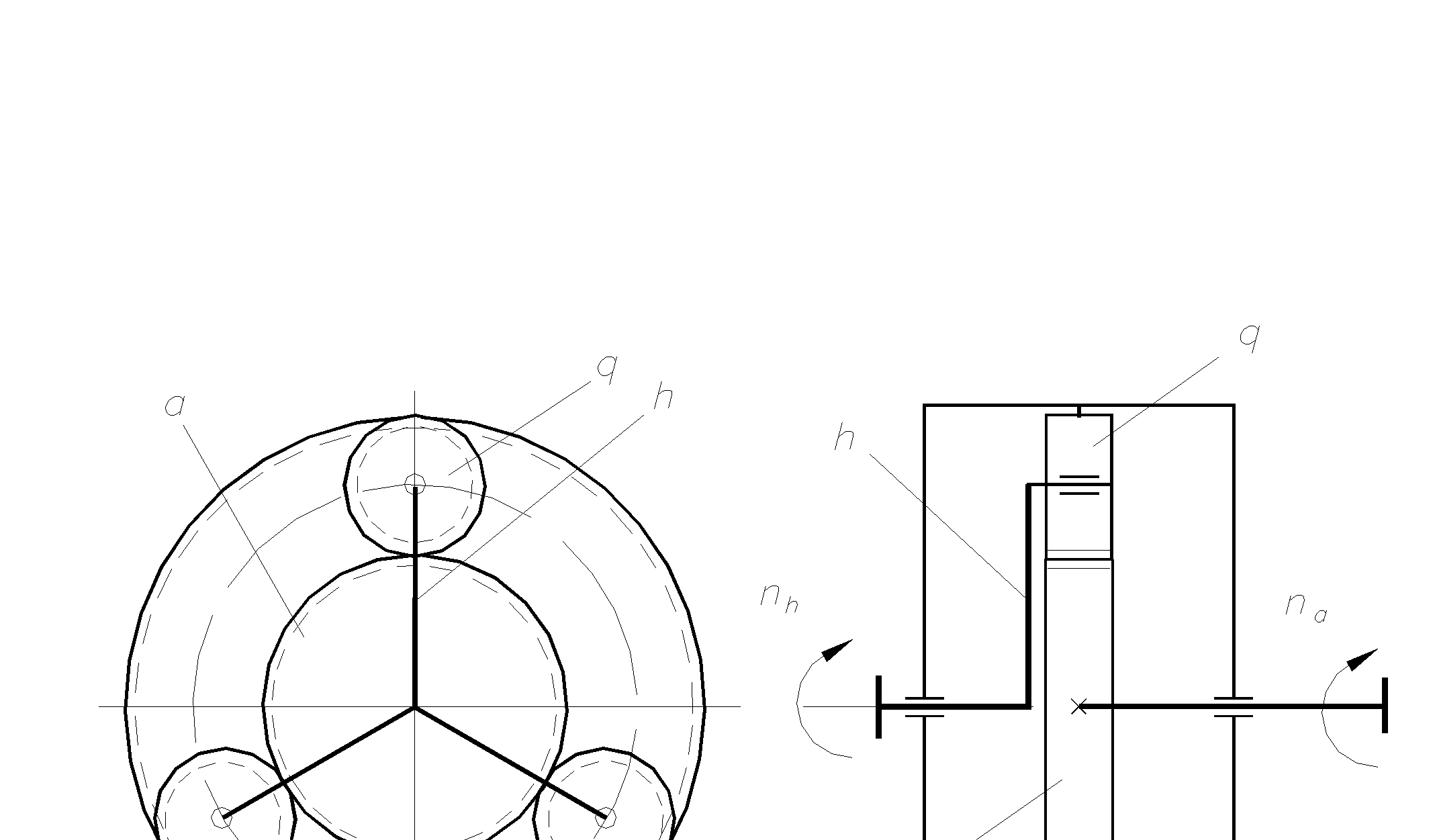
а) б) в)
Рис. 5. 59 Схемы планетарных редукторов.
Сателлиты (рис.5.59,а) вращаются вокруг своих осей и вместе с осью вокруг центрального колеса. Поэтому передача и называется планетарной.
При неподвижном колесе «b» (рис. 5.59,а, б) движение может передаваться от «а» к «h». В случае неподвижного водила h (рис. 5.59, в) движение передается от a к b или от b к a. При всех свободных звеньях одно движение можно раскладывать на два или два соединить в одно, например, от b к a, от h к a, от h к b и т.д. В этом случае передачу называют дифференциальной.
Широкие кинематические возможности этой передачи являются одним из основных ее достоинств, и позволяет использовать передачу как редуктор с постоянным передаточным отношением, как коробку скоростей, передаточное отношение которой изменяют поочередным торможением различных звеньев; как дифференциальный механизм.
Второе достоинство- компактность и малая масса.
Снижение размеров и массы (в 2- 4 раза) объясняется разделением мощности по нескольким потокам (в зависимости от числа сателлитов). При этом: а) нагрузка на зубья уменьшается в несколько раз; б) внутреннее зацепление (q в b) обладает повышенной нагрузочной способностью, т.к. у него больше приведенный радиус кривизны в зацеплении; в) планетарный принцип позволяет получить более высокие передаточные отношения (свыше 1000) без применения многоступенчатых передач; г) имеет место малая нагрузка на опоры из-за симметричного расположения сателлитов.
К недостаткам относятся повышенные требования к точности изготовления и монтажа.
При исследовании кинематики планетарных передач широко пользуются методом остановки водила- метод Виллиса. Всей передаче мысленно сообщается вращение с частотой вращения водила, но в обратном направлении. При этом водило как бы затормаживается, а все другие звенья освобождаются. Получается обращенный механизм, представляющий собой простую передачу, где движение передается от a к b через паразитные колеса q.
Частоты вращения зубчатых колес обращенного механизма равны разности прежних частот вращения и частоты вращения водила. Введем обозначение передаточное отношение от a к h при неподвижном b.
ihab= (na- nh)/(nb- nh)=- zh/za. (5-94)
В планетарной передаче существенное значение имеет знак передаточного отношения. На рис. 5.59,а колеса a и b вращаются в разных направлениях. Поэтому ihab< 0.
Если в формуле (5-94) nb= 0, то
(na- nh)(-nh)= -zb / za .
Откуда следует
na/nh+ 1= -zb/ za . (5-95)
То есть
ibah= 1+ zb/ za.
Частоту вращения сателлита можно определить из равенства
(na- nh)/(nq- nh)= - zq/za= ihbq. (5-96)
При заданных na и nh определяют nq или (nq- nh), как частоту вращения сателлита относительно водила или относительно своей оси.
Силы в зацеплении (рис. 5 .60 ).
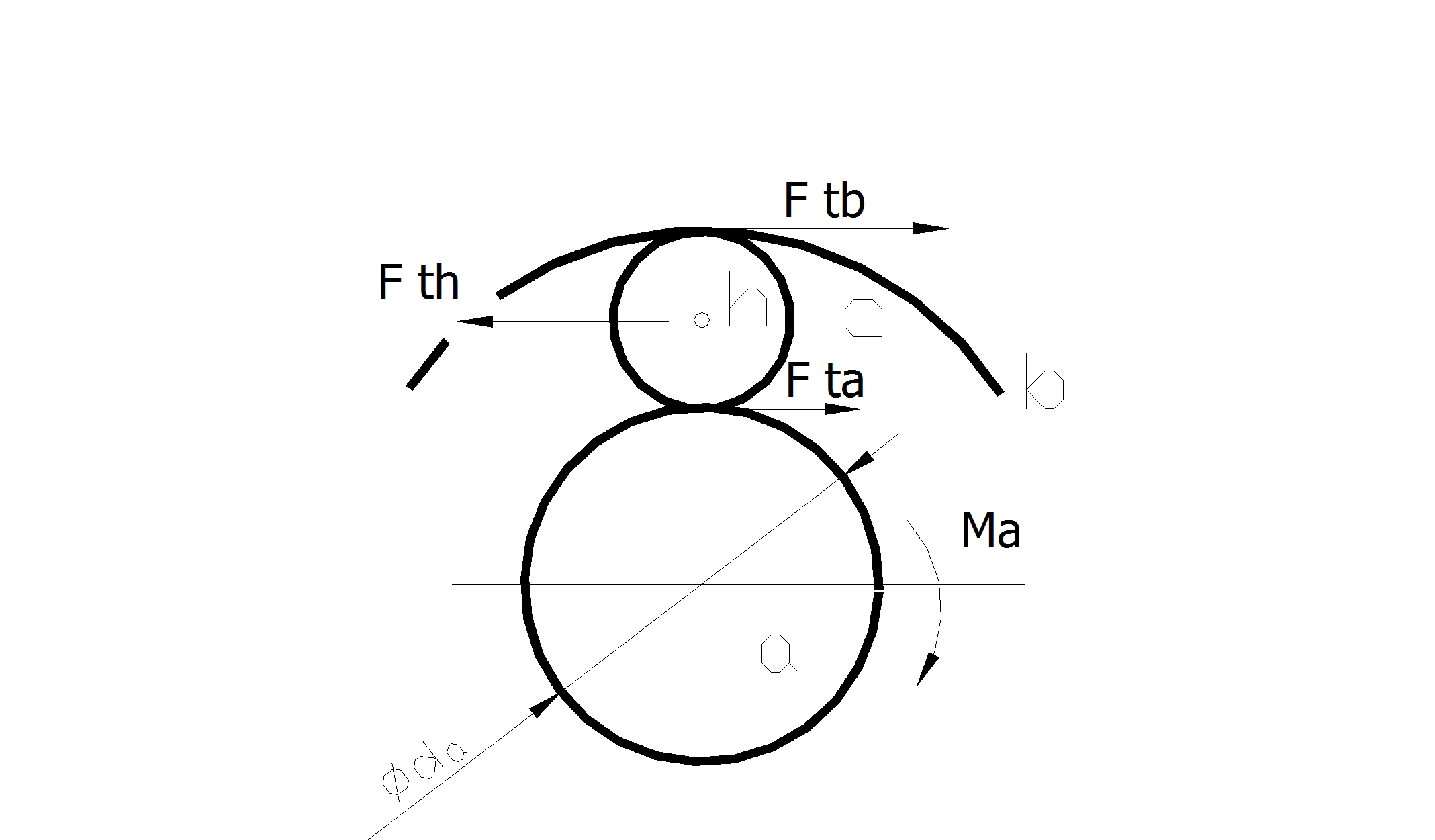
Рис.5.60
Силы в зацеплении
Fta= Ftb; Fth= -2Fta , (5-97)
где Fta= 2MaKc/(dac); Кс- коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами; с- число сателлитов.
Радиальные и осевые нагрузки при известной окружной силе определяют также как и простых передачах. Коэффициент Кс зависит от точности изготовления и числа сателлитов.
Из структурного анализа планетарной передачи, выполняемого в теории механизмов, установлено, что если центральное колесо а сделать самоустанавливающимся, то можно существенно снизить неравномерность распределения нагрузки между сателлитами. Для этого применяют соединение колеса с валом посредством зубчатой муфты. В этом случае Кс= 1,1…1,2. В противном случае Кс= 1,2…2.
При известных окружных силах вращающие моменты равны Mi= Ftiri. В общем виде для определения сил и моментов используют структурную схему планетарной передачи, как трехзвенного механизма.
По условию равновесия
Ma+ Mb+ Mh= 0. (5-98)
По условию сохранения энергии
MaWa+ MbWb+ MhWh = 0. (5-99)
Следует иметь в виду, что в этой формуле не учтены потери на трение.
Если известны частоты вращения и известен один момент, то, например, при ведущем a и закрепленном b, когда Wb= 0, с учетом известного к.п.д. hbah крутящий момент будет
Mh= - Mahbah Wa/Wh. (5-100)
Из (5-98) найдем
Mb= Ma(hbah Wa/Wh – 1). (5-101)
Потери на трение yп в подшипниках меньше, чем у простой передачи, т.к. при симметричном расположении сателлитов силы в зацеплении уравновешиваются и не нагружают валы и опоры.
Гидравлические потери yг в планетарных передачах при смазке погружением сателлитов в масляную ванну могут быть значительно больше, чем у простой передачи. Здесь рекомендуют неглубокое погружение колес в масляную ванну, а при больших скоростях применять смазку разбрызгиванием или струйную.
Потери на трение в зацеплении yз в планетарных передачах сравнимы с простыми передачами.
Выбор типа планетарной передачи.
Существует большое количество типов таких передач. Самое широкое применение получила схема на рис.5.59,а с рациональными пределами передаточных отношений ibah= 3…9 (b закреплено). При этом к.п.д. составляет h= 0,97…0,99.
В случае больших передаточных отношений в силовых передачах следует применять 2-х и 3-х ступенчатые простые передачи.
В планетарных передачах находят применение цилиндрические, конические и даже червячные колеса. Зубья могут быть прямыми, косыми, с коррекцией или без нее.
Расчет на прочность производят для каждого зацепления. Поскольку внутреннее зацепление по своим свойствам прочнее наружного, то при одинаковых материалах достаточно рассчитывать только зацепления центрального колеса а и сателлитов q.
При расчете на изгиб используют формулу (5-41). Для расчета по контактным напряжениям ранее приведенная формула модернизирована
d1= 1,35{EnpMкр1KHb(Kcc-1)(u+1)/(u[sH]2ybd)}1/3. (5-102)
Для планетарной передачи рекомендуют ybd= bw/ d1£ 0,75.
Выбор числа зубьев.
При заданном передаточном отношении число зубьев определяют с помощью ранее приведенных формул в зависимости от типа передачи.
Дата добавления: 2015-02-23; просмотров: 2872;
