Гилерболоидные зубчатые передачи.
Волновая зубчатая передача — механизм, содержащий зацепляющиеся между собой гибкое и жесткое зубчатые колеса и обеспечивающий преобразование и передачу движения благодаря деформированию гибкого колеса (рис. 19.1).
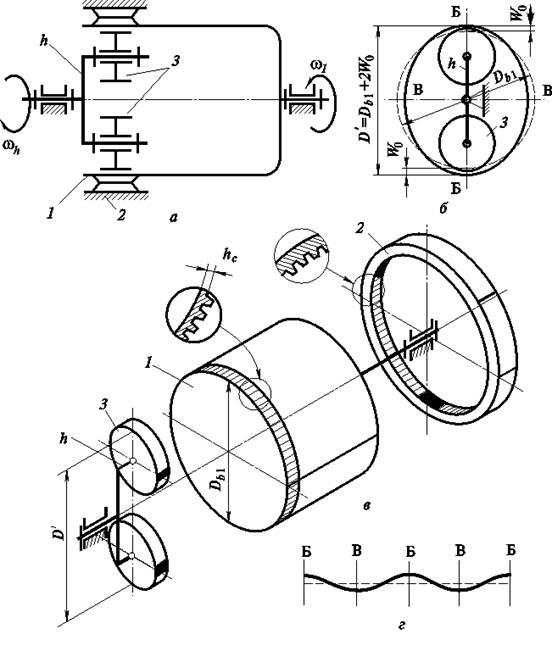
Рис. 19.1
Волновая зубчатая передача (ВЗП) состоит из трех основных элементов: гибкого колеса 1 (рис. 19.1, а, б, в), жесткого колеса 2 и генератора волн h. Ее можно рассматривать как конструктивную разновидность планетарной передачи с внутренним зацеплением, характерной особенностью которой является использование сателлита (гибкого колеса), деформируемого в процессе передачи движения. Гибкое зубчатое колесо представляет собой тонкостенную оболочку, один конец которой соединен с валом и сохраняет цилиндрическую форму, а на другом нарезан зубчатый венец с числом зубьев 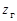 . При сборке этот конец оболочки деформируется на
. При сборке этот конец оболочки деформируется на 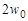 генератором волн. Контур деформированного гибкого колеса образует относительно недеформированного две волны деформации (рис. 19.1, г). Размер по сечению Б – Б называют большой осью, а по В – В — малой осью кривой деформации. В зоне большой оси деформации происходит зацепление зубьев гибкого и жесткого колес. Для обеспечения симметрии нагружения волновой зубчатой передачи обычно используют две волны деформации и четные числа зубьев колес, которые связаны соотношением
генератором волн. Контур деформированного гибкого колеса образует относительно недеформированного две волны деформации (рис. 19.1, г). Размер по сечению Б – Б называют большой осью, а по В – В — малой осью кривой деформации. В зоне большой оси деформации происходит зацепление зубьев гибкого и жесткого колес. Для обеспечения симметрии нагружения волновой зубчатой передачи обычно используют две волны деформации и четные числа зубьев колес, которые связаны соотношением 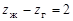 .
.
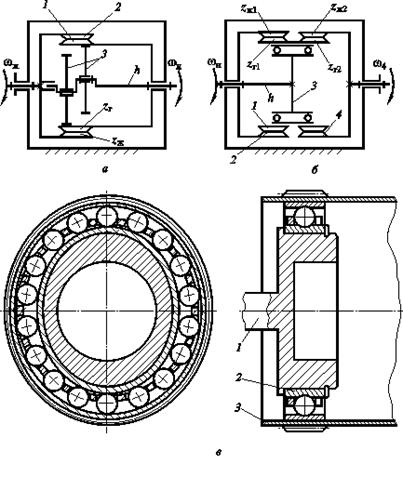
Рис. 19.2
Гибкое колесо 1 поджато к жесткому 2 роликами 3, расположенными на водиле h. Такой генератор называют роликовым. Роликовый генератор волн может быть преобразован в дисковый генератор волн при значительном увеличении диаметров роликов 3 (рис. 19.2, а) и расположении их в параллельных плоскостях. Чтобы задать зубчатому венцу гибкого колеса определенную принудительную форму деформации, генератор нужно выполнить в виде симметричного кулачка специального профиля. Такой генератор называют кулачковым (рис. 19.2, в). На кулачок 1 напрессовывают гибкий подшипник 2, чтобы уменьшить трение между гибким колесом 3 и генератором волн. Дисковые и кулачковые генераторы волн применяют в высоко нагруженных передачах. Кроме механических генераторов волн применяют также электромагнитные, пневматические и гидравлические генераторы.
Кинематика волновой передачи. При вращении генератора волн обе волны деформации перемещаются по периметру гибкого колеса. В результате каждый зуб гибкого колеса за один оборот генератора волн дважды входит в зацепление с зубьями жесткого колеса. Если числа зубьев колес равны 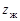 и
и  , а угловые шаги
, а угловые шаги  и
и 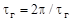 , то передаточное отношение такой передачи можно подсчитать следующим образом. При остановленном жестком колесе после полного оборота генератора волн
, то передаточное отношение такой передачи можно подсчитать следующим образом. При остановленном жестком колесе после полного оборота генератора волн 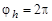 вал гибкого колеса повернется в противоположном движению генератора направлении на угол, равный
вал гибкого колеса повернется в противоположном движению генератора направлении на угол, равный 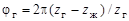 .
.
Переходя от углов поворота к угловым скоростям, получаем передаточное отношение ВЗП от генератора волн к гибкому колесу при неподвижном жестком:
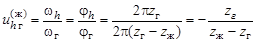 . (19.1)
. (19.1)
В ВЗП с остановленным гибким колесом при повороте генератора волн на угол 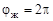 жесткое колесо повернется в том же направлении на угол
жесткое колесо повернется в том же направлении на угол 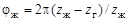 . В этом случае передаточное отношение от генератора волн к жесткому колесу при неподвижном гибком
. В этом случае передаточное отношение от генератора волн к жесткому колесу при неподвижном гибком
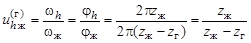 . (19.2)
. (19.2)
Волновая передача может быть двухступенчатой (рис. 19.2, б). В этом случае гибкое колесо 1 выполняется в виде кольца с двумя зубчатыми венцами 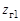 и
и 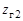 , которые входят в зацепление с жесткими колесами 2 и 4, имеющими соответственно
, которые входят в зацепление с жесткими колесами 2 и 4, имеющими соответственно 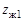 и
и 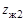 зубьев. Если жесткое колесо 2 неподвижно, то движение от вала генератора волн преобразуется с помощью двух волновых зацеплений и передается на выходной вал, соединенный с жестким колесом 4. Передаточное отношение двухступенчатой ВЗП определяется формулой
зубьев. Если жесткое колесо 2 неподвижно, то движение от вала генератора волн преобразуется с помощью двух волновых зацеплений и передается на выходной вал, соединенный с жестким колесом 4. Передаточное отношение двухступенчатой ВЗП определяется формулой
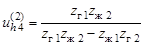 . (19.3)
. (19.3)
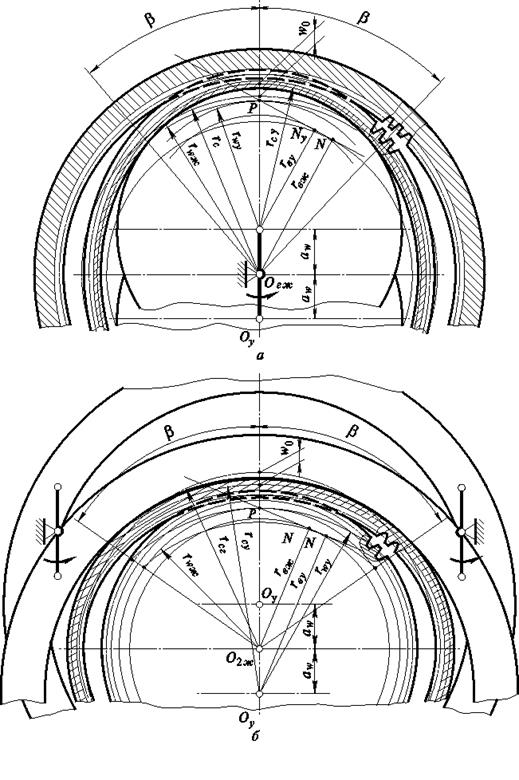
Особенности волнового зацепления. Гибкое колесо ВЗП при его нагружении изменяет свою начальную форму. Это происходит из-за наличия зазоров и упругости элементов, взаимодействующих с гибким колесом. Изменение формы гибкого колеса 1 ограничено с внешней стороны жестким колесом 2, а с внутренней генератором волн h. Гибкое колесо, опирающееся на генератор волн в пределах участков постоянной кривизны 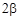 (рис. 19.3), стремится принять форму жесткого колеса. С увеличением момента закручивающего гибкое колесо зоны выбранных зазоров в зацеплении увеличиваются, что приводит к увеличению числа пар зубьев в зацеплении. Благодаря многопарности зацепления (нагрузку могут передавать до 40 % всех пар зубьев) нагрузочная способность ВЗП выше, чем планетарной. КПД волновой передачи также выше, потому что в зацеплении зубья почти не перемещаются при прилегании гибкого колеса к жесткому. При стальных гибких колесах в одноступенчатых волновых передачах можно получить передаточное отношение 60 – 320, а КПД равным 0,85...0,80. Двухступенчатые ВЗП обеспечивают передаточные отношения от
(рис. 19.3), стремится принять форму жесткого колеса. С увеличением момента закручивающего гибкое колесо зоны выбранных зазоров в зацеплении увеличиваются, что приводит к увеличению числа пар зубьев в зацеплении. Благодаря многопарности зацепления (нагрузку могут передавать до 40 % всех пар зубьев) нагрузочная способность ВЗП выше, чем планетарной. КПД волновой передачи также выше, потому что в зацеплении зубья почти не перемещаются при прилегании гибкого колеса к жесткому. При стальных гибких колесах в одноступенчатых волновых передачах можно получить передаточное отношение 60 – 320, а КПД равным 0,85...0,80. Двухступенчатые ВЗП обеспечивают передаточные отношения от 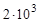 до
до 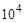 и более при КПД от 0,7 до 0,1.
и более при КПД от 0,7 до 0,1.
|
Многопарность и многозонность волнового зацепления приводят к значительному усреднению ошибок изготовления и сборки, в результате чего обеспечивается высокая кинематическая точность ВЗП.
Относительно небольшая величина радиальной деформации гибкого колеса позволяет выполнить его в виде колоколообразной оболочки и изготовить герметичные ВЗП, передающие вращение через герметичную перегородку без подвижных уплотнений.
Наиболее ответственные детали ВЗП — гибкий подшипник и гибкое колесо. Гибкое колесо имеет тонкостенное донышко, допускающее осевые перемещения торца цилиндрической оболочки при ее деформировании с другого края. Длину гибкого колеса выбирают от 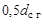 до
до 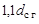 , где
, где 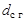 — диаметр недеформированной серединной поверхности гибкого колеса. Толщину
— диаметр недеформированной серединной поверхности гибкого колеса. Толщину 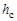 гибкого колеса под зубчатым венцом выбирают примерно равной
гибкого колеса под зубчатым венцом выбирают примерно равной 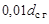 .
.
Методика проектирования ВЗП. Существует несколько методов расчета геометрических параметров волновых зубчатых передач. Настоящая методика, разработанная на кафедре теории механизмов и машин МГТУ им. Н.Э. Баумана, основывается на предположении, что конструкции генераторов волн рассматриваемых передач обеспечивают постоянную кривизну серединного слоя деформированного гибкого колеса в пределах зон зацепления, ограниченных центральными углами 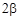 (см. рис. 19.3, а). Вне этих зон гибкое колесо имеет свободную форму деформации. На участке постоянной кривизны зацепление в волновой передаче рассматривается как внутреннее эвольвентное зацепление жесткого колеса с числом зубьев
(см. рис. 19.3, а). Вне этих зон гибкое колесо имеет свободную форму деформации. На участке постоянной кривизны зацепление в волновой передаче рассматривается как внутреннее эвольвентное зацепление жесткого колеса с числом зубьев 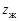 и условного, имеющего параметры гибкого и расчетное число зубьев
и условного, имеющего параметры гибкого и расчетное число зубьев 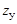 .
.
Исходными параметрами для расчета являются передаточное отношение передачи, ее схема, номинальный крутящий момент на выходном валу, частота вращения генератора волн, срок службы передачи, прочностные характеристики гибкого колеса. Проектировочный расчет заключается в определении диаметра серединной поверхности гибкого колеса по изгибной прочности, из расчета на выносливость или из расчета заданного коэффициента крутильной жесткости [16]. Больший из вычисленных диаметров берется за основу для определения модуля зацепления 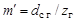 , который округляется до ближайшего стандартного значения.
, который округляется до ближайшего стандартного значения.
Делительные диаметры колес и толщина 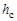 обода гибкого колеса под зубчатым венцом определяются по формулам
обода гибкого колеса под зубчатым венцом определяются по формулам
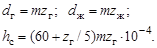 (19.4)
(19.4)
Основным варьируемым параметром является относительная радиальная деформация гибкого колеса по большой оси:
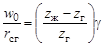 , (19.5)
, (19.5)
где 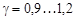 — коэффициент относительной радиальной деформации.
— коэффициент относительной радиальной деформации.
Расчетное число зубьев условного колеса равно
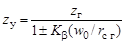 . (19.6)
. (19.6)
В формуле (19.6), как и во всех последующих, содержащих двойные знаки арифметических действий, верхний знак относится к внутреннему деформированию гибкого колеса дисковым или кулачковым генератором волн, нижний — к внешнему деформированию кольцевым генератором (рис. 19.3, б):
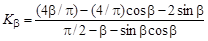 , (19.7)
, (19.7)
где 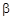 — угловая координата участка постоянной кривизны (
— угловая координата участка постоянной кривизны ( 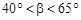 ).
).
Далее определяем радиус серединной окружности деформированного гибкого колеса (см. рис. 19.3):
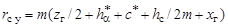 , (19.8)
, (19.8)
где 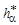 ,
, 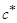 — параметры исходного контура;
— параметры исходного контура; 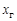 — коэффициент смещения исходного контура:
— коэффициент смещения исходного контура:
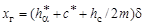 , (19.9)
, (19.9)
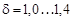 — коэффициент смещения.
— коэффициент смещения.
При изменении величин 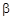 ,
, 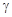 и
и 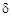 в указанных диапазонах их возможного изменения можно провести оптимизацию качества зацепления. Целевой функцией является теоретический коэффициент перекрытия.
в указанных диапазонах их возможного изменения можно провести оптимизацию качества зацепления. Целевой функцией является теоретический коэффициент перекрытия.
Радиус серединной окружности недеформированного гибкого колеса
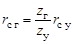 . (19.10)
. (19.10)
Межосевое расстояние передачи, равное эксцентриситету установки деформирующих дисков, равно
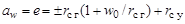 . (19.11)
. (19.11)
Тогда угол зацепления волновой передачи
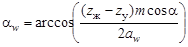 . (19.12)
. (19.12)
Жесткое колесо в передачах с дисковым или кулачковым генератором внутреннего деформирования, имеющее внутренние зубья, обрабатывается долбяком с числом зубьев 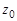 . Угол станочного зацепления жесткого колеса и долбяка
. Угол станочного зацепления жесткого колеса и долбяка
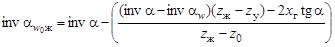 , (19.13)
, (19.13)
и коэффициент смещения жесткого колеса
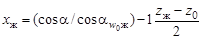 . (19.14)
. (19.14)
Остальные параметры и исполнительные размеры элементов волновой передачи рассчитывают так же, как зубчатой передачи внутреннего эвольвентного зацепления.
Области применения ВЗП. Отмеченные достоинства волновой передачи определяют наиболее рациональные области ее применения: силовые и кинематические приводы общего назначения с большим передаточным отношением, задающие и исполнительные механизмы повышенной кинематической точности, быстродействующие приводы систем автоматического управления и регулирования, электромеханические приводы промышленных роботов, приводы для передачи движения в герметизированное пространство в химической, атомной и космической технике.
Гилерболоидные зубчатые передачи.
Гиперболоидной зубчатой передачей называется передача со скрещивающимися осями, оксоидами зубчатых колес которой являются однополостные гиперболоиды вращения (см. рис 21.1), оси которых не пересекаются.
Для обеспечения точечного касания линий зубьев можно применить более простые по форме поверхности, чем гиперболоиды вращения, что упрощает изготовление зубчатых колес. Например, круглые цилиндры, касающиеся друг друга только в одной точке, лежащей на линии кратчайшего расстояния между осями колес, или конусы с несовпадающими вершинами.
Гиперболоидная зубчатая передача, у зубчатых колес которой начальные поверхности - круглые цилиндры, называется винтовойзубчатой передачей. Если в качестве начальных поверхностей зубчатых колес применить конусы с несовпадающими вершинами, то получим гипоиднуюзубчатую передачу.
Червячнаяпередача представляет собой гиперболоидную передачу, у зубчатых колес которой начальные и делительные поверхности отличны от конических и шестерня - червяк 1 (см. рис. 13.3, е) имеет винтовые зубья, а второе звено 2 называется червячным колесом.
Винтовая зубчатая передача(рис. 21.1) представляет собой гиперболоидную передачу, у зубчатых колес которой начальные поверхности сливающиеся с делительными - цилиндрические, а оси скрещиваются под произвольным углом 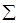 . В большинстве случаев применяют передачи с межосевым углом
. В большинстве случаев применяют передачи с межосевым углом 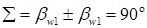 где
где 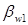 и
и 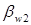 углы наклона линий зубьев (винтовых линий) по начальным цилиндрам; верхний знак соответствует одноименному направлению винтовых линий, нижний - разноименному.
углы наклона линий зубьев (винтовых линий) по начальным цилиндрам; верхний знак соответствует одноименному направлению винтовых линий, нижний - разноименному.
В отличии от косозубых цилиндрических передач для винтовых зубчатых колес не является обязательным равенство углов наклона винтовых линий и разноименность их направлений.
|
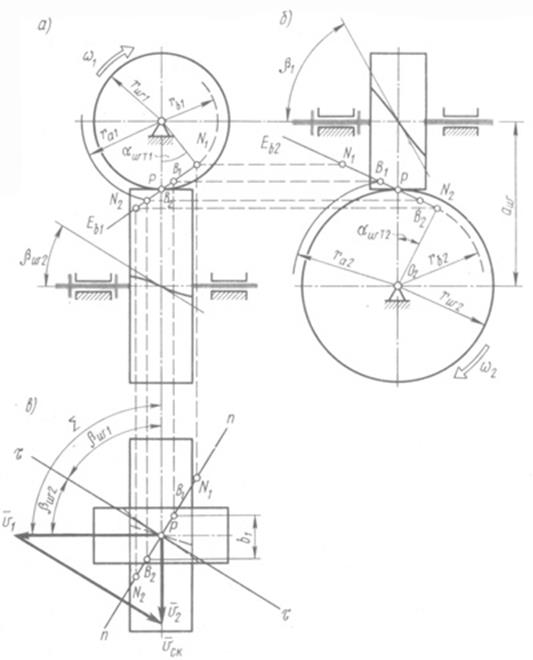 |
На рис 21.1 показаны три проекции начальных цилиндров винтовой передачи с радиусами rw1 и rw2 и концентричные им основные цилиндры с радиусами rв1 и rв2. Винтовые линии на начальных цилиндрах показаны в положении касания в точке Р - полюсе зацепления, n-n - нормаль к ним. Общая касательная
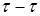 составляет с осями колес соответственно углы
составляет с осями колес соответственно углы 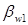 и
и 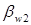 сумма которых равна
сумма которых равна 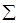 .
.
Касательно к основным цилиндрам через полюс зацепления Р проходят образующие плоскости Ee1 и Ев2, в которых расположены прямолинейные образующие, боковые поверхности зубьев, составляющие углы 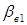 и
и 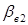 , с осями колес. В передачах со скрещивающимися осями производящие плоскости пересекаются по прямой, представляющей собой геометрическое место точек контакта боковых поверхностей зубьев, называемых линией зацепления. Предельные точки N1 и N2 линии зацепления отмечены на основных цилиндрах. Активная длина линии зацепления определяется точками В1 и В2 пересечения линии зацепления поверхностями цилиндров вершин зубьев колес с радиусами
, с осями колес. В передачах со скрещивающимися осями производящие плоскости пересекаются по прямой, представляющей собой геометрическое место точек контакта боковых поверхностей зубьев, называемых линией зацепления. Предельные точки N1 и N2 линии зацепления отмечены на основных цилиндрах. Активная длина линии зацепления определяется точками В1 и В2 пересечения линии зацепления поверхностями цилиндров вершин зубьев колес с радиусами 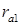 и
и 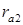 .
.
Для колес 1 и 2, вращающихся соответственно с угловыми скоростями 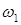 и
и 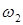 на рис. 12.10, в представлен план скоростей, построенный при расположении колеса 1 над колесом 2. Исходя из равенства нормальных составляющих
на рис. 12.10, в представлен план скоростей, построенный при расположении колеса 1 над колесом 2. Исходя из равенства нормальных составляющих 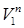 , окружных скоростей в точке касания начальных цилиндров, справедливо соотношение:
, окружных скоростей в точке касания начальных цилиндров, справедливо соотношение:
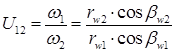 (21.1)
(21.1)
Из этого следует положение, характерное для винтовых передач: заданное передаточное отношение U12 можно осуществить, выбирая произвольно отношение 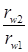 или
или 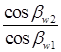
Если передача образована винтовыми колесами с правым и левым направлением винтовых линий, то знак в равенстве (21.1) будет отрицательным. Формула (21.1) свидетельствует о многозначности решения задачи осуществления заданного передаточного отношения. Из ряда вариантов следует выбрать тот, который дает лучшие качественные показатели зацепления винтовых линий.
В нормальном сечении шаг и модуль колес винтовой передачи одинаковы, поэтому для передачи, у которой начальные и делительные цилиндры сливаются, имеем р = pwl = pw2 = p = 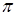
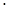 т; в торцевых же сечениях модули разные:
т; в торцевых же сечениях модули разные: 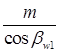 и
и 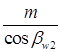 .
.
Радиусы делительных и начальных цилиндров определяются по формулам:
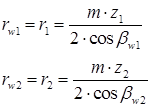 (21.2)
(21.2)
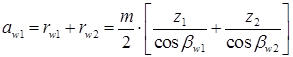 (21.3)
(21.3)
Все исполнительные размеры определяются по формулам для косозубых колес (см. лекцию 16).
Скорость скольжения боковых поверхностей зубьев в направлении общей касательной к винтовым поверхностям зубьев для контактной точки, совпадающей с полюсом Р (см.рис.21.1) определяются по формуле:
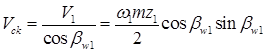 (21.4)
(21.4)
Вследствие точечного контакта рабочих поверхностей рассматриваемых передач в сочетании со значительным скольжением их нагрузочная способность мала, поэтому винтовые передачи применяют большей частью в приборостроении.
|
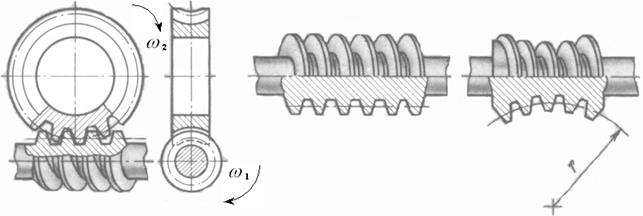
Червячная зубчатая передача,являющаяся частным случаем гиперболоидной, используется для передачи вращения между скрещивающимися осями с постоянным отношением скоростей звеньев. В подавляющем большинстве случаев угол скрещивания осей выбирается равным 90°. Известны две разновидности червячного зацепления: а) с цилиндрическим червяком (рис. 21.1, б) (поверхность витков такого червяка является геликоидом); б) с глобоидным червяком (рис. 21.2, в) по форме которого зацепление названо глобоидным. В зависимости от направления линии витка червяка червячные передачи бывают с правым и левым направлением линии витка. В зависимости от формы винтовой поверхности червяка передачи бывают с архимедовым (архимедова спираль), конволютным (удлиненная или укороченная эвольвента) или эвольвентным червяком. Червячное колесо есть косозубое колесо с зубчатым венцом специальной горловидной формы, охватывающим червяк и образующим как бы бесконечную гайку. Работу червячной передачи можно представить как непрерывное ввинчивание винта -червяка - в бесконечную гайку - червячное колесо. Червяк, как правило, является ведущим звеном, а червячное колесо - ведомым. Обратная передача движения (за редким исключением) неосуществима из-за эффекта самоторможения. На рис. 21.2, а представлена червячная зубчатая передача с червяком цилиндрической формы.
В отличие от винтовой передачи, составленной из цилиндрических колес с винтовыми зубьями, в червячном зацеплении поверхности зубьев имеют не точечное, а линейное касание, что позволяет использовать такое зацепление для передачи значительных нагрузок. Другим важным достоинством червячной передачи является возможность обеспечения большого передаточного отношения от 20 до 500. Кроме того, червячная передача, как и другие косозубые передачи, обладает высокой плавностью и бесшумностью вращения.
Однако червячные передачи имеют и существенные недостатки:
1. КПД этих передач по сравнению с КПД других многочисленных передач весьма низок - 0,5-0,7;
2. повышенное скольжение контактирующих профилей вызывает их износ и требует применения для венцов червячных колес антифрикционных материалов;
3. значительное выделение теплоты в зоне зацепления червяка с колесом требует интенсивного охлаждения передачи;
4. большое осевое усилие на червяк требует постановки червяка на подшипники, способные воспринимать большие осевые реакции.
Нарезание червяков и червячных колес.По ГОСТ 18498-73 введены обозначения различных видов червяков. Например, архимедов червяк обозначается как червяк ZA, конволютный — червяк ZN, эвольвентный -червяк ZJ и т.д. Каждый из них требует особого способа нарезания. Нарезание червяков осуществляется либо резцами на токарно-винторезных станках, либо модульными фрезами на резьбофрезерных станках.
|
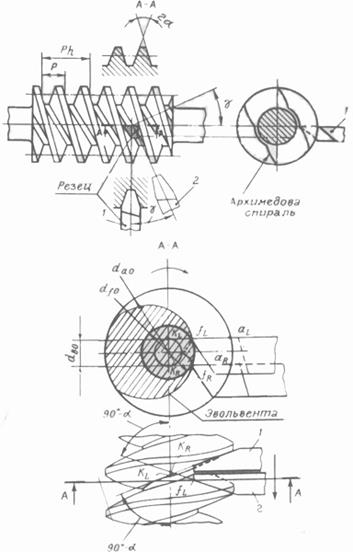 Если резец, имеющий в сечении форму трапеции, установить на токарно-винторезном станке (рис. 21.3, а) так, чтобы верхняя плоскость резца А-А проходила через ось червяка (положение 1), то при нарезании получится винтовая поверхность, которая в сечении, перпендикулярном оси червяка, дает кривую – архимедову спираль, а червяк будем называть архимедовым. Архимедов червяк в осевом сечении имеет прямолинейный профиль витка, аналогичный инструментальной рейке. Угол между боковыми
Если резец, имеющий в сечении форму трапеции, установить на токарно-винторезном станке (рис. 21.3, а) так, чтобы верхняя плоскость резца А-А проходила через ось червяка (положение 1), то при нарезании получится винтовая поверхность, которая в сечении, перпендикулярном оси червяка, дает кривую – архимедову спираль, а червяк будем называть архимедовым. Архимедов червяк в осевом сечении имеет прямолинейный профиль витка, аналогичный инструментальной рейке. Угол между боковымиповерхностями профиля витка у стандартных (по ГОСТ 19036 - 81)
червяков 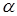 = 20°.
= 20°.
Если же резец повернуть на угол подъема винтовой линии червяка 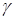 (положение 2) так, чтобы верхняя плоскость резца А-А была перпендикулярна винтовой линии, то при нарезании получится винтовая поверхность, которая в сечении, перпендикулярном оси червяка, дает кривую конволюту,а червяк соответственно будем называть конволютным.
(положение 2) так, чтобы верхняя плоскость резца А-А была перпендикулярна винтовой линии, то при нарезании получится винтовая поверхность, которая в сечении, перпендикулярном оси червяка, дает кривую конволюту,а червяк соответственно будем называть конволютным.
Для нарезания эвольвентных червяков используются два резца (рис. 21.3, б). Резец 1 с правой режущей кромкой, установленный выше оси червяка на расстоянии радиуса основного цилиндра ( 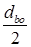 ), образует левую поверхность
), образует левую поверхность
витка. Резец 2, установленный ниже оси червяка на расстоянии радиуса основного цилиндра, образует правую поверхность витка червяка. Режущие кромки 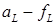 и
и 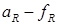 совпадают с образующими прямыми, а в результате при нарезании получается винтовая поверхность, которая в сечении, перпендикулярном оси червяка, дает кривую эвольвенту окружности.
совпадают с образующими прямыми, а в результате при нарезании получается винтовая поверхность, которая в сечении, перпендикулярном оси червяка, дает кривую эвольвенту окружности.
Червячные колеса чаще всего нарезают червячными фрезами, причем червячная фреза должна представлять собой копию червяка, с которым будет зацепляться червячное колесо. Станочное зацепление червячного колеса и фрезы воспроизводит рабочее зацепление червячной передачи. Работоспособность червячной передачи зависит от твердости и чистоты винтовой поверхности червяка, поэтому после нарезания резьбы и термообработки червяки шлифуют, а иногда и полируют.
Кинематические и геометрические соотношения в червячной передаче.Червячная передача характеризуется передаточным числом 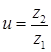 , где z2 - число зубьев колеса (обычно z2 = 18-300); z1 - число витков червяка (обычно z1 = 1 - 4), а также передаточным отношением
, где z2 - число зубьев колеса (обычно z2 = 18-300); z1 - число витков червяка (обычно z1 = 1 - 4), а также передаточным отношением 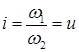 , где
, где 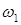 и
и 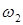 - угловые скорости соответственно червяка и колеса.
- угловые скорости соответственно червяка и колеса.
Геометрические размеры червячной передачи определяются межосевым расстоянием 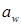 , которое зависит от диаметров червяка и колеса (рис. 21.4) и регламентируется ГОСТ 2144-76.
, которое зависит от диаметров червяка и колеса (рис. 21.4) и регламентируется ГОСТ 2144-76.
Главными параметрами червяка являются модуль т и коэффициент диаметра q. Модулем червяка называют линейную величину, в п раз меньшую расчетного шага червяка. Расчетным шагом червяка является делительный осевой шаг витков. У одновиткового червяка расчетным шагом является делительный ход витка, равный расстоянию между одноименными профилями данного витка по образующей делительного цилиндра. Коэффициент диаметра q равен отношению делительного диаметра червяка к его модулю: q = d1/m.
Модули и коэффициенты q регламентируются стандартом по ГОСТ 19672-74. Чтобы червяк не был слишком тонким, q увеличивают с уменьшением модуля.
Рис. 23.4
Окружности, определяющие размеры червяка в средней торцевой плоскости, называют средними концентрическими. Различают окружности: делительную, диаметром d1 , начальную, диаметром dw1,вершин витков – dа1, впадин - dfl принадлежащие соответственно поверхностям делительной, начальной, вершин витков и впадин. Диаметр делительного цилиндра червяка выбирают кратным осевому модулю червяка: 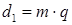
Начальный диаметр червяка без смещения равен делительному dw1 = d1. Если коэффициент смещения исходного производящего контура инструмента при нарезании червячного колеса 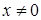 , то начальный цилиндр червяка уже не сливается с его делительным цилиндром:
, то начальный цилиндр червяка уже не сливается с его делительным цилиндром:
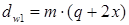
Наклон винтовой линии витка по делительному цилиндру определяют делительным углом подъема 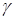 из соотношения:
из соотношения:
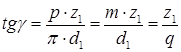
Высота головки 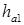 и ножки
и ножки 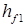 витков определяется по формулам:
витков определяется по формулам:
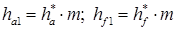
где коэффициент высоты головки 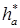 , коэффициент высоты ножки для
, коэффициент высоты ножки для
архимедовых и конволютных червяков равен 1, 2, а для эвольвентных (1 + 0,2 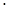 cos
cos 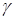 )
)
Диаметр вершин витков червяка:
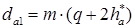
Диаметр - цилиндра впадин:
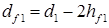
Толщина витка по делительному цилиндру:
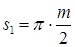
На основании ранее выведенных в лекциях 14 и 15формул для эвольвентной цилиндрической зубчатой передачи основные размеры червячного колеса в среднем сечении и червячной передачи определяют по следующим формулам:
диаметр делительной окружности:
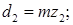
диаметр окружности вершин зубьев:
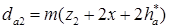
диаметр окружности впадин:
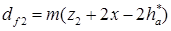
высота зуба:
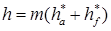
толщина зуба по делительной окружности:
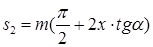
межосевое расстояние зубчатой передачи:
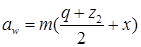
Смещение червяка в основном выполняют с целью вписывания передачи в стандартное межосевое расстояние. Коэффициент смещения х исходного производящего контура инструмента выбирают в пределах ±1. Предпочтительно использовать положительные смещения, при которых повышается прочность зубьев колеса.
Контрольные вопросы к лекции N21
1. Какие пространственные передачи относятся к гиперболоидным?
2. Чем отличаются гиперболоидная передача от червячной?
3. Какие виды винтовых передач используются в машинах? Укажите их устройства и недостатки.
4. Какие виды червячных передач используются в машинах?
5. Расскажите о способах изготовления червяков и червячных колёс?
6. Какими особенностями кинематики червячных передач вызвано скольжение зубьев?
7. Какие главные параметры характеризуют червяк? Дайте их определения
| <== предыдущая лекция | | | следующая лекция ==> |
| Волновые зубчатые передачи | | | Лекция 25. |
Дата добавления: 2015-03-14; просмотров: 2444;
