ЗУБЧАТЫЕ КОНИЧЕСКИЕ ПЕРЕДАЧИ
§ 1. БАЗОВЫЕ ЗАДАЧИ ГИДРОДИНАМИКИ ПРИ ПРОМЫВКЕ И ЦЕМЕНТИРОВАНИИ СКВАЖИН
Основные задачи гидродинамики в бурении основаны на общих уравнениях и задачах гидромеханики, в первую очередь на уравнениях состояния идеальных и реальных жидкостей, которыми чаще всего пользуются при расчетах.
При промывке и цементировании скважин простейшими типовыми задачами гидромеханики, допускающими аналитическое решение, являются задачи о течении жидкости в плоской щели (между двумя параллельными бесконечными пластинками), в круглой трубе и в кольцевом пространстве между двумя соосными цилиндрами, если исходить из следующих условий:
1) жидкость несжимаемая (ρ=соnst);
2) течение установившееся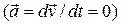 
;
3) все частицы жидкости движутся параллельно твердым стенкам канала, т. е. при совмещении координатной оси Оz с направлением течения, отличной от нуля будет лишь одна составляющая vz cкорости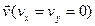 
;
4) концевые эффекты пренебрежимо малы, т. е. картина течения в любом сечении, нормальному к потоку, идентична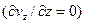 
, что справедливо для сечений, удаленных от концов канала на расстояние равное 0,035 dRe, где d – характерный размер поперечного сечения: для щели – расстояние между плоскостями; для труб – ее диаметр; для кольцевого пространства – удвоенный зазор;
5) вдоль потока действует постоянный градиент давления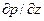 
равный – Δp/L, где Δp>0 – полный перепад давления между сечениями, находящимися на расстоянии L друг от друга;
6) на жидкость действует объемная сила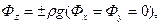 
обусловленная только силой тяжести, где принимают знак (+), если жидкость движется вниз, и знак (-) – вверх, когда положительное направление оси Оz совпадает с направлением движения.
Если, кроме того, учесть, что скорости частиц жидкости в рассматриваемых каналах симметричны относительно плоскости yz – для щели и относительно оси Оz – для круглой трубы и кольцевого пространства, то vz = v(x) и vz = v(r) соответственно.
Поэтому, согласно соотношениям Коши (15) и уравнениям состояния (14) при течении жидкости в щели, отличными от нуля будут лишь одна скорость деформации и одно напряжение сдвига:
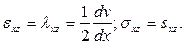(3.1)
Аналогично для течения в трубе и в кольцевом пространстве:
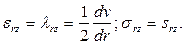(3.2)
Система дифференциальных уравнений (11) — (14) существенно упрощается: первые два уравнения движения и уравнение неразрывности удовлетворяются тождественно, а третье уравнение системы (14) принимает вид —
при течении в плоской щели
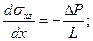
при течении в трубе и кольцевом пространстве
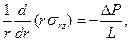
где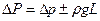 
— гидродинамические потери давления, обусловленные только движением жидкости независимо от направления течения.
Интегрируя эти уравнения при условиях σxz = 0 при х = 0 для щели и σrz = 0 при r = 0 для круглой трубы, получим соответственно
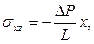(3.3)
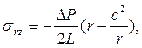(3.4)
где постоянная интегрирования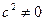 
только при течении жидкости в кольцевом пространстве.
Следует напомнить, что соотношения (3.1) — (3.4) справедливы при ламинарном течении любой (ньютоновской и неньютоновской) жидкости. Сохраняются они и при турбулентном течении, если под величинами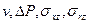 
понимать усредненные по времени значения 
.
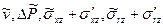Ниже приводятся аналитические решений граничных задач жидкости в щели и в кольцевом пространстве в зависимости от характера течения и реологических свойств жидкости. Решения для круглой трубы получаются простым предельным переходом из решений для кольцевого пространства.
Определяются также основные интегральные гидродинамические характеристики потока:
объемный расход
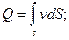
средняя скорость
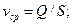(3.5)
коэффициент сопротивления
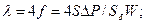
где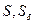 
- соответственно площади поперечного сечения и боковой смоченной поверхности канала; f = τ/W – коэффициент трения Фаннинга; 
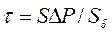- касательное напряжение у поверхности канала; 
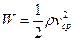- кинетическая энергия единицы объема жидкости.
Определение объемного расхода Q по заданному перепаду давления ΔР обычно называют прямой задачей гидродинамики, а определение перепада давления ΔР по заданному расходу Q – обратной задачей.
В этом отношении все приведенные ниже результаты относятся к решениям прямой граничной задачи, а полученные зависимости пользуются для вычисления гидравлических потерь. Для этой цели определяющим является закон сопротивления, т. е. зависимость коэффициента λ от характеристик течения.
Установление экспериментального закона сопротивления – задача практической гидродинамики (гидравлики), где приведенные ниже аналитические зависимости основополагающи.
Если λ не зависит от ΔР, то из третьей формулы (22) следует известный закон Дарси-Вейсбаха, широко используемый для вычисления гидравлических потерь в цилиндрических каналах при турбулентном режиме течения:
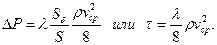
§ 2. Ламинарное и турбулентное течение жидкостей в щелевом канале
1. При ламинарном течении ньютоновской жидкости, согласно соотношениям (3.1), сохраняется только одно из уравнений состояния (2.24), а именно
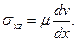(3.6)
Из сравнения этого уравнения с решением (3.3) следует дифференциальное уравнение относительно скорости
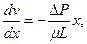
решение которого при граничном условии v(h) = 0 имеет вид
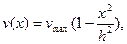(3.7)
где 2h - ширина щели.
В результате по формулам (3.5) легко определяются основные характеристики потока:
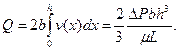
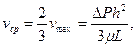(3.8)
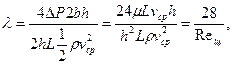
где b - длина поперечного сечения щели; Rещ = р vср2h/μ – параметр Рейнольдса для плоской щели.
2. При ламинарном течении неньютоновской жидкости Шведова –Бингама, используя соотношения (3.1) в формулах (2.26) и (2.27), получим
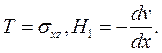(3.9)
где выбран знак (-), так как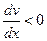 
. Поэтому система уравнений (2.24) упрощается до одного уравнения
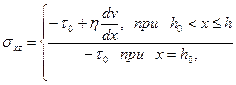(3.10)
где 2h0 – жесткое ядро потока (рис. 22).
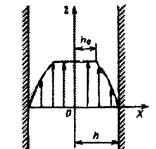
Рис. 22. Характерный вид профиля скорости в щели при течении неньютоновской жидкости Шведова – Бингама.
Из сравнения соотношений (3.3) и (3.10), получим уравнение скорости
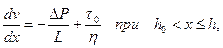(3.11)
и формулу для вычисления ядра потока
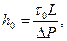(3.12)
Интегрируя уравнения (3.11) при условии v(h) = 0,найдем следующее распределение скорости:
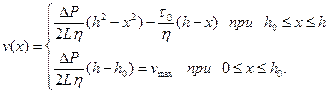(3.13)
Отсюда следует, что при h0 = h движение жидкости происходить не будет, так как v(x) = 0. Поэтому условием существования движения является h0 < h или, используя формулу (3.12),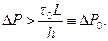 
Однако если учесть, что начало движения рассматриваемой жидкости обусловлено не динамическим напряжением сдвига τ0, а статическим τ00> τ0 , то условием страгивания покоящейся жидкости будет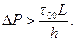 
По формулам (3.5) определяются основные характеристики потока, впервые полученные М. П. Воларовичем и А. М. Гуткиным:
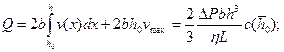(3.14)
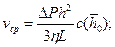
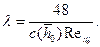
где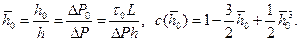 
Видно, что в данном случае кинематические характеристики потока Q, vcp и коэффициент сопротивления λ зависят от градиента давления нелинейно, что вызывает известные трудности при решении обратной задачи.
Если исходить из того, что практический интерес представляют случаи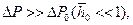 
то, приняв 
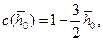получим
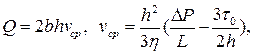
(3.15)
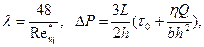
где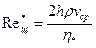 
- обобщенный параметр Рейнольдса; 
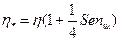приведенная вязкость жидкости Шведова-Бингама;
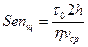- параметр Сен-Венана для плоской щели.
3. Для неньютоновской жидкости Освальда — Вейля, используя в последней системе уравнений (2.24) соотношения (3.1) и (3.9), получим
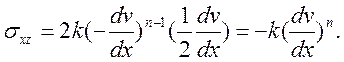
При сопоставлении этого уравнения состояния с (3.3) приходим к относительно скорости:
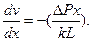(3.16)
Интегрируя это уравнение при граничном условии v(h) = 0, получим распределение скорости
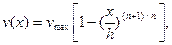(3.17)
где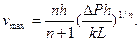 
В результате интегральные характеристики потока (3.5) будут
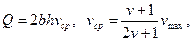
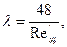(3.18)
где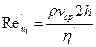 
- обобщенный параметр Рейнольдса и 
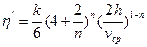— приведенная вязкость жидкости Освальда-Вейля для плоской щели. При
n =1 и k = μ формулы (3.17) — (3.18) совпадут с формулами (3.7) —(3.8).
4. При турбулентном режиме течения, когда параметры Rе, Re* или Rе' больше критических значений, решение уравнения движения записывается в виде [сравните с (3.3)]
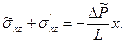(3.19)
Касательное напряжение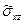 
в зависимости от типа жидкости связано со скоростью сдвига 
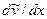уравнениями вида (3.6), (3.10) или (3.16). Напряжение Рейнольдса 
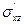в силу соотношений (2.20), (3.1) и (3.9) удовлетворяет уравнению Прандтля:
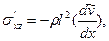(3.20)
где принимается, что величина l линейно зависит от расстояния до стенки канала s = h - x, т. е.
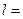
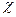s, (3.21)
где 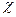— константа, определяемая из опыта.
Напряжение 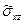имеет существенное значение лишь в непосредственной близости от стенок канала, т. е. в узкой области, состоящей из ламинарного подслоя и буферной зоны, где ламинарные и турбулентные законы течения сравнимы между собой.
В основной области течения (турбулентное ядро) можно пренебречь напряжением 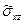. Поэтому после подстановки (3.20) и (3.21) в (3.19) получим следующее исходное дифференциальное уравнение:
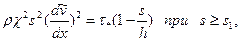(3.22)
где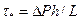 
- приведенное значение касательного напряжения; s1—внешняя граница буферной зоны.
Прандтль ввел в уравнение (3.22) упрощение (физически, вообще говоря, ничем не обоснованное), положив правую часть уравнения равной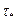 
. Но доказывается, что это упрощение вносит в конечный результат весьма небольшую погрешность.
Если, кроме того, ввести обозначение для динамической скорости на стенке канала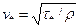 
, то уравнение (3.22) примет вид
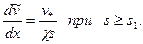
Интегрируя это уравнение при условии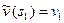 
, получим следующий универсальный закон распределения скорости:
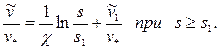(3.23)
В области, близкой к стенке канала (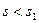 
), профиль скорости отклоняется от распределения (3.23). Однако, учитывая, что отношение 
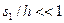, можно в гидродинамических расчетах не принимать во внимание профиль скорости в пристенной области.
Многочисленные экспериментальные исследования показали, что логарифмическое распределение (3.23) достаточно хорошо описывает профили скоростей при турбулентных течениях различных жидкостей в плоских и круглых каналах с гладкими и шероховатыми стенками вплоть до больших значений параметра Рейнольдса (за исключением, разумеется, узких пристенных областей). Различия могут составлять лишь входящие в (3.23) параметры.
Тогда для практически гладких и вполне шероховатых каналов формула (3.23) переписывается в виде
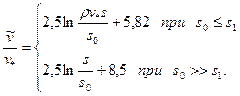(3.24)
При s = h - получим максимальные значения скоростей
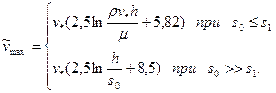(3.25)
С учетом (3.25) формулы (3.24) можно записать так:
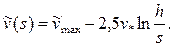(3.26)
Отсюда путем интегрирования легко получить среднюю по сечению скорость потока
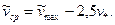(3.27)
Найдем коэффициент сопротивления по формуле (3.8):
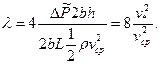
Если здесь воспользоваться формулами (3.27), (3.25) и преобразованием
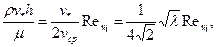
то получим универсальный закон сопротивления:
для гладкого канала:
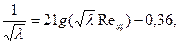(3.28)
для вполне шероховатого канала
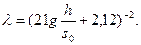(3.29)
Из формул (3.28) и (3.29) следует вывод: для гладких стенок коэффициент сопротивления λ зависит только от параметров Рейнольдса, а для вполне шероховатых — от отношения s0/h.
При переходном режиме, т. е. когда выполняется условие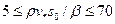 
, коэффициент сопротивления зависит от Rе и s0/h.
Способ его определения в этом случае, основанный на экспериментальных данных. В практических расчетах обычно в формулах (3.24) и (3.25) константу 8,5 заменяют на 9 и соответственно в формуле (3.29) — константу 2,12 на 2,3. Эти константы для каналов с естественной шероховатостью устанавливаются опытным путем.
Примечание. Все приведенные в этом параграфе формулы могут быть использованы и при расчете характеристик течения жидкостей по наклонной плоскости или в длинном лотке (желобе), у которого ширина b днища во много раз больше глубины потока h. Для этого необходимо принять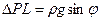 
и заменить 2b на b, где 
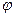— угол наклона плоскости (лотка) к горизонту.
§ 3. Ламинарное и турбулентное течение жидкостей в кольцевом канале
1. Для ньютоновской жидкости, используя соотношение (3.2) в системе уравнений (2.24), получим простейшее уравнение состояния
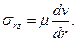
Из сравнения с решением (3.4) следует уравнение относительно скорости
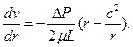
Решение этого дифференциального уравнения, удовлетворяющее граничным условиям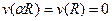 
, имеет вид
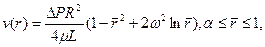(3.30)
где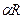 
и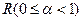 
— радиусы внутреннего и внешнего цилиндров, ограничивающих кольцевой канал; 
,
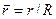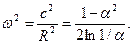(3.31)
Нетрудно убедиться в том, что максимальная скорость жидкости будет при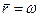 
, а интегральные характеристики потока
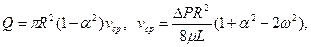
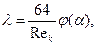(3.32)
где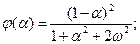 
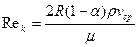— параметр Рейнольдса для кольцевого канала.
Легко проверить, что при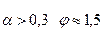 
и поэтому 
.
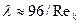Сравнивая полученные результаты с формулами (3.8), можно сделать вывод, что кольцевой цилиндрический канал с отношением радиусов окружностей сечения
α> 0,3 и плоская щель с параметрами сечения 2h = R (1 - α) и b = πR (1+ α) эквивалентны между собой в отношении интегральных гидродинамических характеристик при ламинарном течении ньютоновской жидкости, т. е. величин vcp, Q, λ, ΔР. Однако эти каналы имеют и существенное различие: переход от ламинарного режима течения к турбулентному в кольцевом канале наступает быстрее, чем в плоской щели, так как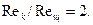 
Из формул (3.30) и (3.32) при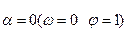 
вытекают известные формулы Хагена - Пуазейля, характеризующие течение жидкости в круглой трубе:
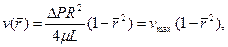
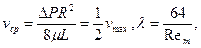
где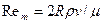 
— параметр Рейнольдса для трубы.
2. Для ньютоновской жидкости Шведова — Бингама, если учесть характер распределения скорости (3.30) в кольцевом зазоре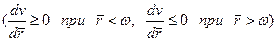 
и соотношения (3.2) в формулах (2.26) и (2.27), получим
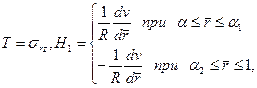
где α1R и α2R — радиусы цилиндрических поверхностей, ограничивающих жесткое ядро потока (рис. 8). Используя также соотношения (3.2), из (2.24) получим следующее уравнение состояния:
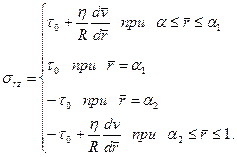
Из сопоставления с решением (3.4) имеем следующее дифференциальное уравнение относительно скорости:
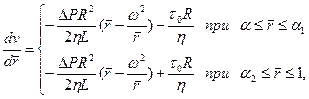(3.33)
а также уравнения относительно параметров α1 и α2 (безразмерные радиуса ядра потока) и ω = с / R:
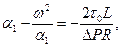
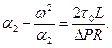(3.34)
Интегрируя уравнение (3.33) при граничных условиях v (α) = v (1) = 0, получим профиль скорости
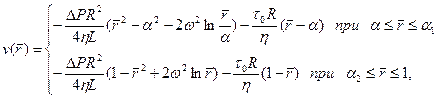(3.35)
а из уравнений (3.34) следует, что
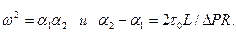(3.36)
Если в последнем соотношении (3.36) принять α1 = α и α2 = 1, то получим условие отсутствия движения
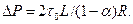
Следовательно, течение неньютоновской жидкости Шведова — Бингама в кольцевом канале возможно при условии
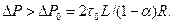
Из условия сопряжения скорости при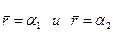 
вытекает третье уравнение относительно искомых параметров
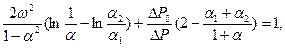(3.37)
которое с помощью соотношений (3.36) сводится к трансцендентному уравнению относительно одного из параметров ω2, α1 или α2, допускающему лишь численное решение.
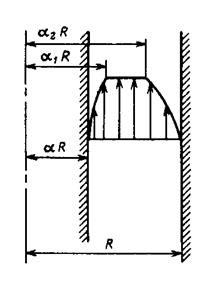
Рис. 23. Характерный вид профиля скорости в кольцевом канале при течении ньютоновской жидкости Шведова-Бингама.
В табл. 1 приведены значения параметров α1, α2 и ω, полученные путем численного решения уравнений (3.36) и (3.37) на ЭВМ с точностью до 1%.
Таблица 1
| ΔP0/ΔP | α | |||||||||||
| 0,45 | 0,55 | 0,65 | 0,75 | |||||||||
| α1 | α2 | ω | α1 | α2 | ω | α1 | α2 | ω | α1 | α2 | ω | |
| 0,1 | 0,68 | 0,74 | 0,71 | 0,74 | 0,79 | 0,76 | 0,8 | 0,84 | 0,82 | 0,86 | 0,89 | 0,87 |
| 0,3 | 0,63 | 0,79 | 0,7 | 0,7 | 0,83 | 0,76 | 0,77 | 0,87 | 0,82 | 0,84 | 0,91 | 0,87 |
| 0,5 | 0,57 | 0,85 | 0,69 | 0,65 | 0,88 | 0,76 | 0,73 | 0,91 | 0,81 | 0,81 | 0,94 | 0,87 |
| 0,7 | 0,52 | 0,91 | 0,69 | 0,61 | 0,93 | 0,75 | 0,7 | 0,94 | 0,81 | 0,79 | 0,96 | 0,87 |
| 0,9 | 0,48 | 0,97 | 0,68 | 0,57 | 0,98 | 0,75 | 0,67 | 0,98 | 0,81 | 0,77 | 0,99 | 0,87 |
Видно, что параметр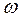 
очень слабо зависит от отношения 
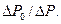Максимальное различие между значениями ω при 
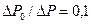и 0,9 составляет: 3,5% — при α = 0,45; 2%— при α = 0,55; 1% — при α = 0,65. Следовательно, параметр ω можно с высокой точностью вычислить по той же формуле, что и в задаче течения ньютоновской жидкости (3.31), т. е.
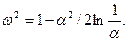
Решая систему уравнений (3.36), найдем с точностью до первого порядка относительно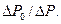
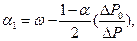
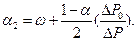
Из сравнения с табличными значениями α1 и α2 легко убедиться, что погрешность такого приближения не более 4% для α1, и 2% для α2.
После подстановки полученных таким образом соотношений для параметров α1, α2 и ω в (3.35), интегрирования по кольцевому сечению и пренебрежения слагаемыми, содержащими величину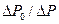 
в 3-й и 4-й степенях, получим следующий результат:
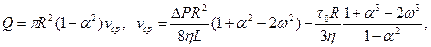(3.38)
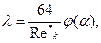или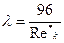 
при α > 0,3,
где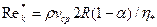 
— обобщенный параметр Рейнольдса: 
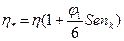— приведенная вязкость жидкости Шведова - Бингама и 
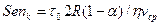- параметр Сен-Венана для кольцевого канала: 
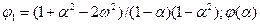- то же, что в (3.32).
Надо подчеркнуть, что приближенное решение (3.38) практически не отличается от точного при выполнении условия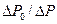 
<0,5 или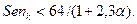 
Расчеты показывают, что параметр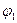 
, является практически постоянной величиной, диапазон его изменения составляет от 0,87 до 0,88 при 0,1< α <0,9.
Сравнивая формулы (3.15) и (3.38), можно сделать полезный вывод: при течении жидкости Шведова — Бингама имеет место гидравлическая эквивалентность кольцевого цилиндрического канала и плоской щели, если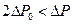 
; α >0,3; 2h = R(1- α ); b = πR(1+ α )и 
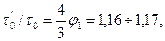где 
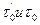- соответственно предельные напряжения сдвига для жидкостей в щелевом и кольцевом каналах. Легко заметить, что последнее требование опускается, если принять 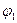=3/4, т.е. 
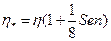. Аналогично первой задаче и здесь отношение параметров Рейнольдса Rе к* и Rещ равно 2.
В предельном случае, когда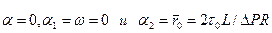 
— приведенный радиус жесткого ядра, из решений (3.35) и (3.38) следуют основные расчетные формулы для течения неньютоновской жидкости Шведова — Бингама в круглой трубе радиуса R:
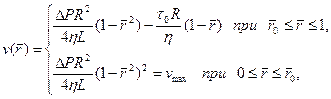(3.39)
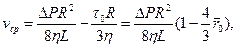(3.40)
, 
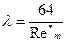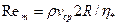— обобщенный параметр Рейнольдса, 
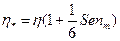— приведенная вязкость жидкости Шведова - Бингама и 
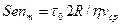— параметр Сен-Венана для трубы. Эти формулы известны как упрощенные формулы Букингама.
3. Для неньютоновской жидкости Освальда — Вейля, используя в последнем уравнении состояния (2.24) соотношения (3.2) и значение интенсивности скорости деформации сдвига [см. формулу (2.27)].
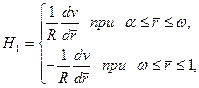
получим
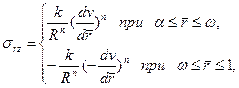(3.41)
где использованы те же обозначения, что и в предыдущих задачах.
Из сопоставления (3.41) и (3.4) приходим к дифференциальному уравнению
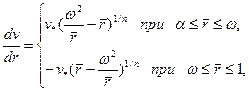
где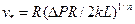 
— некоторая характерная величина скорости.
Интегрируя последнее уравнение при граничных условиях v (α) = v (1) = 0, получим профиль скорости
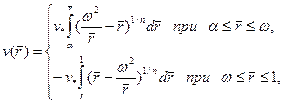(3.42)
Из условия сопряжения скорости при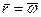 
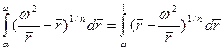(3.43)
определяется параметр ω.
В общем случае (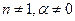 
) интегралы в формуле (3.42) и в уравнении (3.43) нельзя представить элементарными функциями, и поэтому вычисления следует выполнять с помощью численного интегрирования на ПК. То же относится и к вычислению средней скорости потока
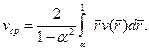(3.44)
Численное решение уравнения (3.43) показывает, что параметр ω (безразмерная координата максимальной скорости) практически не зависит от реологической константы модели п и весьма точно может быть вычислен по формуле (3.31). Это иллюстрирует рис. 24, где показаны профили скорости для нескольких значений п, построенные по формулам (3.42) и (3.43) при α = 0,6.
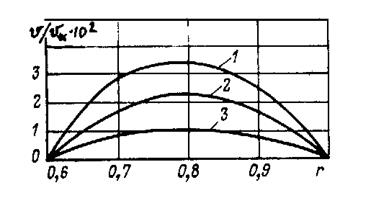
Рис. 24. Профили скорости при α = 0,6 для степенной модели Освальда — Вейля:
1, 2, 3 - соответственно при n = 0,9; 0,7; 0,5.
С достаточной точностью рассчитать среднюю скорость можно по формуле
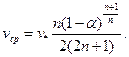(3.45)
При этом коэффициент гидравлического сопротивления
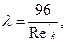
где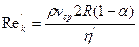 
- обобщенный параметр Рейнольдса, 
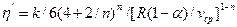— приведенная вязкость жидкости Освальда — Вейля для кольцевого канала. В предельном случае, когда 
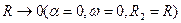, уравнение (3.43) не имеет смысла, а из зависимости (3.42) следует элементарная формула для распределения скорости в сечении круглой трубы
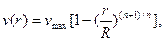
где
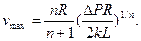
Поэтому основные интегральные характеристики потока жидкости в трубе принимают вид
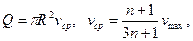
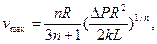
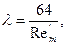
где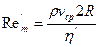 
— обобщенный параметр Рейнольдса и 
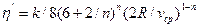— приведенная вязкость жидкости для трубы.
4. При турбулентном режиме течения, учитывая соотношения (3.1) и характер распределения профиля скорости [см., например, соотношение (3.41)], найдем по уравнениям Прандтля (2.20) связь напряжения Рейнольдса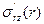 
с усредненной по времени скоростью 
:
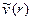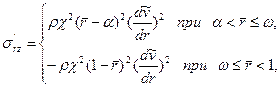(3.46)
Если исходить из тех же упрощающих предположений Прандтля, что и в области основного турбулентного ядра напряжения 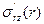, принять равными касательным напряжениям на стенках канала соответственно слева и справа от цилиндрической поверхности r = ωR, то, используя формулу (21) при r = αR и r = R, получим
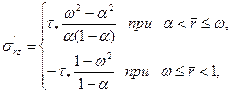(3.47)
где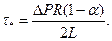 
Из сравнения соотношений (3.46) и (3.47) получим уравнение относительно скорости
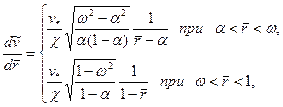
где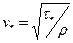 
- характерная скорость. Интегрируя данное уравнение с учетом условия 
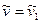при 
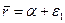и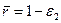 
, получим закон распределения скорости в кольцевом канале
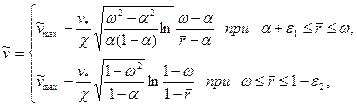(3.48)
где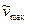 
— максимальная скорость потока:
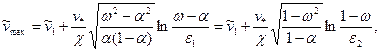(3.49)
содержит экспериментальные параметры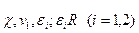 
— размеры пристенных слоев у внутренней и внешней стенок канала.
Из равенства (3.49) следует уравнение относительно параметра ω
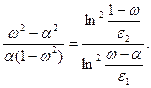(3.50)
Для упрощения решения этого трансцендентного уравнения примем, что отношения размеров зон турбулентного ядра и пристенных слоев слева и справа от поверхности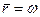 
равны между собой, т. е.
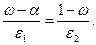(3.51)
Тогда из уравнения (3.50) получим
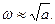(3.52)
Путем интегрирования профиля скорости (3.48), пренебрегая пристенными слоями и используя равенство (3.52), легко найти среднюю скорость турбулентного потока
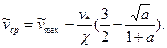(3.53)
Согласно формуле (3.5) коэффициент сопротивления
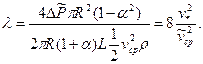
Отсюда, учитывая формулы (3.49), (3.52) и (3.53), получим
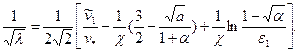
Принимая по аналогии с задачей для гладких стенок: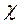 
= 0,4; 
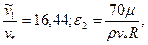закон сопротивления для кольцевого канала запишем в виде
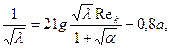(3.54)
где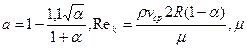 
- вязкость или приведенная вязкость жидкости.
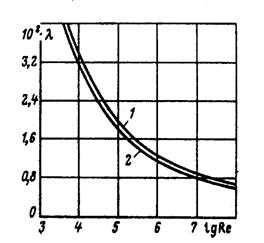
Рис. 25. Зависимость коэффициента сопротивления от параметра Рейнольдса (закон сопротивления) при турбулентном режиме течения:
1, 2 – соответственно при α = 0,9 и α = 0.
Если α = 0, то а=1 и соотношение (3.54) выражает известный универсальный закон сопротивления Прандтля для гладких труб, который неоднократно был проверен опытами.
При α > 0,3 величина а изменяется в пределах от 0,54 до 0,45. Следовательно, для малых кольцевых зазоров (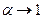 
) закон сопротивления (3.54) принимает вид закона сопротивления для щели (3.28), где 2h = R( 1 - α).
Из рис. 25 следует вывод, что закон сопротивления при турбулентном режиме течения слабо зависит от α, т. е. от формы канала (круглая труба, кольцевое пространство или щель). В диапазоне чисел Рейнольдса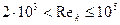 
кривые на рис. 25 можно аппроксимировать функцией 
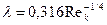, которую принято называть формулой Блазиуса.
Таблица 2.
| S0/R | а | ||||
| 0,3 | 0,5 | 0.7 | 0,9 | ||
| 0,001 | 0,016 | 0,018 | 0,02 | 0,023 | 0,032 |
| 0,005 | 0,025 | 0,027 | 0,031 | 0,037 | 0,056 |
| 0,01 | 0,03 | 0,034 | 0,038 | 0,047 | 0,077 |
| 0,025 | 0,041 | 0,046 | 0,054 | 0,069 | — |
| 0,05 | 0,053 | 0,062 | 0,073 | — |
Отсюда непосредственно находят коэффициент сопротивления по высоте элемента шероховатости s0 стенки канала. Некоторые значения λ, вычисленные по этой формуле, приведены в табл. 2.
Полученные выше решения дают основание сделать следующий практический вывод: при гидравлических расчетах или обработке опытных данных кольцевой канал скважины можно рассматривать как щель с параметрами 2h = R( 1 - α) и b =π R( 1 + α). При этом точность расчета будет зависеть в основном от точности значений реологических параметров жидкости и геометрических параметров кольцевого зазора.
Для расчета гидравлических потерь при турбулентном режиме течения жидкости в затрубном пространстве открытой части ствола скважины необходимо воспользоваться формулой Дарси — Вейсбаха, в которой среднестатистическое значение коэффициента λ должно быть установлено по опытным данным в п типовых скважинах.
ЗУБЧАТЫЕ КОНИЧЕСКИЕ ПЕРЕДАЧИ
Дата добавления: 2015-02-19; просмотров: 1200;