Волновые зубчатые передачи

Рассмотрим один из методов, используемых при подборе чисел зубьев планетарного редуктора, - метод сомножителей. Метод позволяет объединить в расчетные формулы некоторые из условий подбора (условия 1, 2, 5 и 6). Выполнение остальных условий для выбранных чисел зубьев проверяется. Из первого условия выразим внутреннее передаточное отношение механизма. Внутренним называют передаточное отношение механизма при остановленном водиле, то есть механизма с неподвижными осями или рядного механизма.

u₁₄ ^h = (z₂ * z₄)/(z₁ * z₃) = [ u_1h / ( 0.95 … 1.05 ) – 1] = (B * D)/(A * C).

Разложим внутреннее передаточное отношение u₁₄^h на сомножители - некоторые целые числа A, B, Cи D.При этом сомножитель Aсоответствует числу зубьев z₁ , B - z₂ , C - z₃ и D - z₄.Сомножители могут быть произвольными целыми числами, комбинация (B D) / (A C)которых равна u₁₄^h.

Для рассматриваемой схемы желательно придерживаться следующих диапазонов изменения отношений между сомножителями:

B / A = z₂ / z₁ = 1 … 6-внешнее зацепление,

D / C = z₄ / z₃ = 1.1 … 8–внутреннее зацепление.

Включим в рассмотрение условие соосности:

z₁ + z₂ = z₄ - z₃

и выразим его через сомножители:

a ( A + B) = b ( D – C ).

Если принять, что коэффициенты a и b равны:

a = ( D – C ), b = (A + B),

то выражение превращается в тождество.

Из этого тождества можно записать:

z₁= ( D – C ) A q

z₃= ( A + B ) C q

z₂= ( D – C ) B q

z₄= ( A + B ) D q

где q - произвольный множитель, выбором которого обеспечиваем выполнение условий 5 и 6.

Зубья колес планетарного механизма, рассчитанные по этим формулам, удовлетворяют условиям 1, 2, 5 и 6. Проверяем эти зубья по условиям 3 (соседства) и 4 (сборки) и если они выполняются, считаем этот вариант одним из возможных решений. Если после перебора рассматриваемых сочетаний сомножителей получим несколько возможных решений, то проводим их сравнение по условию 7. Решением задачи будет сочетание чисел зубьев, обеспечивающее минимальный габаритный размер R.

Примеры подбора чисел зубьев для типовых планетарных механизмов.

1. Двухрядный планетарный редуктор с одним внешним и с одним внутренним зацеплением.

Дано: Схема планетарного механизма, u_1h = 13, k = 3.

Определить: z_i

Внутреннее передаточное отношение механизма:

u₁₄ ^h = (z₂ z₄) / (z₁ z₃) = [ u_1h / ( 0.95 … 1.05 ) – 1] = 12 = (B D)/(A C) = 3 4 / (1 1) = 2 6 / (1 1)= 4 3 / (1 1) = ...

Для первого сочетания сомножителей:

z₁= ( D – C ) A q = ( 4 – 1 ) 1 q = 3 q ; z₁= 18 > 17;
z₂= ( D – C ) B q = ( 4 – 1 ) 3 q = 9 q ; q = 6; z₂= 54 > 17;
z₃= ( A + B ) C q = ( 3 + 1 ) 1 q = 4 q; z₃= 24 > 20;
z₄= ( A + B ) D q = ( 3 + 1 ) 4 q = 16 q; z₄= 96 > 85;

Проверка условия соседства:

sin ( 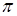/ k ) > max [( z_2,3 + 2)/ (z₁ + z₂) ]

sin ( 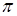/ 3 ) > (54 + 2)/(18+54)

0.866 > 0.77 -условие выполняется.

Проверка условия сборки:

( u_1h z₁ / k ) ( 1 + k p) = B;

(13 18/3) ( 1 + 3 р) = В-целое при любом p.

Условие сборки тоже выполняется. То есть, получен первый вариант решения!
Габаритный размер R = (18 + 2 Ч 54) = 126.

Для второго сочетания сомножителей:

z₁= ( D – C ) A q = ( 6 – 1 ) 1 q = 5 q ; z₁= 45 > 17;
z₂= ( D – C ) B q = ( 6 – 1 ) 2 q = 10 q ; q = 9; z₂= 90 > 17;
z₃= ( A + B ) C q = ( 2 + 1 ) 1 q = 3 q; z₃= 27 > 20;
z₄= ( A + B ) D q = ( 2 + 1 ) 6 8 q = 18 q; z₄= 162 > 85;

Проверка условия соседства:

sin ( 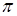/ k ) > max [( z_2,3 + 2)/ (z₁ + z₂) ]

sin ( 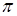/ 3 ) > (90 + 2)/(45+90)

0.866 > 0.681-условие выполняется.

Проверка условия сборки:

( u_1h z₁ / k ) ( 1 + k р) = B

(12 45 / 3) ( 1 + 3 р) = В -целое при любомр.

Условие сборки тоже выполняется и получен второй вариант решения!
Габаритный размерR = (45 + 2 90) = 225.

Для третьего сочетания сомножителей:

z₁= ( D – C ) A q = ( 3 – 1 ) 1 q = 2 q ; z₁= 18 > 17;
z₂= ( D – C ) B q = ( 3 – 1 ) 4 q = 8 q ; q = 9; z₂= 72 > 17;
z₃= ( A + B ) C q = ( 1 + 4 ) 1 q = 5 q; z₃= 45 > 20;
z₄= ( A + B ) D q = ( 1 + 4 ) 3 q = 15 q; z₄= 135 > 85;

Проверка условия соседства:

sin ( 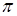/ k ) > max [( z_2,3 + 2)/ (z₁ + z₂) ]

sin ( 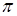/ 3 ) > (70 + 2)/(18+72)

0.866 > 0.8-условие выполняется.

Проверка условия сборки:

( u_1h z₁ / k ) ( 1 + k р) = B; (13 18/3) ( 1 + 3 р) = В-целое при любом р.

Условие сборки тоже выполняется и получен третий вариант решения.
Габаритный размерR = (18 + 2 72) = 162.

Из рассмотренных трех вариантов наименьший габаритный размер получен в первом. Этот вариант и будет решением нашей задачи.

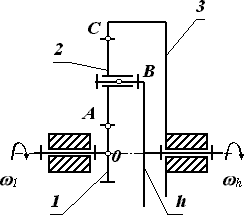2.Однорядный механизм с одним внутренним и одним внешним зацеплением.
Дано:

схема планетарного механизма, u_1h = 7; k = 3.

Определить: z_i = ?.

Для однорядного планетарного механизма задача подбора чисел зубьев решается без применения метода сомножителей. Задаемся для первого колеса числом зубьев больше 17 и кратным u_1h или k.

В нашем примере принимаем:

z₁ = 18 > 17.

Тогда из формулы передаточного отношения можно определить число зубьев третьего колеса:

u_1h = ( 1 + z₃ / z₁ ) (0.95 … 1.05)

z₃ = [u_1h / (0.95…1.05) - 1] z₁

z₃ = [ 7 / (0.95…1.05) - 1] 18 = 108

Число зубьев второго колеса определим из условия соосности:
z₁ + z₂ = z₃ - z₂

z₂ = ( z₃ - z₁ ) / 2 = ( 108 - 18 ) / 2 = 45

Проверка условия соседства:

sin ( 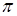/ k ) > max [( z₂ + 2)/ (z₁ + z₂) ]

sin ( 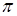/ 3 ) > (45 + 2)/(18+45)

0.866 > 0.73-условие выполняется.

Проверка условия сборки:

( u_1h z₁ / k ) ( 1 + k р) = B

(7 18/3) ( 1 + 3 р) = Вцелое при любомр.

В данном случае нет необходимости сравнивать варианты по габаритам, так как мы приняли минимально допустимую величину z₁, то получим редуктор минимальных размеров.

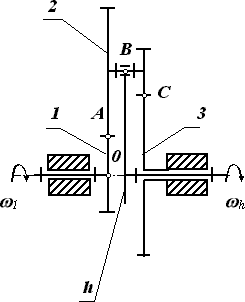
3.Двухрядный механизм с двумя внешними зацеплениями. (рис. 18.3)

Дано: схема планетарного механизма, u_h1 = -24; k =3.

Определить: z_i - ?.

u_1h= 1 / u_h1
u₁₄ ^h = (z₂ z₄)/(z₁ z₃) = [ 1 - u_1h / ( 0.95 … 1.05 ) ] = 25/24 = (B D)/(A C) = 5

5 / (4 6) = 5 5 / (6 4)= 25 1 / (12 2) = ...

Условие соосности для этой схемы:

z₁ + z₂ = z₄ + z₃

и выразим его через сомножители:

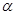
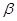
( A + B) = ( D + C ).

Принимаем коэффициенты 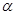и :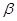

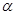= ( D + C ), 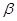= (A + B).

и получаемдля сочетания сомножителей обведенного рамкой:

z₁= ( D + C ) A q = ( 1 + 2 ) 12 q = 36 q ; z₁= 36 > 17;
z₂= ( D + C ) B q = ( 1 + 2 ) 25 q = 75 q ; q = 1; z₂= 75 > 17;
z₃= ( A + B ) C q = ( 12 + 25 ) 2 q = 74 q; z₃= 74 > 17;
z₄= ( A + B ) D q = ( 12 + 25 ) 1 q = 37 q; z₄= 37 > 17;

Проверка условия соседства:

sin ( 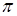/ k ) > max [( z_2,3 + 2)/ (z₁ + z₂) ];

sin ( 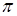/ 3 ) > (75 + 2)/(36+75)

0.866 > 0.694 -условие выполняется.

Проверка условия сборки:

( u_1h z₁ / k ) ( 1 + k р) = B;

[18 / (-24 3)] ( 1 + 3 р) = В -целое при р=1.

Условие сборки тоже выполняется. То есть, получен первый вариант решения.

Габаритный размерR = (36 + 2 75) = 186.

Аналогичным образом рассматриваются другие сочетания сомножителей и из вариантов, удовлетворяющих первым шести условиям, выбирается тот, который обеспечивает наименьшие габариты.

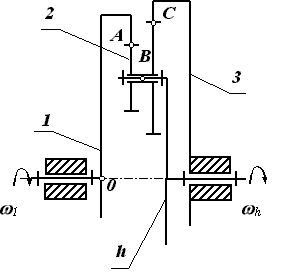4.Двухрядный механизм с двумя внутренними зацеплениями.
Дано:

схема планетарного механизма (рис. 18.4), u_1h = 55; k = 2.

Определить: z_i =?.

Внутреннее передаточное отношение механизма:

u_1h= 1 / u_h1;

u₁₄ ^h = (z₂ z₄)/(z₁ z₃) = [ 1 - u_1h / ( 0.95 … 1.05 ) ] = 54 / 55 = (B D)/(A C) = 6 9 / (11 5) = 18 3 / (55 * 1) = ...

Условие соосности для этой схемы:

z₁ - z₂ = z₄ - z₃

и выразим его через сомножители:

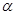
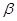
( A - B) = ( D - C )

Принимаем коэффициенты 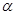и из условия тождественности :

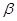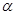= ( D - C ), 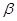= (A - B)

и получаемдля сочетания сомножителей обведенного рамкой:

z₁= ( D - C ) A q = ( 3 - 1 ) 55 q = 110 q ; z₁= 110 > 85;
z₂= ( D - C ) B q = ( 3 - 1 ) 18 q = 36 q ; q = 1; z₂= 36 > 20;
z₃= ( A - B ) C q = ( 55 - 18 ) 1 q = 37 q; z₃= 37 > 20;
z₄= ( A - B ) D q = ( 55 - 18 ) 3 q = 111 q; z₄= 111 > 85;

Проверка условия соседства:

sin ( 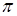/k ) > max [( z_2,3 + 2)/ (z₁ + z₂) ]

sin ( 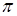/2 ) > (37 + 2)/(110 - 36)

1.0 > 0.527 -условие выполняется.

Проверка условия сборки:

( u_1h z₁ / k ) ( 1 + k р) = B;

[110 / (55 2)] ( 1 + 3 р) = В-целое при любомр.

Условие сборки тоже выполняется. То есть, получен первый вариант решения.
Аналогичным образом рассматриваются другие сочетания сомножителей и из вариантов, удовлетворяющих первым шести условиям, выбирается тот, который обеспечивает наименьшие габариты.

Оптимальный синтез планетарных механизмов при автоматизированном проектировании.

При автоматизированном проектировании с помощью компьютера можно за относительно небольшой промежуток времени получить большое количество возможных решений задачи. Сопоставляя эти решения между собой находят то, которое удовлетворяет всем требованиям наилучшим образом. При этом перебор вариантов осуществляется в пределах заданных ограничений на параметры (в данном случае на числа зубьев колес) по какой-либо стратегии или чаще случайным образом. Программы оптимального синтеза могут использовать рассмотренные выше методы (например, метод сомножителей), а могут просто перебирать допустимые сочетания параметров и проверять их на соответствие заданным условиям. Использование компьютерных программ для синтеза планетарных механизмов позволяет существенно сократить время проектирования и существенно улучшить качественные показатели спроектированных механизмов.

Планетарные дифференциальные механизмы с W=2.

На практике в качестве механизмов с двумя подвижностями наиболее часто применяются планетарные зубчатые механизмы или как их еще называют планетарные дифференциалы. Это название справедливо для механизмов, в которых входной энергетический поток разделяется на два выходных потока. Если входные энергетические потоки суммируются на выходе в один выходной поток, то такие механизмы следует называть суммирующими или интегральными.

Все рассмотренные типовые схемы механизмов можно выполнить с двумя подвижностями. Рассмотрим в качестве примера двухрядный механизм с одним внешним и одним внутренним зацеплением (рис.18.5).

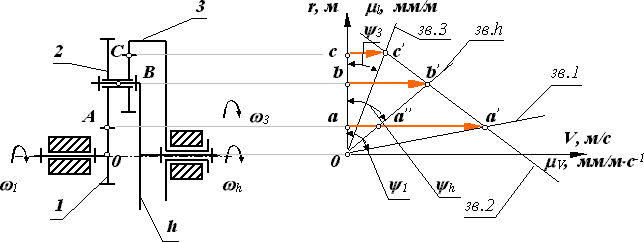
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z₂иz₁

( ₁ - _h) / ( ₂ - _h) = - z₂ / z₁

для внутреннего зацепления колес z₄иz₃

( ₂ - _h) / ( ₃ - _h) = z₄ / z₃ .

Перемножим, правые и левые части этих уравнений, и получим соотношение между угловыми скоростями механизма с двумя подвижностями

[( ₁ - _h) / ( ₂ - w_h)] [( ₂- _h)/ ( ₃- _h)] = - z₂ z₄ / ( z₁ z₃)

( ₁ - _h) / ( ₃ - _h) = - z₂ z₄ / ( z₁ z₃) = u₁₃^(h)

u₁₃ ^(h) ₃ - u₁₃ ^(h) _h = ₁ - _h

1 - ( 1 + u13 (h)) h - u13 (h) 3 = 0

Чтобы из механизма с двумя подвижностями получить одноподвижный механизм необходимо либо остановить одно из подвижных звеньев, либо связать между собой функционально ( например, простой зубчатой передачей ) два подвижных звена. Механизмы, образованные по второму способу, называются замкнутыми дифференциалами. Схема такого замкнутого дифференциального механизма приведена на рис.18.6.

Контрольные вопросы к лекции N18.

1. Как формулируется задача кинематического синтеза планетарного механизма?

2. Какие основные условия необходимо выполнить при синтезе многосателитного планетарного механизма? Перечислите их.

3. Запишите условие соседства для однорядного планетарного механизма с K=3 ?

4. Как обеспечивается условие сборки многосателитного планетарного механизма?

5. Как определяются числа зубьев (любой из схем) планетарного механизма методом сомножителей?

6. Определите числа зубьев однорядного планетарного механизма с 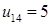и К=3.

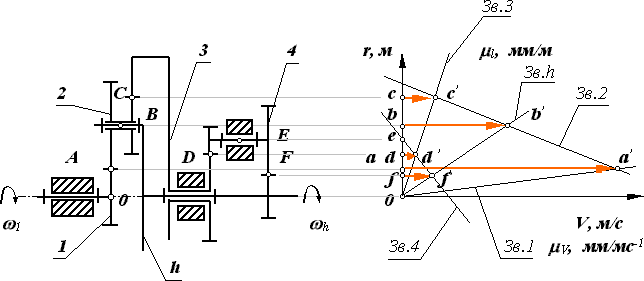
7. Как устанавливаются кинематические зависимости в дифференциальном планетарном механизме графическим способом?

Волновые зубчатые передачи

Волновая зубчатая передача — механизм, содержащий зацепляющиеся между собой гибкое и жесткое зубчатые колеса и обеспечивающий преобразование и передачу движения благодаря деформированию гибкого колеса (рис. 19.1).

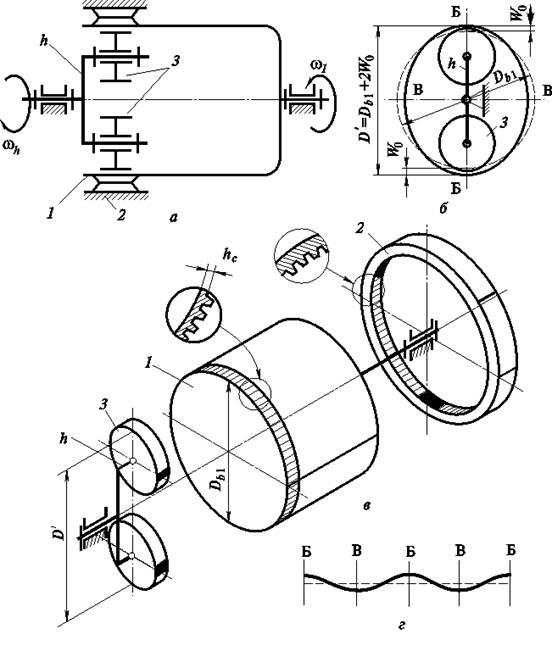
Рис. 19.1

Волновая зубчатая передача (ВЗП) состоит из трех основных элементов: гибкого колеса 1 (рис. 19.1, а, б, в), жесткого колеса 2 и генератора волн h. Ее можно рассматривать как конструктивную разновидность планетарной передачи с внутренним зацеплением, характерной особенностью которой является использование сателлита (гибкого колеса), деформируемого в процессе передачи движения. Гибкое зубчатое колесо представляет собой тонкостенную оболочку, один конец которой соединен с валом и сохраняет цилиндрическую форму, а на другом нарезан зубчатый венец с числом зубьев 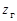. При сборке этот конец оболочки деформируется на 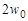генератором волн. Контур деформированного гибкого колеса образует относительно недеформированного две волны деформации (рис. 19.1, г). Размер по сечению Б – Б называют большой осью, а по В – В — малой осью кривой деформации. В зоне большой оси деформации происходит зацепление зубьев гибкого и жесткого колес. Для обеспечения симметрии нагружения волновой зубчатой передачи обычно используют две волны деформации и четные числа зубьев колес, которые связаны соотношением .

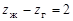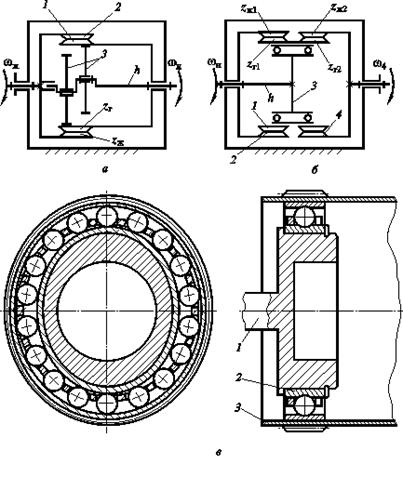
Рис. 19.2

Гибкое колесо 1 поджато к жесткому 2 роликами 3, расположенными на водиле h. Такой генератор называют роликовым. Роликовый генератор волн может быть преобразован в дисковый генератор волн при значительном увеличении диаметров роликов 3 (рис. 19.2, а) и расположении их в параллельных плоскостях. Чтобы задать зубчатому венцу гибкого колеса определенную принудительную форму деформации, генератор нужно выполнить в виде симметричного кулачка специального профиля. Такой генератор называют кулачковым (рис. 19.2, в). На кулачок 1 напрессовывают гибкий подшипник 2, чтобы уменьшить трение между гибким колесом 3 и генератором волн. Дисковые и кулачковые генераторы волн применяют в высоко нагруженных передачах. Кроме механических генераторов волн применяют также электромагнитные, пневматические и гидравлические генераторы.

Кинематика волновой передачи. При вращении генератора волн обе волны деформации перемещаются по периметру гибкого колеса. В результате каждый зуб гибкого колеса за один оборот генератора волн дважды входит в зацепление с зубьями жесткого колеса. Если числа зубьев колес равны 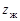и 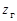, а угловые шаг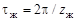и и 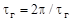, то передаточное отношение такой передачи можно подсчитать следующим образом. При остановленном жестком колесе после полного оборота генератора волн 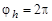вал гибкого колеса повернется в противоположном движению генератора направлении на угол, равный .

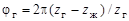Переходя от углов поворота к угловым скоростям, получаем передаточное отношение ВЗП от генератора волн к гибкому колесу при неподвижном жестком:

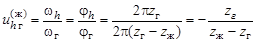. (19.1)

В ВЗП с остановленным гибким колесом при повороте генератора волн на угол 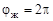жесткое колесо повернется в том же направлении на угол 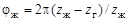. В этом случае передаточное отношение от генератора волн к жесткому колесу при неподвижном гибком

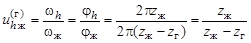. (19.2)

Волновая передача может быть двухступенчатой (рис. 19.2, б). В этом случае гибкое колесо 1 выполняется в виде кольца с двумя зубчатыми венцам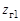и и 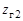, которые входят в зацепление с жесткими колесами 2 и 4, имеющими соответственно 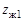и 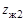зубьев. Если жесткое колесо 2 неподвижно, то движение от вала генератора волн преобразуется с помощью двух волновых зацеплений и передается на выходной вал, соединенный с жестким колесом 4. Передаточное отношение двухступенчатой ВЗП определяется формулой

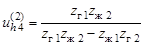. (19.3)

Особенности волнового зацепления. Гибкое колесо ВЗП при его нагружении изменяет свою начальную форму. Это происходит из-за наличия зазоров и упругости элементов, взаимодействующих с гибким колесом. Изменение формы гибкого колеса 1 ограничено с внешней стороны жестким колесом 2, а с внутренней генератором волн h. Гибкое колесо, опирающееся на генератор волн в пределах участков постоянной кривизны 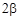(рис. 19.3), стремится принять форму жесткого колеса. С увеличением момента закручивающего гибкое колесо зоны выбранных зазоров в зацеплении увеличиваются, что приводит к увеличению числа пар зубьев в зацеплении. Благодаря многопарности зацепления (нагрузку могут передавать до 40 % всех пар зубьев) нагрузочная способность ВЗП выше, чем планетарной. КПД волновой передачи также выше, потому что в зацеплении зубья почти не перемещаются при прилегании гибкого колеса к жесткому. При стальных гибких колесах в одноступенчатых волновых передачах можно получить передаточное отношение 60 – 320, а КПД равным 0,85...0,80. Двухступенчатые ВЗП обеспечивают передаточные отношения от 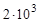до 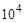и более при КПД от 0,7 до 0,1.

Многопарность и многозонность волнового зацепления приводят к значительному усреднению ошибок изготовления и сборки, в результате чего обеспечивается высокая кинематическая точность ВЗП.

Относительно небольшая величина радиальной деформации гибкого колеса позволяет выполнить его в виде колоколообразной оболочки и изготовить герметичные ВЗП, передающие вращение через герметичную перегородку без подвижных уплотнений.

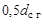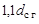Наиболее ответственные детали ВЗП — гибкий подшипник и гибкое колесо. Гибкое колесо имеет тонкостенное донышко, допускающее осевые перемещения торца цилиндрической оболочки при ее деформировании с другого края. Длину гибкого колеса выбирают от до , где 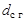— диаметр недеформированной серединной поверхности гибкого колеса. Толщину 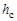гибкого колеса под зубчатым венцом выбирают примерно равной .

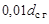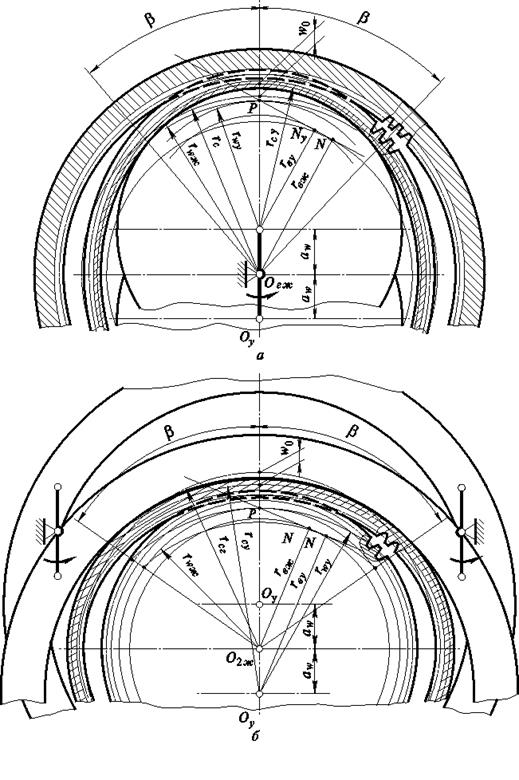
Методика проектирования ВЗП. Существует несколько методов расчета геометрических параметров волновых зубчатых передач. Настоящая методика, разработанная на кафедре теории механизмов и машин МГТУ им. Н.Э. Баумана, основывается на предположении, что конструкции генераторов волн рассматриваемых передач обеспечивают постоянную кривизну серединного слоя деформированного гибкого колеса в пределах зон зацепления, ограниченных центральными углами 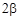(см. рис. 19.3, а). Вне этих зон гибкое колесо имеет свободную форму деформации. На участке постоянной кривизны зацепление в волновой передаче рассматривается как внутреннее эвольвентное зацепление жесткого колеса с числом зубьев 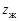и условного, имеющего параметры гибкого и расчетное число зубьев .

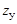Исходными параметрами для расчета являются передаточное отношение передачи, ее схема, номинальный крутящий момент на выходном валу, частота вращения генератора волн, срок службы передачи, прочностные характеристики гибкого колеса. Проектировочный расчет заключается в определении диаметра серединной поверхности гибкого колеса по изгибной прочности, из расчета на выносливость или из расчета заданного коэффициента крутильной жесткости [16]. Больший из вычисленных диаметров берется за основу для определения модуля зацепления 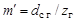, который округляется до ближайшего стандартного значения.

Делительные диаметры колес и толщина 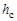обода гибкого колеса под зубчатым венцом определяются по формулам

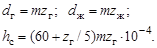(19.4)

Основным варьируемым параметром является относительная радиальная деформация гибкого колеса по большой оси:

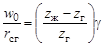, (19.5)

где 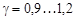— коэффициент относительной радиальной деформации.

Расчетное число зубьев условного колеса равно

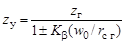. (19.6)

В формуле (19.6), как и во всех последующих, содержащих двойные знаки арифметических действий, верхний знак относится к внутреннему деформированию гибкого колеса дисковым или кулачковым генератором волн, нижний — к внешнему деформированию кольцевым генератором (рис. 19.3, б):

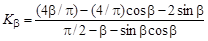, (19.7)

где 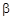— угловая координата участка постоянной кривизны ( ).

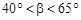Далее определяем радиус серединной окружности деформированного гибкого колеса (см. рис. 19.3):

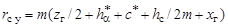, (19.8)

где 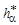, 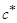— параметры исходного контура; 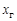— коэффициент смещения исходного контура:

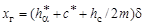, (19.9)

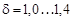— коэффициент смещения.

При изменении величин 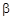, 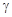и 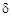в указанных диапазонах их возможного изменения можно провести оптимизацию качества зацепления. Целевой функцией является теоретический коэффициент перекрытия.

Радиус серединной окружности недеформированного гибкого колеса

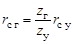. (19.10)

Межосевое расстояние передачи, равное эксцентриситету установки деформирующих дисков, равно

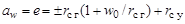. (19.11)

Тогда угол зацепления волновой передачи

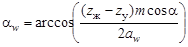. (19.12)

Жесткое колесо в передачах с дисковым или кулачковым генератором внутреннего деформирования, имеющее внутренние зубья, обрабатывается долбяком с числом зубьев 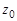. Угол станочного зацепления жесткого колеса и долбяка

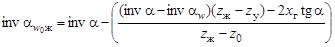, (19.13)

и коэффициент смещения жесткого колеса

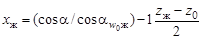. (19.14)

Остальные параметры и исполнительные размеры элементов волновой передачи рассчитывают так же, как зубчатой передачи внутреннего эвольвентного зацепления.

Области применения ВЗП. Отмеченные достоинства волновой передачи определяют наиболее рациональные области ее применения: силовые и кинематические приводы общего назначения с большим передаточным отношением, задающие и исполнительные механизмы повышенной кинематической точности, быстродействующие приводы систем автоматического управления и регулирования, электромеханические приводы промышленных роботов, приводы для передачи движения в герметизированное пространство в химической, атомной и космической технике.