Прямозубом колесе

Расчёты конических зубчатых колес на прочность сводят к расчетам эквивалентных (равнопрочных) цилиндрических прямозубых колес.

если зубья цилиндрического прямозубого колеса и конического прямозубого колеса будут иметь одинаковые сечения (т.е. модуль m_v = m_m) и длину b_V = b_w(рис. 7.6), то они будут обладать равной прочностью. И такое цилиндрическое прямозубое колесо будет равнопрочным исходному коническому колесу, поэтому его называют эквивалентным колесом.

Для определения размеров равнопрочного цилиндрического колеса рассечём коническое колесо дополнительным конусом, образующие которого перпендикулярны образующим делительного конуса исходного колеса и проходят через середину ширины зубчатого венца колеса (см. рис.7.6).

Действительные профили зубьев конических колес в сечениях образующими дополнительного конуса весьма близки к профилям заменяющего эквивалентного цилиндрического колеса. снабдим все параметры эквивалентного колеса индексом “V”.

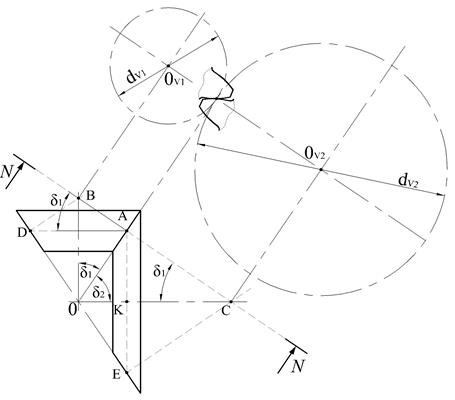
Рис. 7.6. Схема к определению размеров эквивалентного

цилиндрического прямозубого колеса

Длина образующей дополнительного конуса “L_AC” может быть получена из Δ АКС (см. рис. 7.6):

L_AC = L_AK / cos δ₂= 0,5^.d_m2 / cos δ₂ (7.15)

если построить цилиндрическое прямозубое колесо с радиусом делительной окружности, равным длине образующей дополнительного конуса “ L_AC ” (см. рис. 7.6), то и полученное цилиндрическое коле­со будет равнопрочным исходному коническому колесу. Поскольку L_AC = 0,5^.d_2V , то с учетом ф. (7.15) получим:

d_2V = d_m2 / cos δ₂ (7.16)

Аналогичная зависимость для шестерни:

d_1V = d_m1 / cos δ₁ (7.17)

Как известно, делительный диаметр эквивалентного цилиндрического колеса:

d_V2 = m_v·z_v2 (7.18)

Средний делительный диаметр конического колеса:

d_m2 = m_m·z₂ (7.19)

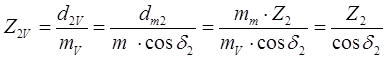Поскольку m_v = m_m , то на основании ф.ф. (7.18) и (7.19) легко установить связь чисел зубьев этих колёс:

(7.20)

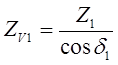Аналогично получим формулу для вычисления числа зубьев эквивалентной шестерни:

(7.21)

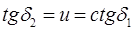Чтобы установить взаимосвязь передаточных чисел, воспользуемся одной из формул (7.1):

и формулами курса “высшей математики”:

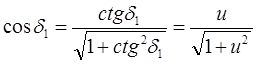
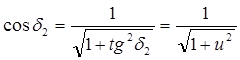
Тогда получим для эквивалентной цилиндрической передачи:

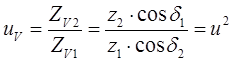(7.22)

межосевое расстояние цилиндрической прямозубой передачи, эквивалентной исходной конической передаче, можно вычислить на основе ф.ф. (7.18) и (7.19):

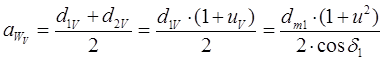
(7.23)

Межосевое расстояние a_WV может быть выражено и через внешнее конусное расстояние R_e конической передачи. Соотношение внешнего и среднего конусных расстояний передачи и соответствующих им делительных диаметров колёс таково (см. рис. 7.7):

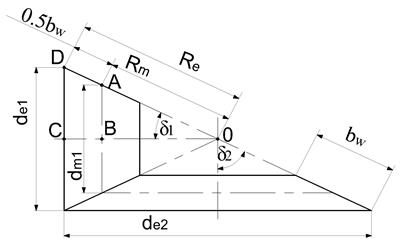
Рис. 7.7. К определению соотношения размеров

конических колёс

Из подобия треугольников Δ АВО и Δ DCОимеем:

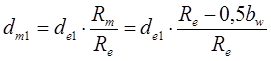
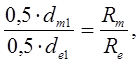
тогда

Диаметр делительной окружнос­ти эквивалентного колеса из ΔОАС (см. рис. 7.6):

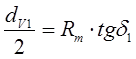
(7.24)

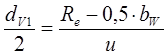здесь R_m = R_e – 0,5·b_W; tg δ₁ = 1/u.

Тогда выражение (7.24) примет вид:

После подстановки его в ф.(8.23) получим:

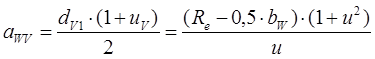(7.25)

Связь между крутящими моментами такова:

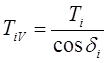(7.26)

Таким образом, определены все параметры эквивалентной цилиндрической прямозубой передачи, необходимые для выполнения прочностных расчетов конической прямозубой передачи.

Расчет конических колес с круговыми зубьями сводится к рас­чету биэквивалентных цилиндрических колёс, т.е. вначале переходят к эквивалентному цилиндрическому косозубому колесу, а затем к равнопрочному цилиндрическому прямозубому колесу. Основные параметры биэквивалентного колеса [2, с. 169]:

1) числа зубьев шестерни и колеса

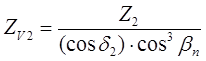
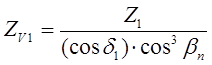
2) делительные диаметры

d_v1 = m_n · Z_v1 d_v2 = m_n · Z_v2

3) межосевое расстояние эквивалентной цилиндрической передачи

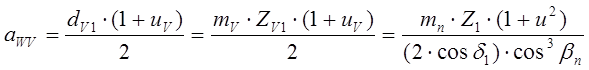
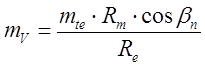4) модуль эквивалентной передачи

7.5. Расчёт зубчатых конических колес на выносливость