Понятие об эквивалентном прямозубом колесе

Расчет косозубого колеса на прочность сведется к расчету равнопрочного с ним прямозубого колеса, которое называется эквивалентным косозубому колесу.

Два цилиндрических зубчатых колеса (прямозубое и косозубое) обладают равной прочностью (при одинако­вых материалах), если имеют одинаковые зубья по длине и по поперечному сечению.

Известно, что зуб косозубого колеса имеет неискажённый эвольвентный профиль только в сечении зуба нормальной плоскостью NN(рис. 24).

Профили зубьев (косозубого и эквива­лентного колес) совпадут, если нормальный модуль т_п косозубого колеса будет равен модулю т_v эквивалентного прямозубого колеса. Снабдим индексом V все параметры эквивалентного колеса. Сечение косозубого колеса плоскостью NN даст эллиптическое се­чение делительного цилиндра с полуосями “c”и “а”(см. рис. 25):

c = d / ( 2 ^.cos β ), а = d / 2 (7.6)

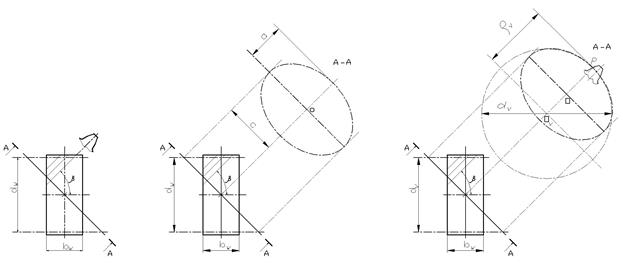
Рис. 25. К определению параметров прямозубого колеса,

равнопрочного косозубому колесу

Радиус кривизны эллипса имеет максимальную величину в полюсе зацепления, точка Р (см. рис. 25):

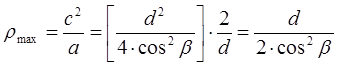(7.7)

Если этот радиус ρ _max принять за радиус делительной окружности, на которой построить профиль эвольвентного зуба с модулем т_v равным нормальному модулю т_писходного косозубого коле­са, то профили зубьев с модулями т_vи т_п полностью совпадут.

Таким образом, из условия совпадения сечений окружность радиусом ρ _max может быть принята в качестве делительной эквивалентного колеса:

d_v = 2 ^.ρ _max= d_v / cos² β (7.8)

Для обеспечения равной прочности зубьев необходимо длину зуба эквивалентного прямозубого колеса принять равной длине зуба косозубого колеса (см. рис. 25):

b_{w v} = b_w / cos β. (7.9)

Связь межосевых расстояний этих равнопрочных передач аналогична связи между делительными диаметрами колес (см. ф.(7.8)):

a_{w v} = a_w / cos ² β.

Соотношение чисел зубьев равнопрочных колес установим путем математических преобразований. Делительный диаметр прямозубого колеса d_v = m_v∙ z_v, отсюда:

Z _v= d_v / m _v (7.10)

Делительный диаметр косозубого колеса d_w = m_n∙z/cos β, отсюда:

m_n=(d∙cos β)/z.

Поскольку m _v = m _n , то подставим это его выражение в (7.10), и с учетом ф. (7.8) получим:

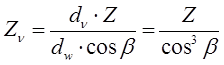(7.11)

Аналогична связь и между крутящими моментами: Т_1V=T₁/∙cos³β.