Движение жидкости в рабочем колесе центробежного насоса

В рабочем колесе насоса частицы жидкости движутся относи­тельно рабочего колеса и, кроме того, они вместе с ним совершают переносное движение. Сумма относительного и переносного движений дает абсолютное движение жидкости, т. е. движение ее относительно неподвижного корпуса насоса. Скорость абсолютного движения υ (абсолютная скорость) равна геометрической сумме скорости ω жидкости относительно рабочего колеса (относительной скорости) и окружной скорости и рабочего колеса (переносной скорости):

υ¯=ω¯+u¯. (5.15)

Для упрощения рассуждений допускаем, что поток в рабочем колесе осесимметричный. При этом траектории всех частиц жидкости в относительном движении одинаковы. Примем, что они совпадают с кривой очертания лопатки АВ (рис. 5.7). Относительные скорости частиц жидкости, лежащих на одной окружности, одинаковы и на­правлены по касательной к поверхности лопатки в рассматриваемой точке. Указанные допущения часто называют схемой бесконечного числа лопаток. В действительности поток жидкости в рабочем колесе не является осесимметричным. Давление на лицевой стороне лопатки (передняя сторона лопатки по отношению к направлению ее движения) больше, чем на ее тыльной стороне. Согласно уравне­нию Бернулли, чем больше давление, тем меньше скорость. Поэтому относительная скорость частиц, движущихся вдоль лицевой сто­роны лопатки, меньше относительной скорости частиц, движущихся вдоль ее тыльной стороны. Относительные траектории частиц, непо­средственно примыкающих к лопатке, совпадают по форме с лопат­кой. Траектории же остальных частиц отличаются от нее.

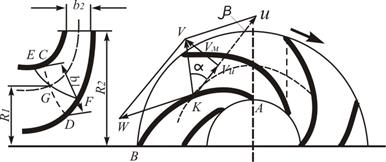
Рис. 5.7. Схема для рассмотрения движения жидкости в рабочем колесе

Из уравнения (5.15) следует, что скорости υ, ω и и образуют треугольник скоростей. На рис. 5.7 изображено сложение скоро­стей для произвольной точки К внутри колеса. Согласно схеме бесконечного числа лопаток, относительная скорость ω направлена по касательной к лопатке. Окружная скорость и направлена по каса­тельной к окружности, на которой расположена рассматриваемая точка, в сторону вращения рабочего колеса.

Разложим абсолютную скорость υна две взаимно перпендику­лярные составляющие: υ_и - окружную составляющую абсолютной скорости и υ_м -меридиональную скорость — проекцию абсолютной скорости на плоскость, проходящую через ось колеса и рассматри­ваемую точку. Эта плоскость называется меридиональной.

Введем следующие обозначения:

α - угол между абсолютнойυ и переносной и скоростями жид­кости;

β - угол между относительной скоростью ωи отрицательным направлением переносной скорости и жидкости;

β_л - угол между касательной к лопатке и отрицательным на­правлением переносной скорости и жидкости.

Введем также индекс 1 для обозначения скоростей и углов на входе в рабочее колесо и индекс 2 для обозначения тех же величин на выходе из него.

Построим треугольник скоростей для точки G входной кромки ЕF рабочего колеса (см. рис. 5.7). Меридиональную скорость υ_м1 опре­делим из уравнения расхода. Принимая распределение меридиональ­ных скоростей по ширине рабочего колеса равномерным, получим

υ_м1= Q_k/S₁= Q/(ŋ_oS₁) (5.16)

где Q_k – расход жидкости, протекающей через колесо; S₁ — площадь нор­мального сечения меридионального потока.

Меридиональным называют воображаемый поток, движущийся через рабочее колесо со скоростями, равными меридиональным. Иными словами, меридиональный поток есть поток, протекающий без окружной скорости через полость вращения, образованную ведомым и ведущим дисками рабочего колеса. Нормальное сечение меридионального потока имеет форму поверхности вращения. Она образована вращением вокруг оси колеса линии СD, пересекающей под прямыми углами линии тока меридионального потока, и про­ходящей через точку G. Согласно теореме Гюльдена, площадь S₀ этой поверхности вращения равна произведению длины b₁ образую­щей СD на длину окружности, описываемой центром тяжести линии СD при ее вращении вокруг оси насоса:

S_o = 2πR_ц1b₁, (5.17)

где R_Ц1 — радиус, на котором расположен центр тяжести линии СD.

Часть поверхности вращения занята телом лопаток, поэтому искомая площадь нормального сечения меридионального потока S₁=ψ₁S_o, где ψ₁- коэффициент стеснения на входе в рабо­чее колесо.

Величина ψ₁ определяется из следующих соображений. Площадь

S1= 2πR_ц1b₁-σ₁b₁z,

где σ₁ - толщина лопатки на входе, измеренная в окружном направлении (рис. 5.8, стр. 220); z - число лопа­ток.

Приближенно из треуголь­ника АВС

σ₁~S₁/sin β_1л,

где S₁ – толщина лопатки на входе, измеренная по нормали к ее поверхности.

Отсюда

ψ₁= S₁/S_o= (2πR_ц1b₁-zσ₁)/( 2πR_ц1 ) (5.18)

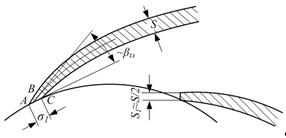
Рис. 5.8. Входной участок лопатки рабочего колеса

У наиболее распространенных насосов величина ψ₁ колеблется от 0,75 (малые колеса) до 0,88 (большие колеса).

Окончательно получим

υ_м1= Q/ (2πR_ц1b₁ψ₁ŋ_o) (5.19)

В п. 5.4 было отмечено, что момент скорости υ_u1R₁ и, следова­тельно окружная составляющая υ_u1 абсолютной скорости на входе определяются конструкцией подвода. Многие разновидности под­вода не закручивают поток, при этом υ_u1 = 0. Окружная составляю­щая абсолютной скорости на входе не равна нулю для спирального подвода и часто для обратных каналов направляющего аппарата, служащих подводом промежуточных сту­пеней секционных насосов.

Окружная скорость рабочего колеса

u₁₌ ωR₁, (5.20)

где ω – угловая скорость рабочего колеса; R₁-радиус, на котором распо­ложена точка G входной кромки колеса (см. рис. 5.7).

Зная величины υ_м1, υ_и1 и и₁, можно построить треугольник скоростей на входе (рис. 5.9) и, следовательно, определить относи­тельную скорость ω₁ и углы α₁ и β₁.

Направление входного элемента лопатки следует выбирать близ­ким к направлению относительной скорости ω₁.В противном слу­чае получается отрыв потока от лопатки с образованием вихревой зоны (см. рис. 5.12, б), сильно увеличивающей потери па входе в рабочее колесо. Опыт показывает, что как КПД, так и высота, на которую насос способен засосать жидкость (высота всасывания), увеличиваются, если входной элемент лопатки рабочего колеса установить по отношению к окружности не под утлом β₁, получаю­щимся из треугольника скоростей входа, построенного для рас­четной подачи насоса, а под углом β_1Л, большим угла β₁ на 3—8°. При таком небольшом отклонении входного элемента лопатки от на­правления относительной скорости отрыва потока от лопатки не полу­чается. Назовем угол менаду направлением относительной скорости и направлением входного элемента лопатки углом атаки.

Начальный участок лопатки утоняют по направлению к входной кромке примерно в 2 раза (см. рис. 5.8) на длине, равной 1/3—1/4 длины лопатки, причем входную кромку лопатки скругляют. Благодаря этому улучшаются ус­ловия обтекания входной кром­ки и уменьшаются гидравличе­ские потери на входе жидкости на лопатки рабочего колеса. Кроме того, при этом увеличи­вается высота всасывания на­соса.

При построении треугольни­ка скоростей входа было учтено стеснение потока лопатками. Следовательно, треугольник скоростей построен для точки, расположенной непосредственно за входом на лопатки рабочего колеса. Для некоторых расчетов необходимо знать относительную и абсолютную скорости потока непосредственно перед входом на лопатки, т. е. потока, не возмущенного лопатками. Введем индекс О для обозначения скоростей этого потока. Учитывая уравнение (5.17), получим меридиональную скорость

υ_м0 = Q/ (S₀ŋ₀)= Q/2πR_ц1b₁ŋ₀ (5.21)

Стеснение потока лопатками не может сказаться на величине окружной составляющей абсолютной скорости. Следовательно,

υ_u0= υ_u1.

Треугольник скоростей перед входом в рабочее колесо изображен на рис. 5.9 штриховой линией. Пунктирная линия показывает направление входного элемента лопатки)

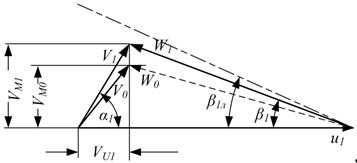
Рис. 5.9. Треугольник скоростей на входе в рабочее колесо (штрих-

Жидкость выходит из рабочего колеса через цилиндрическую поверхность площадью

S₂= 2πR₂b₂ψ₂,

где R₂ - наружный радиус рабочего колеса (см. риc. 5.7); b₂ - ширина канала рабочего колеса на выходе; ψ₂ -коэффициент стеснения на выходе из рабочего колеса.

Коэффициент ψ₂ определяется но уравнению

ψ₂= (2πR₂-zσ₂)/(2πR₂), (5.22)

где σ₂ – толщина лопатки на выходе, измеренная в окружном направлении:

σ₂= S₂/sin β_2л (5.23)

У наиболее распространенных насосов величина ψ₂ колеблется от 0,9 (малые насосы) до 0,95 (большие насосы).

Меридиональная скорость на выходе

υ_м2=Q/(2πR₂b₂ ψ₂ŋ₀) (5.24)

Окружная скорость рабочего колеса на выходе

υ_м2= ωR₂ (5.25)

Окружная составляющая скорости жидкости на выходе из рабо­чего колеса υ_u2 определяется из уравнения Эйлера (5.13) но извест­ному напору насоса. Зная величины υ_м2, u₂ и υ_м2 можно построить треугольник скоростей на выходе из колеса (рис. 5.10, треугольник АDС)и определить из него величину и направление относительной скорости ω₂. Опыт пока­зывает, что направление относительной скорости ω₂ не совпадает с направле­нием выходного элемента лопатки, что не соответcт­вует схеме бесконечного числа лопаток. Причина этого отклонения относи­тельного потока жидкости от выходного элемента лопаток в инерции жидкости. Рабочее колесо закручивает жидкость, увеличивая момент абсолютной скорости υ_uR. Инерция препятствует этому изменению момента скорости. При бесконечном числе лопаток траектории отно­сительного движения предопределены формой лопаток, которые препятствуют иному движению жидкости. При конечном числе лопаток проходы между ними широки, и траектории относитель­ного движения частичек могут отличаться от формы лопаток. В этом случае из-за инерции, препятствующей увеличению момента υ_uR абсолютной скорости, траектории частиц изменяются так, что момент скорости возрастает в меньшей степени. Следовательно, действительное значение окружной составляющей υ_u2 абсолютной скорости на выходе при конечном числе лопаток меньше, чем это следует согласно схеме бесконечного числа лопаток: υ_u2< υ_u2∞.

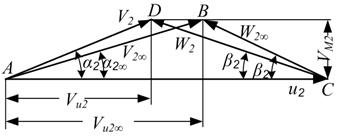
Рис. 5.10. Треугольник скоростей на выходе из рабочего колеса

«Недокрутка» потока из-за конечного числа лопаток, т. е. указан­ное выше уменьшение окружной составляющей абсолютной скорости тем больше, чем шире канал между лопатками рабочего колеса, и, следовательно, тем больше, чем меньше число z лопаток, и больше угол β_л между лопаткой и окружностью (см. рис. 5.16).

Для большинства центробежных насосов «недокрутка» потока из-за конечного числа лопаток может быть приближенно найдена по формуле Стодолы—Майзеля

υ_u2∞- υ_u2 =u₂πsinβ_2л/z (5.26)

Вычислив по уравнению (5.26) окружную составляющую абсолют­ной скорости υ_u2∞ можно построить треугольник скоростей АВС, соответствующий схеме бесконечного числа лопаток. В этом треуголь­нике скоростей относительная скорость ω_2∞ направлена по касатель­ной к выходному элементу лопатки. Из треугольника скоростей опре­деляем угол β_2Л установки выходного элемента лопатки. Зная углы β_1Л и β_2Л, получаем очертание лопатки в плане колеса. Следует отме­тить, что чаще при расчете рабочего колеса центробежного насоса значением угла β_2Л задаются на основании соображений, изложенных в п. 5.7, и определяют такой диаметр колеса D₂, при котором обеспе­чивается заданный напор. Более подробно расчет проточной полости центробежного насоса будет изложен в п. 5.23.

При бесконечном числе лопаток согласно уравнению (5.13) теоре­тический напор насоса

Н_т∞= (ω/g)( υ_u2∞R₂ - υ_u1R₁)(5.27)

Этот напор больше, чем напор при конечном числе лопаток, опре­деляемый по уравнению (5.13), вследствие большей величины окруж­ной составляющей абсолютной скорости на выходе (υ_u2∞> υ_и2).

При прохождении жидкости через рабочее колесо повышается как ее кине­тическая, так и потенциальная энергия (давление). Скорость жидкости на вы­ходе из рабочего колеса равна υ₂, на входе в него υ₁. Следовательно, прирост кинетической энергии единицы веса жидкости, или динамический напор,

Н_дин= (υ₂²-υ₂²)/(2g).

Квадрат абсолютной скорости равен сумме квадратов меридиональной и окружной составляющих. Следовательно,

H_дин=υ²_u2-υ²_u1/2g+υ²_m2-υ²_m1/2g

Меридиональные скорости υ_м2 и υ_м1 сравнительно малы и разностью их квадратов можно пренебречь по сравнению с квадратом скорости υ_u2. По этой же причине часто можно пренебречь квадратом окружной составляющей абсо­лютной скорости на входе υ_u2. Тогда

H_дин= υ²_u2/(2g) (5.28)

Прирост энергии давления единицы веса жидкости при ее прохождении через рабочее колесо, или потенциальный напор,

H_пот= Н_т-Н_дин