Конических передач

Геометрия конических прямозубых колес регламентирована ГОСТ 19624-74, а колес с круговыми зубьями - ГОСТ 19326-73.

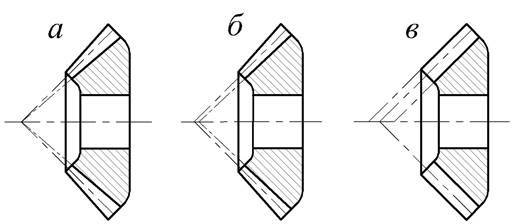
Рис. 7.2. Формы зубьев конических колёс

Геометрия конических колес в значительной степени зависит от осевой формы зубьев, т.е. от изменения размеров сечения зуба по его длине.

Согласно ГОСТ 19326-76 различают зубья трех форм:

Ø форма I – пропорционально понижающиеся зубья (рис. 7.2,а). Вершины делительного конуса и конуса впадин совпадают. Применяют форму I для прямозубых колес, а также для колес с круговыми зубьями при модуле т ≥ 2 мм и числе зубьев шестерни

Z_I = 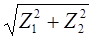=20…100 [4, с. 192];

Ø форма II– понижающиеся зубья (см. рис. 7.2, б). Вершины делительного конуса и конуса впадин не совпадают, а располагаются так, что ширина впадины колеса постоянна по всей длине зуба. Эта форма позволяет обрабатывать одним инструментом сразу две поверхности зубьев, по­этому широко используется в массовом производстве и является ос­новной для колес с круговыми зубьями;

Ø форма III – равновысокие зубья (см. рис. 7.2, в). Образующие конусов (впадин, вершин и делительного) параллельны друг другу. Высота зуба одинакова по всей его длине. Применяют эту форму для колес с круговыми зубьями при Z_I >40[4, с.192].

В конической передаче, как и в цилиндрической, можно опреде­лить поверхность, на которой скорость относительного скольжения зубьев равна нулю (начальную поверхность). Т. к. оси колес пе­ресекаются, то начальные поверхности являются конусами.

В конических передачах угловую коррекцию зубьев не применяют, поэтому начальные и делительные конусы всегда совпадают. Углы делительных конусов обозначаются: δ₁– для шестерни и δ₂ – для колеса.

Для ортогональной передачи (рис. 7.3) Σ = δ₁+ δ₂ = 90°:

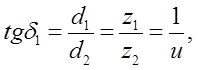
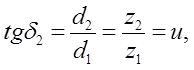(7.1)

Длина образующей делительного конуса от его вершины до боль­шего основания (внешнего торца) называется делительным внешним конусным расстоянием R_e (см. ф. (7.2)).

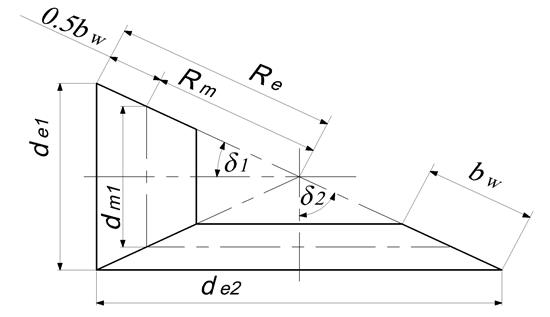
Рис. 7.3. Геометрия конической передачи

Расстояние до середины зубчатого венца – это среднее делительное конусное расстояние R_m . Характеристики не стандартизованы и их определяют с точностью до сотых долей миллиметра.

Для ортогональных передач:

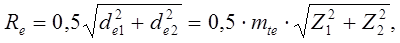
(7.2)

R_m = R_e – 0,5b_w ,

где m _te – внешний окружной модуль;

d_e1, d_e2 – внешний делительный диаметр соответственно: шестерни и колеса.

Вполне понятно, что поскольку колесо коническое, то шаг зубь­ев (и соответственно модуль) может быть измерен по любому сечению зуба вдоль образующей конуса. Таким образом, одно и то же колесо может иметь бесчисленное множество модулей.

С целью удобства на­стройки режущего инструмента при изготовлении конических колес, а также контроля качества выполнения их размеров принято считать базовым внешний торец колеса. Соответственно этому внешний окруж­ной модуль m_te внешний делительный диаметр колеса d_e2 приняты за основные параметры передачи и стандартизованы.

В расчетах передач на прочность используют модуль по середине зубчатого венца и средний модуль m_m (чаще этот модуль обозначают одной буквой, без индекса – m). Следует отметить, что в расчетах одновременно оба модуля округлять до стандартного нельзя. Округляют лишь тот модуль, величина которого ближе к стандартному значению, а другой модуль вычисляют с точностью до сотых долей миллиметра.

В передачах с круговыми зубьями из стандартного ряда назна­чают средний нормальный модуль т_п или внешний окружной т_te:

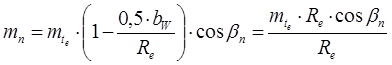(7.3)

Расстояние между внешним и внутренним торцами зуба, измеренное по образующей делительного конуса, называют шириной зубчатого венца и обозначают буквой b_w. Ширину зубчатого венца следует принимать не более 0,3 R_e или 10^.m_е [2, с. 168] и необходимо ок­руглять до стандартной величины по ГОСТ I2289-76.

Прямозубые конические колеса передач общего назначения (при m_е ≥1 мм) выполняют в соответствии с исходным контуром по ГОСТ 13754-81, согласно которому:

α_w= 20°; h_a^*= 1; c^*= 0,2; ρ_f^* = 0,2 (7.4)

Исходный контур конических колес с круговыми зубьями выполняется по ГОСТ 16202-81:

α_n= 20°; h_a^*= 1; c^*= 0,25; ρ_f^* = 0,25(7.5)

Таким образом, основные геометрические размеры конических прямозубых колес вычисляют по зависимостям:

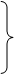1) внешняя высота ножки зуба

h_fe1 = (h_a^*+c^*– x_e1) · m_e, (7.6)

h_fe2 = (h_a^*+c^* + x_e1) · m_e

где x _e1– коэффициент смещения исходного контура; коэффициент смещения для колеса: x _e2= – x _e1 [3, с. 166];

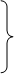2) внешняя высота головки зуба

h_ae1 = (h_a^*+x _e1) · m_e (7.7)

h_ae2 = (h_a^*– x_e1) · m_e

3) внешний диаметр вершин зубьев

d_ae1 = d_e1 + 2h_ae1 ·cos δ₁ (7.8)

d_ae2 = d_e2 + 2h_ae2 ·cos δ₂

4) внешний диаметр впадин зубьев

d_fe1 = d_e1 – 2h_fe1 ·cos δ₁ (7.9)

d_fe2 = d_e2 – 2h_fe2 ·cos δ₂

Конические передачи часто выполняют равно смещенными (x_e2 = – x_e1), что способствует повышению изгибной прочности шестерни.