Конические зубчатые передачи.
Применяются в передачах, где оси валов пересекаются под некоторым углом å. Они сложнее цилиндрических в изготовлении и монтаже. Для нарезания требуются специальные станки и инструмент.
Кроме допусков на размеры зубьев здесь необходимо выдерживать допуски на углы å, d1, d2 (рис.5.38), а при монтаже обеспечивать совпадение вершин конусов. Выполнить коническое зацепление с той же степенью точности, что и цилиндрические значительно сложнее. Пересечение осей валов затрудняет размещение опор. Обычно одно из коническиъх колес располагается консолью. При этом увеличиваются неравномерность распределения нагрузки по длине зуба. В коническом зацеплении действую осевые силы, усложняющие конструкцию опор. Из-за всего этого нагрузочная способность конической зубчатой передачи составляет около 85% от цилиндрической.
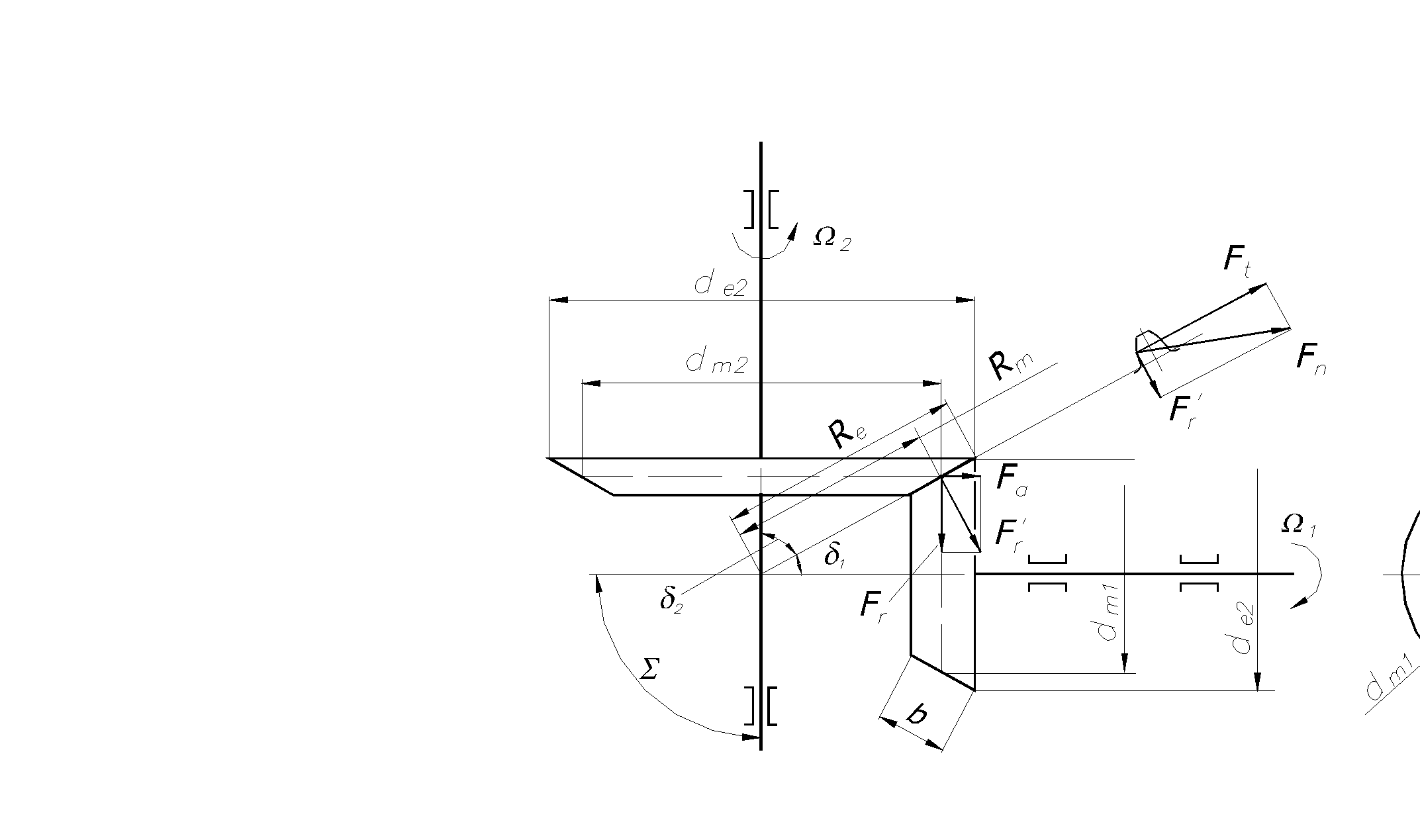
Рис. 5.38
Геометри-ческие осо-бенности прямозубого конического зацепления
Аналогами начальных и делительных цилиндров цилиндрических передач в конических являются начальные и делительные конусы с углами d1, d2.
На рис. 5.39 показан общий вид зацепления.
Рис. 5.39
Общий вид конического зацепления
При коэффициенте смещения инструмента x1+ +x2= 0 начальные и делительные конусы совпадают.
Конусы, образующие которых перпендикулярны образующим делительных конусов называют дополнительными конусами. Сечение зубьев дополнительным конусом называют торцовым сечением. Различают внешнее, внутреннее и среднее торцовые сечения. Размеры, относящиеся к внешнему торцовому сечению сопровождают индексом “e”, например de. Размеры в среднем сечении обозначают индексом “m”, например dm, и прменяют при силовых расчетах.
Используются следующие характерные размеры:
Re= Rm+ 0,5b- внешнее конусное расстояние (Rm - среднее конусное расстояние); de= dmRe/ Rm; mte= mtmRe/ Rm- торцовый модуль зацепления по внешнему дитаметру (mtm - торцовый модуль зацепления по среднему дитаметру). Для прямозубых передач торцовое “t” и нормальное “n” сечения совпадают. При этом значения mte= mnе округляют до стандартного.
Как и у цилиндрических передач, передаточное число равно
u= d2/d1= z2/ z1.
Кроме того, выразив d1 и d2 через конусное расстояние R и углы конусов d1 и d2 , получим
u= sind2/ sind1, (5-56)
а при å= d1 + d2 = 90°
u= tgd2= ctgd1. (5-57)
Силы в зацеплении определяются следующими соотношениями:
/>Ft= 2Mкр1/ dm1- окружная сила;
Fn= Ft/ cosa - нормальная сила; (5-58)
Fr = Ft tga cosd1 - радиальная сила;
Fa = Ft tga sind1 - осевая сила.
Для упрощения расчетов коническое колесо приводят к эквивалентному прямозубому цилиндрическому. Диаметры эквивалентных колес:
due1= de1/ cos d1; due2= de2/ cos d2. (5-59)
Для проектного расчета используют формулу
de2= 1,7 { EnpMкр1КНb u/ [JH [sH]2 (1-Kbe)Kbe]}1/3, (5-60)
где JH =0,85- опытный коэффициент; Kbe - коэффициент ширины зубчатого венца относительно внешнего конусного расстояния. Часто принимают Kbe = 0,285, тогда
de2» 2,9{ EnpMкр1КНb u/ [JH [sH]2 }1/3. (5-61)
Далее рассчитывают диаметр шестерни по среднему сечению
dm1= de2 (1- 0,5 Kbe)/u (5-62)
и толщину шестерни
bw= 0,5Kbe(u2+1)1/2/u..
Контактные напряжения прямозубых конических передач вычисляют по формуле
sH= 1,18{EnpMкр1КН (u2+ 1)1/2/u/(JHd2m1bwsin2a)}1/2£ [sH], (5-63)
Конические колеса могут иметь непрямые зубья. Наиболее распространены колеса с косыми или тангенциальными зубьями и колеса с круговыми зубьями (рис.5.40).
Чаще применяются круговые зубья.
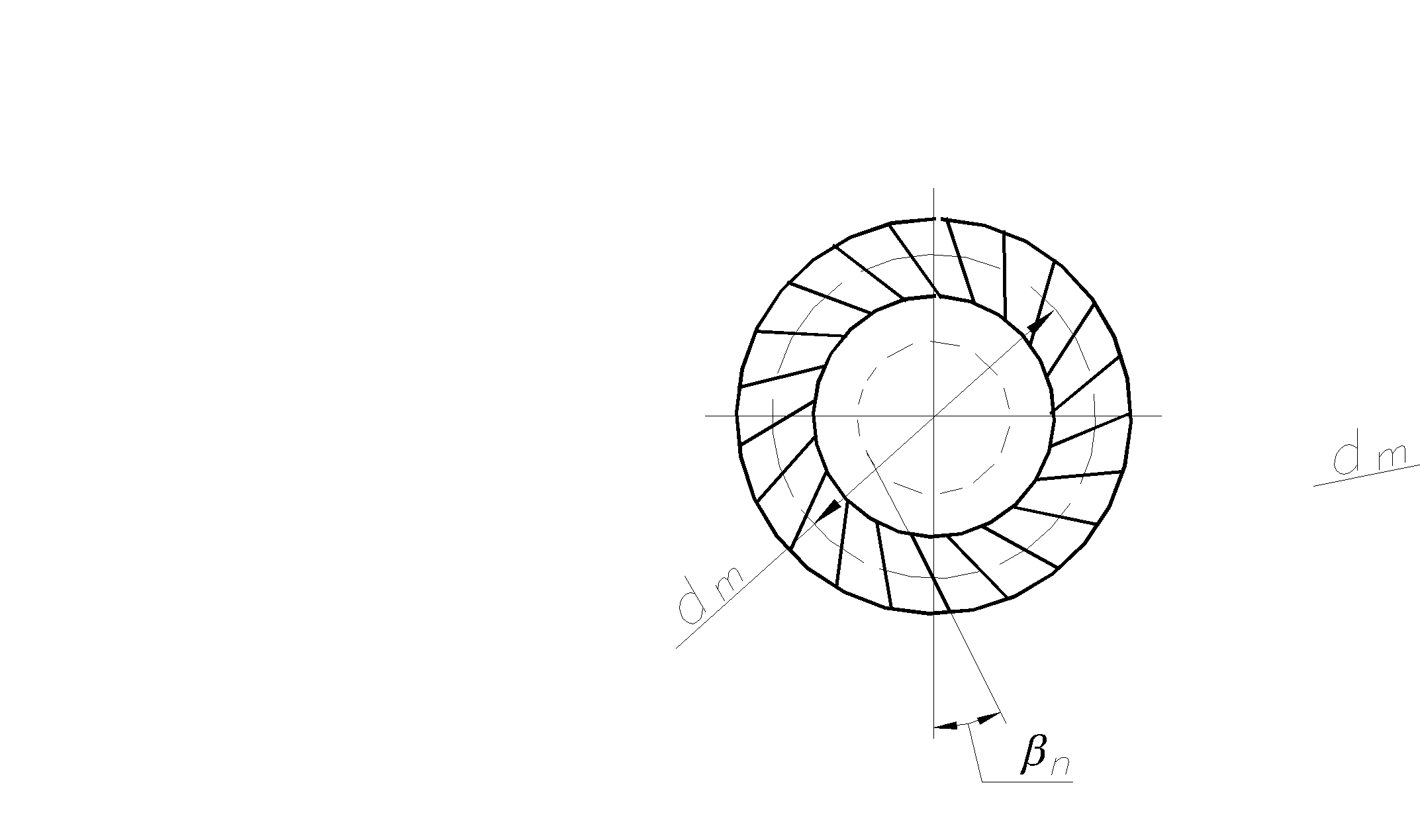
Рис. 5.40.
Колеса с непрямыми зубьями
а) тангенциальные зубья;
б) круговые зубья.
а) б)
Учитывая особое значение выбора m и z, для конических передач с прямозубым и круговым зубом разработаны специальные рекомендации. Сначала по формуле (5-61) определяют de2. Затем из графиков в зависимости от de1= de2/u и u определяют значение z’.
После этого для твердостей колес, не превышающих 350НВ, вычисляют число зубьев шестерни z1= 1,6 z’. В случае более твердых колес предлагаются другие зависимости [4]. В общем случае рекомендуют число зубьев zmin= 17. При этом отсутствует подрезание.
После этого определяется модуль
mm= dm1/z1, (5-64)
на основании которого по ряду выбирается ближайшее значение.
В конических передачах с u>1 для повышения сопротивления заеданию рекомендуют выполнять шестерню с положительнывм смещением (x1> 1), а колесо с отрицательным х2= - х1, причем
x1= xn1» 2(1- u-2)(cos3bn/z1)1/2.
Напряжения при изгибе рассчитываются с помощью соотношения
sF= YFFtKF/(JFbwmm) £ [sF], (5-65)
где JF = 0,85; YF - коэффициент формы зуба [4]; KF= KFbKFu- коэффициент нагрузки определяется по графикам.
Суть работы непрямого зуба такая же, как и у косозубых цилиндрических передач. При этом силы зацепления определяются с помощью соотношений:
Ft= 2Mкр1/ dm1- окружная сила;
Fr = (Ft /cosbn)(tga cosd1± sinbnsind1)- радиальная сила; (5-66)
Fa = (Ft /cosbn)(tga sind1± sinbncosd1)- осевая сила.
Расчет прочности выполняют по параметрам биэквивалентных цилиндрических прямозубых колес:
dun= de/ (cosd cos2bn) - диаметр;
zun= z/ (cosd cos2bn)- число зубьев.
Для круговых зубьев контактные напряжения вычисляют по специальным формулам.
Дата добавления: 2015-02-23; просмотров: 1583;
