О колебаниях в станке глубокого сверления
«KOLB- HTB III WE».
В главе 3 рассматривалась динамика узлов и механизмов, из которых состоит машина. В этом разделе дается пример анализа динамики машины- станка глубокого сверления.
В последние годы часто изготавливают теплообменные аппараты, доски трубные (коллекторы) которых имеют значительную до 500 мм толщину. Сверление многих тысяч отверстий в таких изделиях представляет серьезную задачу. Получить систему качественных отверстий можно при устойчивом функционировании всех узлов станка глубокого сверления.
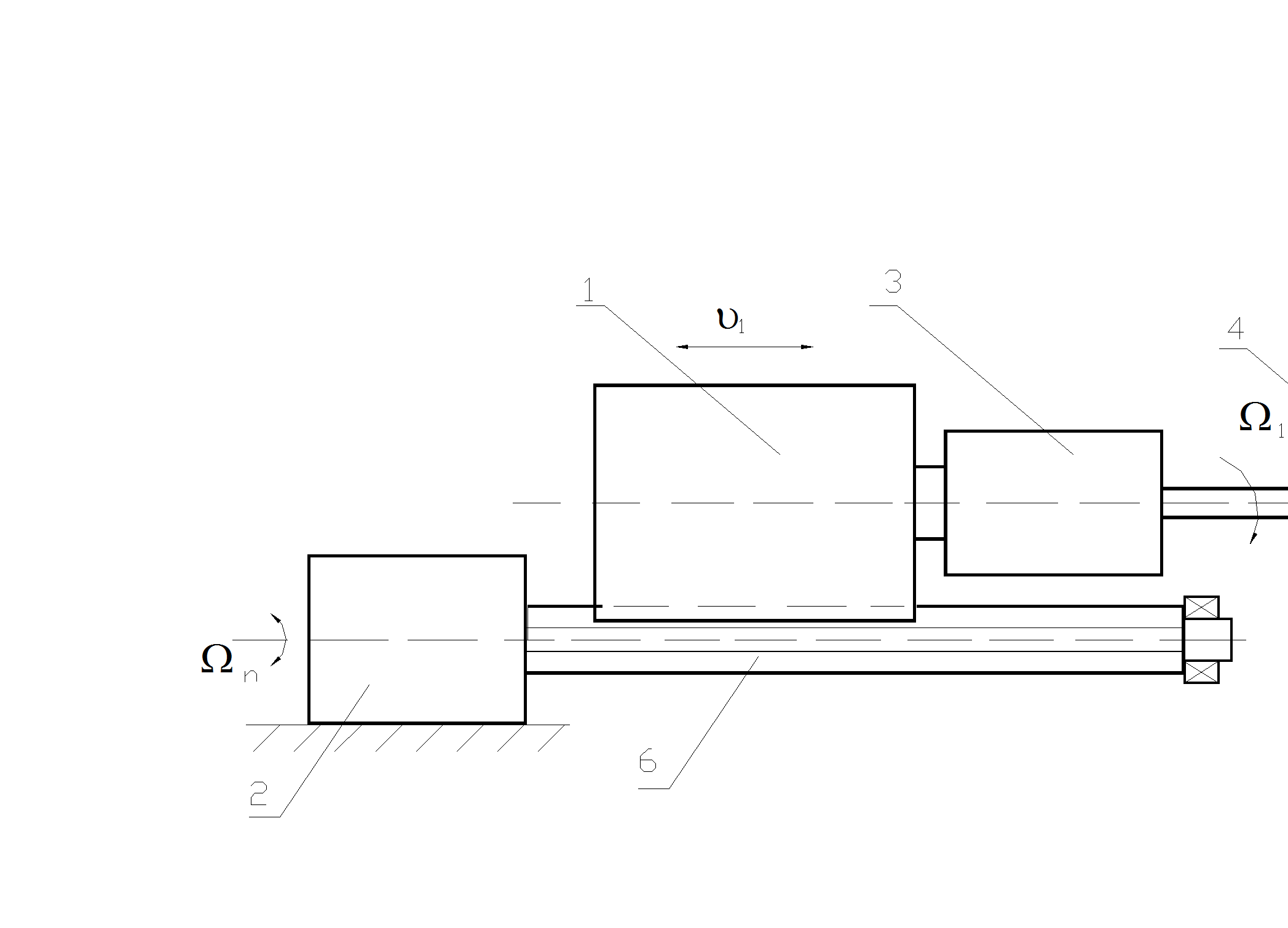
Рис.5.12 Схема привода сверла для глубокого сверления:
1- основной электродвигатель; 2- электродвигатель осевой подачи;
3- шпиндель; 4, 5- стебель и режущая часть ружейного сверла; 6- ходовой
винт.
Такую работу успешно выполняют с помощью «KOLB- HTB III WE». Однако при некоторых условиях в процессе сверления могут возникать неустойчивые режимы. Схема приводов станка приведена на рис.5.12.
В связи с тем, что у всех электродвигателей частота вращения падает с ростом крутящего момента (см. рис. 5.11), то при анализе это обстоятельство необходимо учитывать[14].
Известно, что на плоский проводящий замкнутый контур, помещенный в однородное магнитное поле, действует момент сил
® ® ®
М= Рm В, (5-27)
где Pm- вектор магнитного поля контура; В- магнитная индукция.
Учитывая уравнение (5-27), можно утверждать, что крутящий момент, действующий на ротор электродвигателя, равен М= f1(B), где f1(B) - некоторая непрерывная функция от магнитной индукции.
В общем случае вращающееся магнитное поле (движитель) в электродвигателе преодолевает суммарное сопротивление
f1(B)= Mc + hsWд+ JдdWд /dt, (5-28)
где Мс- момент сопротивления; hs - потери на трение в нагрузке и двигателе, пропорциональные скорости вращения; Jд - приведенный момент инерции вращающихся частей.
Если рассматривать установившийся режим и полагать, что потери момента от скорости малы, то f1(B)= Mc , а в отклонениях от установившегося режима
DМс= (¶ f1/ ¶B)DB= KВМDВ. (5-29)
Обратившись к механическим или скоростным характеристикам, приведенным на рис.5.11, можно записать Wд= f2(Mc).
Рассматривая отклонения, получим
DWд= (¶ f2/ ¶ Mc) D Mc = (¶ f2/¶ Mc)KВМDВ.
Перепишем в отклонениях уравнение (5-28) и полученное выражение с учетом изложенного:
KВМDВ = DMc + hsDWд+ Jдd(DWд )/d t,
DWд=DWп - КВМ (¶ f2/ ¶ Mc ) DB=DWп - КВП КВМDВ,
где DWп – отклонения частоты вращения магнитного движущего поля в электродвигателе; КВП= ¶ f2/¶Mc- тангенс наклона механической характеристики в конкретной ее точке.
Удалим, для простоты символ “D” и введем оператор pº d/dt
KВМВ(t) = Mc (t) + hs Wд (t)+ JдpWд (t), (5-30)
Wд(t) =Wп(t) - КВП КВМВ(t). (5-31)
Решив алгебраическим способом эту систему, получим уравнение скорости вращения вала электродвигателя
Wп(t) - КВП Mc (t)= Wд(t)+ КВП [hs Wд (t)+ Jдd(Wд )/dt]. (5-32)
Если в силовой электрической цепи имеются заметные емкости, индуктивности или и то и другое, то в уравнение (5-31) следует добавить член, зависящий от скорости изменения магнитной индукции. Тогда в левой части уравнения (5-32) появится слагаемое со второй производной.
Обратившись теперь к приводам на рис. 5.12, запишем в операторном виде систему дифференциальных уравнений, описывающих работу станка:
крутильные колебания режущей части
t(t)Wp- hk1W2 (t)(1+ T1p)= Mc (t); (5-33)
- t(t) WpJkp+ W1(t) - W2(t) = 0; (5-34)
продольные колебания режущей части
s(t) f- hп1u2(t) (1+ Т11р)= Fc2 (t); (5-35)
u1(t)- u2(t)- fJпps(t)= 0; (5-36)
колебания в электродвигателе осевой подачи
KBM2B2(t) – hs2u1(t)(1+ T2 p)= k mf -1 Fc2(t); (5-37)
u1(t)+ J2 kuW -1 pB2(t)= Wп1 kuW-1 ; (5-38)
колебания в основном электродвигателе
KBM1B1(t) – hs1W1(t)(1+ T21 p)= Мс1(t); (5-39)
W1(t)+ J1pB1= Wп((t), (5-40)
где Fc2= kfm Mc; T1= J11/hk1; T11= m12 /hп1; hs2= (hп2+ hп1)/ kuW ; Wп, Wп1- частоты вращения магнитного поля в основном электродвигателе и электродвигателе подачи; T2= Js2/(hп1+hп2); Js2 - приведенный к валу электродвигателя подачи маховой момент инерции вращающихся и поступательно перемещающихся частей; kuW - коэффициент, переводящий продольную скорость движения шпинделя в частоту вращения вала электродвигателя подачи; kmf - коэффициент, учитывающий взаимосвязь крутящего момента сопротивления на режущей части и осевой нагрузкой сверла, т.е. Fc2=kmf Mc; hs1= hk1+ hk2- коэффициент потерь на трение, пропорциональное скорости вращения вала основном электродвигателе и нагрузке; T21= Js1/hs1; Js1 – маховой момент инерции вращающихся частей, связанных с валом основного электродвигателя; f- сечение стебля; J11, m12 – маховой момент инерции и масса режущей части сверла; J 1= КВП1 КВМ1 /p; J 2= КВП2 КВМ2 /p; Jп= Jпо = lE -1f -1 - продольная упругость; Jk= Jk0 = l/(GrWp2)- крутильная упругость для цилиндрического стержня.
Введем переменные
x1= B1 ; x2= W1; x3= t; x4= W2; x5= B2; x6= u1; x7= s; x8= u2.;
A14= -hk1(1+T1p); A38= -hп1(1+T11 р); A23= - WpJ k p; A72= -hs2(1+T21p);
A56= - hs2(1+T2 p); A65= J 2 kuW-1p; .A81= J 1 p; A55= KBM2; A71= KBM1;
A47=-fJ п p; F’c2= Fc2 /kmf ; W’п= Wп1 /kuW .
Перепишем систему уравнений (5-33) – (5-40) в векторной форме
A х(t)= M(t), (5-41)
где х-вектор переменных; M-вектор внешних воздействий,
A= 
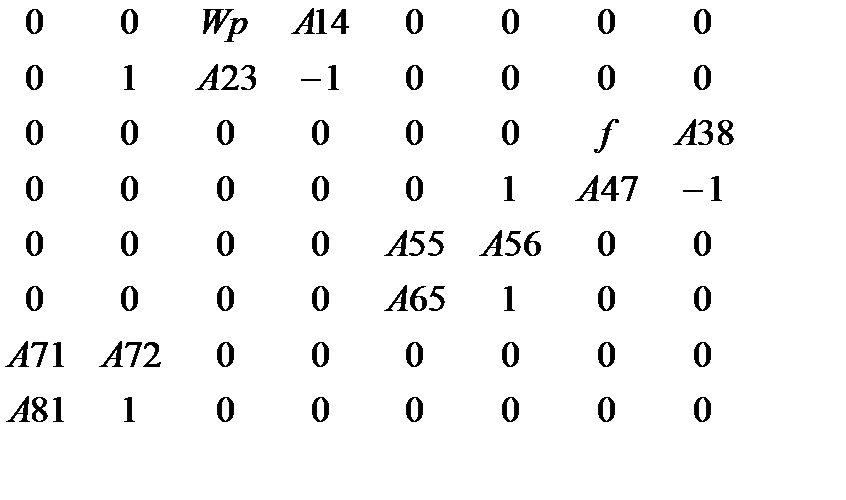-матрица коэффициентов.
Y AKs5Yeth7YiQ/RqCS+XxoAZD7r4aQTjf5/F8PVvPslGWTtejLC7L0d1mlY2mm+RmUr4pV6sy+eFT S7K8Foxx5bM7iTjJ/k4kwzj18jvL+IqFvSS7Cc9Qwwu36DqN0DfgcvoGdkEtXiB+PG2+1ewZxGJ0 P5Vwi8Ci1uYFow4mssD2254YjpF8r0Dy8yTL/AiHTTa5AWkic2nZXlqIogBVYIdRv1y5fuz3rRG7 GiIloa1Ke7VXwp3U3Gc1SBumLjAYbgg/1pf74PXrHlv+BAAA//8DAFBLAwQUAAYACAAAACEAe/oE it0AAAAJAQAADwAAAGRycy9kb3ducmV2LnhtbEyPy07DMBBF90j8gzVI7KiTIIU0jVOhIhaIFeUh sXOTaRwRj0M8bQNfz7CC5dW5unOmWs9+UEecYh/IQLpIQCE1oe2pM/DyfH9VgIpsqbVDIDTwhRHW 9flZZcs2nOgJj1vulIxQLK0BxzyWWsfGobdxEUYkYfswecsSp063kz3JuB90liS59rYnueDsiBuH zcf24A00r/z9huFR36HjZJN9vhPrB2MuL+bbFSjGmf/K8Ksv6lCL0y4cqI1qMJAVN0upGihyUMKv 01TyTsAyz0HXlf7/Qf0DAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAA AAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAA CwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEAwBD5OnsCAAAPBQAA DgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAe/oEit0AAAAJ AQAADwAAAAAAAAAAAAAAAADVBAAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAN8FAAAA AA== "/> x(t)=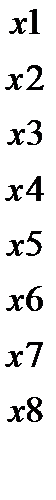 
; M(t)= 
.
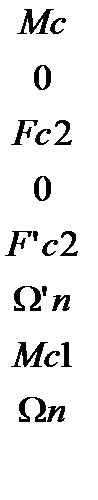Решим определитель D, по форме равный матрице А:
D= fWpKBM1KBM2(1+KВП1hs1 + KВП1Js1p)(1+hk1Jkp+ JkJ11p2)x
x(1+KВП2hs2kuW-1 + kuW-1 KВП2Js2p)(1+hп1Jпp+ Jпm12p2). (5-42)
В силу физической реализуемости D¹ 0. Поэтому неизвестные переменные по правилу Крамера могут быть найдены из выражений:
x1= B 1= D1/D; x2= Wд = D2 /D; x3= t= D3 / D; x4= W2= D4 /D,
x5= B2= D 5 /D ; x6= u1= D6 /D; x7= D7/ D; x8= D8 /D,
где определители Di получаются подстановкой в матрицу А столбца воздействий вместо столбца соответствующей искомой переменной.
Так, для продольных колебаний скорости перемещения двигателя осевой подачи u1 получим
D6= (А71- А81А72)(-Wp- A23A14)(A55W’п- A65F’c2)(-f- A38A47)=
= KBM1KBM2 f Wp(1+ KВП1hs1+ KВП1Js1 p) (1+Jkhk1p+
+J11Jk p2) kuW-1 (Wп1- KВП2Fc2)f(1+Jпhп1p+Jпm12p2) (5-43)
Откуда колебания скорости поступательного движения шпинделя
u1(t)= kuW-1 [Wп1(t)- KВП2Fc2 (t)]/{ (1+KВП2hs2kuW-1 +
+kuW-1 KВП2Js2p)(1+hп1Jпp+ Jпm12p2)}. (5-44)
Для колебаний частоты вращения режущей части W2 получим
W2(t)= [(1+ KВП1hs1+ KВП1Js1 p) JkpMs – KВП11 Мс1+ Wп]/
/[(1+KВП1hs1 + KВП1Js1p)(1+hk1Jkp+ JkJ11p2)]. (5-45)
Колебания максимальных касательных напряжений в стебле будут
t = W-1p[ (KВП1Мс - Wп)hk1(1+T1p)+ Mc(1+ КВП1hs1+ КВП1 Js1p)]/
/[(1+KВП1hs1 + KВП1Js1p)(1+hk1Jkp+ JkJ11p2)]. (5-46)
Резонансы могут наблюдаться при частотах
w1 =(Jпm12)-1/2; w2 =(JkJ11)-1/2. (5-47)
Применяя изложенный прием можно описать линейные колебания других переменных, и с учетом полученных знаний правильно спроктировать и эксплуатировать станок.
Зубчатые передачи. Основные понятия
В разделах 5.4- 5.12 изучаются методы расчета зубчатых передач на прочность и долговечность, полагая, что геометрия зацепления и способы изготовления известны из курса “Теория механизмов и машин”.
Существуют разнообразные зубчатые передачи: с параллельными осями, с пересекающимися, прямозубые, косозубые, эвольвентные, круговые ... .
Все понятия и термины, относящиеся к геометрии и кинематики, стандартизированы. Существуют также стандартные методы расчета. Однако из-за сильной детализации такие методы здесь не рассматриваются. За базовый метод расчета принята книга Иванова М.Н. [4].
Принцип действия зубчатой передачи основан на зацеплении пары зубчатых колес (рис. 5.13).
На рис. 5.13,а показана зубчатая цилиндрическая пара с наружными прямыми зубьями на обоих колесах. На рис. 5.13,б показана зубчатая цилиндрическая пара с прямыми зубьями, причем ведущее колесо, называемое шестерней, имеет наружные зубья, а ведомое колесо имеет зубьяв, нарезанные на внутренней поверхности колеса. На рис. 5.13,в показано зацепление шестерни с зубчатой рейкой.
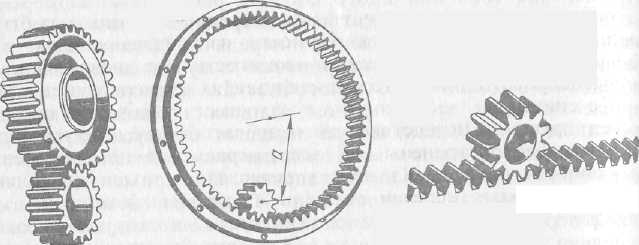
а) б) в)
Рис. 5.13. Зубчатое зацепление: а) внешнее; б) внутреннее; в) с рейкой.
Рассматривая зубчатые передачи, обычно предполагают, что это редукторы. Чаще всего под редуктором понимают устройство, снижающее частоту вращения. Хотя возможно и повышение оборотов, но тогда подобное устройство обычно называют мультипликатором. На рис. 5.14- 5.32 изображены схемы различных зубчатых передач.
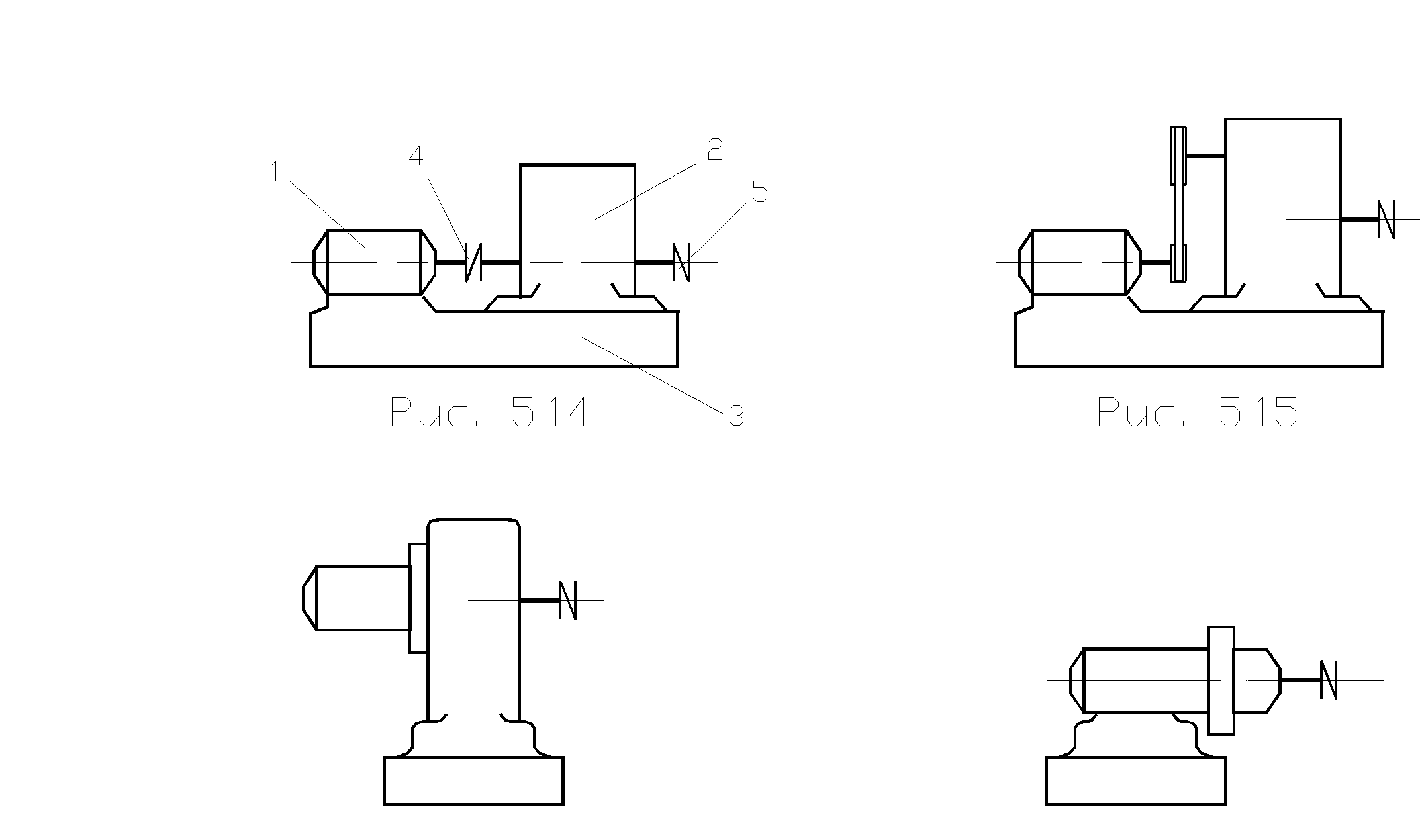
На рис. 5.14, где показан привод, состоящий из электродвигателя и редуктора, валы которых соединены муфтой, применены следующие обозначения: 1- двигатель; 2- редуктор; 3- станина; 4, 5- соединительные муфты. В последующих рисунках подобные фигуры означают отмеченные узлы.
В приводе на рис. 5.15 электродвигатель и редуктор соединены с помощью ременной передачи. Привод может быть выполнен таким образом, что электродвигатель будет закреплен на корпусе редуктора (рис. 5.16) или же редуктор с помощью фланцев окажется прикрепленным к редуктору (рис. 5.17). В таком случае это будет мотор- редуктор.
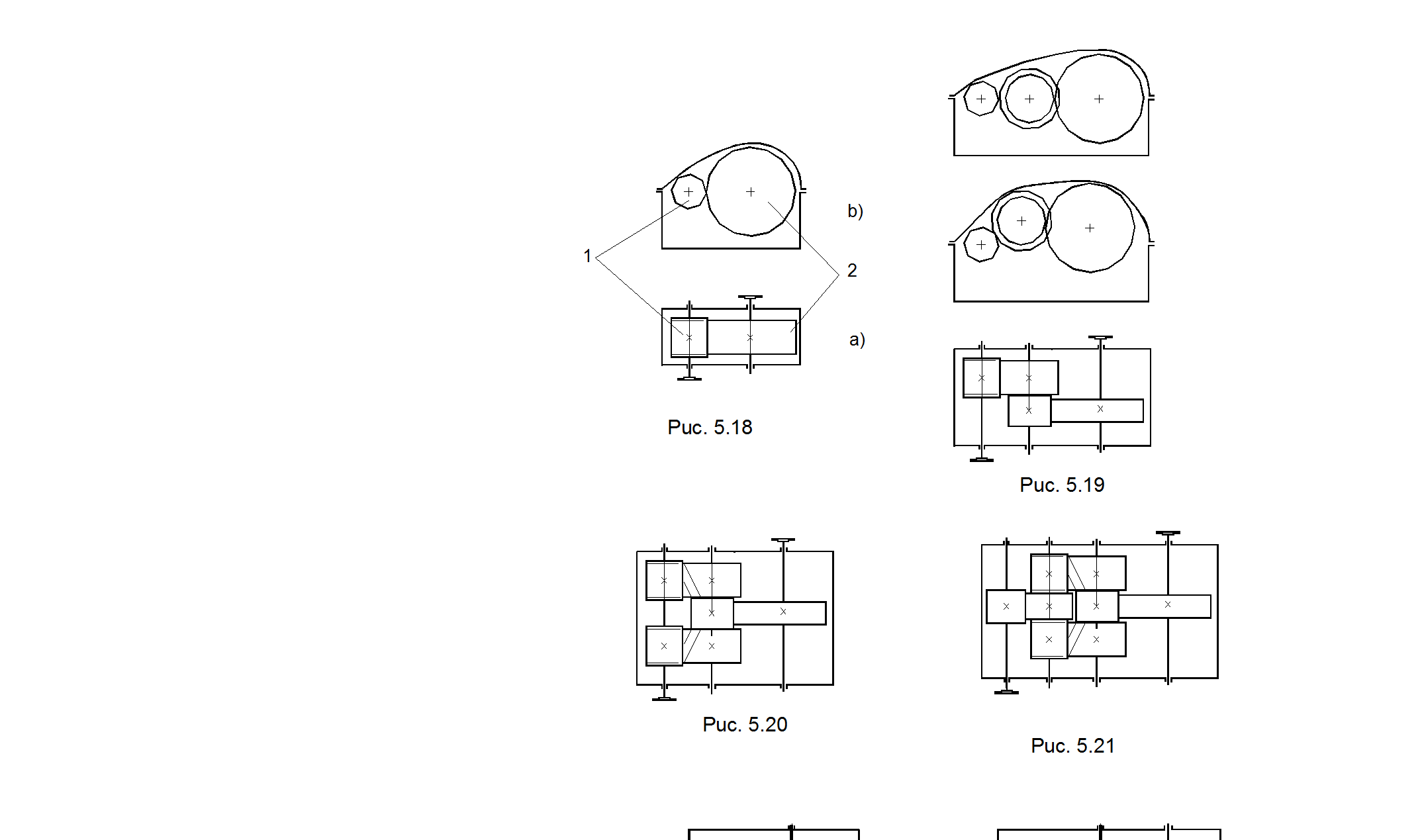
На рис. 5.18 показана схема цилиндрического одноступенчатого зубчатого редуктора. Здесь мощность через соединительную муфту подводится к шестерне 1, затем через колесо зубчатое 2 передается по валу к выходной муфте, к которой присоединяется какой-либо исполнительный орган. Причем на рис. 5.18,а показан вид со снятой крышкой, а на рис.5.18, б – продольный разрез.
На рис. 5.19 изображена схема 2-х ступенчатого однопоточного цилиндрического редуктора. Здесь также приведено различное положение промежуточного вала.
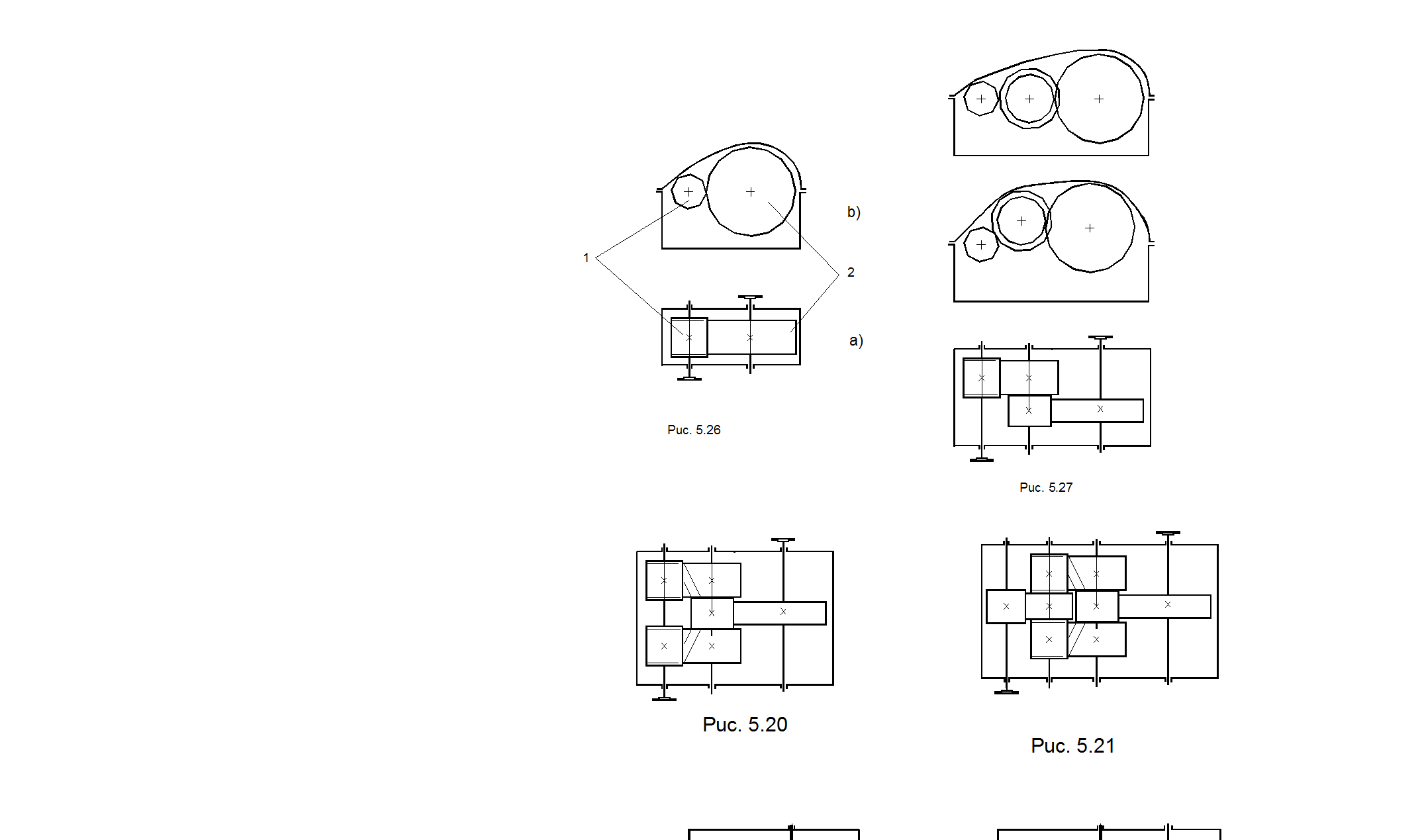
На рис. 5.20 изображена схема 2-х ступенчатого редуктора с цилиндрической зубчатой передачей с разделением подводимой мощности на 2 потока и последующим ее суммированием на выходном вале.
На рис. 5.21 показана схема 3-х ступенчатого редуктора, где на 2-м и 3-м валах мощность разделена на два потока, а на выходном вале она суммируется.
Схемы редукторов с конической зубчатой передачей приведены на рис. 5.22- 5.25. При этом на рис. 5.22 изображена схема с консольным расположением шестерни, а на рис. 5.24 шестерня размещена между опорами. В первом случае имеет место компактная конструкция, но в ней возможен недопустимый прогиб вала шестерни, во втором- усложнена конструкция. На рис. 5.23 (вид сверху), 5.25 (продольный разрез) показана схема двухступенчатого коническо- цилиндрического редуктора. Причем первой ступенью является коническая пара, а второй- цилиндрическая.
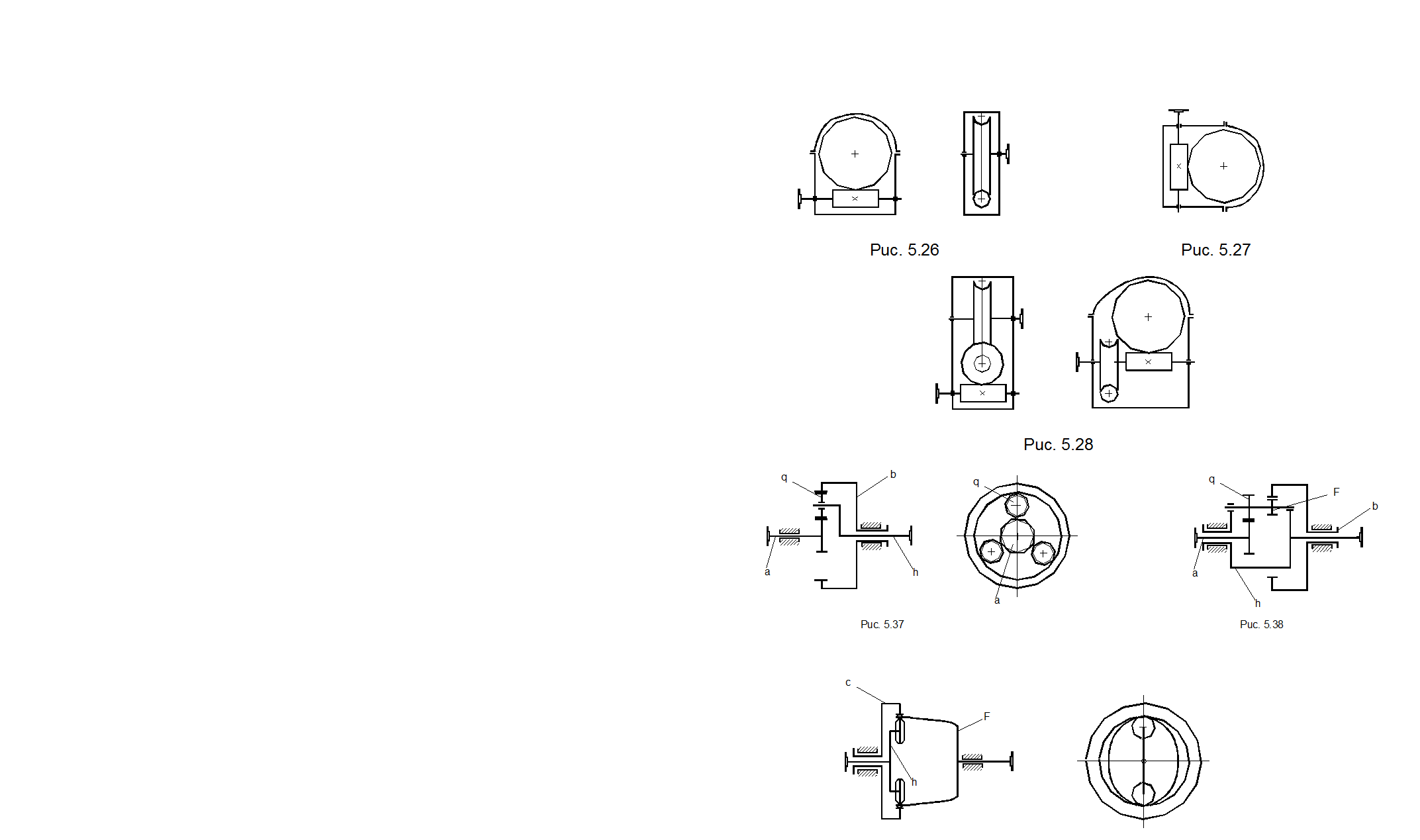
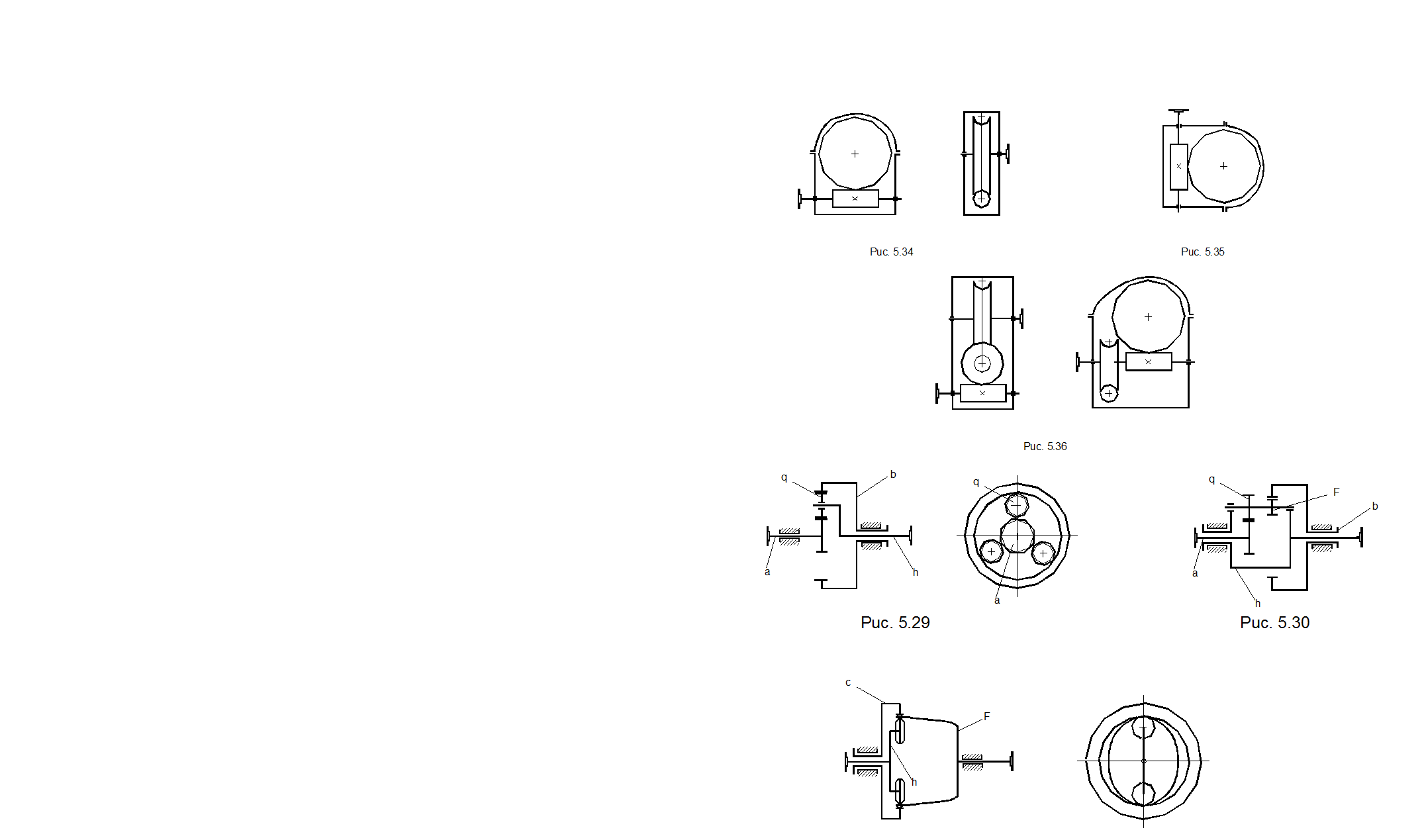
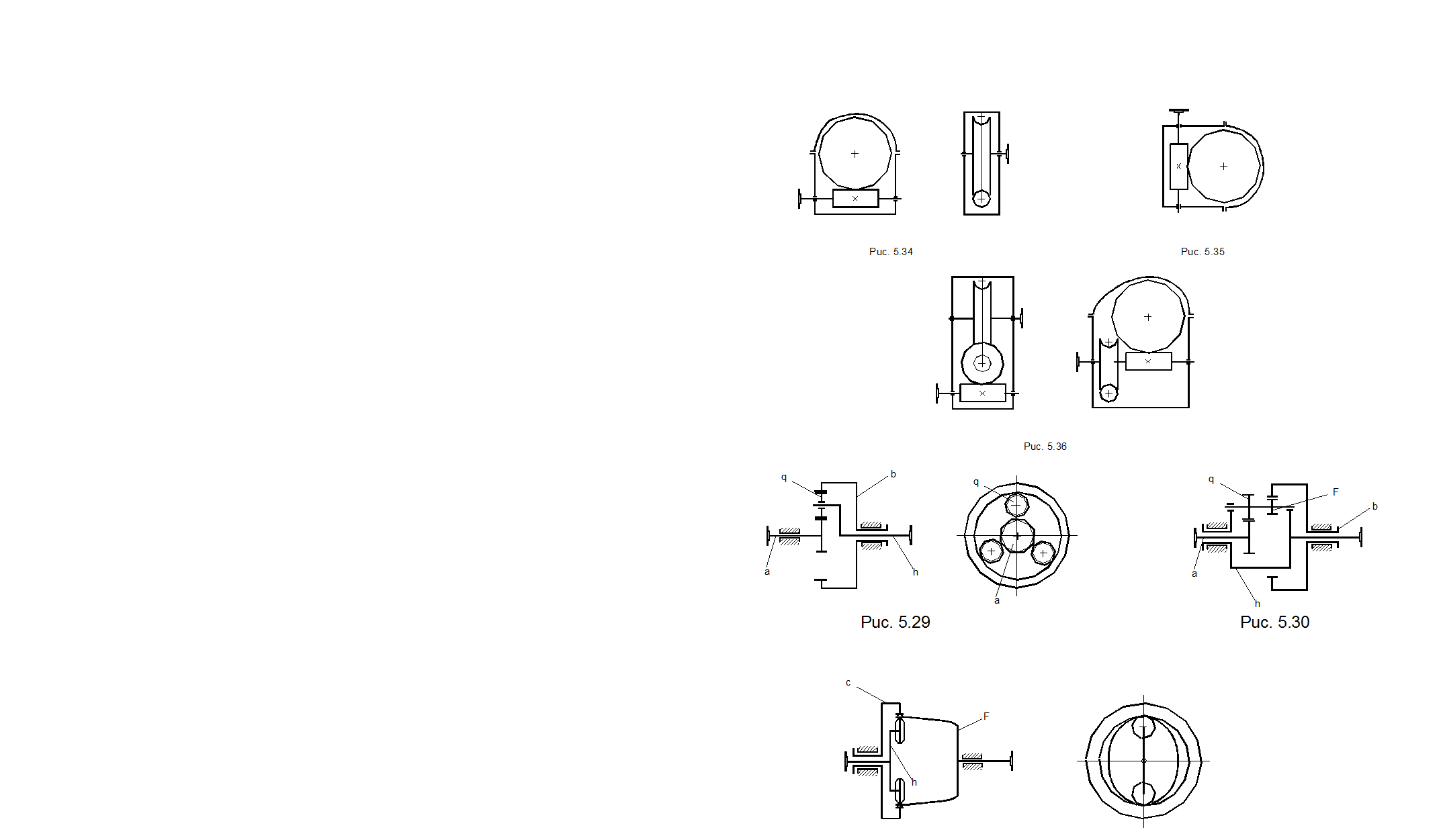
На рис. 5.26- 5.28 показаны различные схемы одноступенчатого и двухступенчатого червячных редукторов
Различные схемы планетарных редукторов приведены на рис. 5.29, 5.30. Здесь обозначены: а- центральное колесо с наружными зубьями; b- центральное колесо с внутренними зубьями; h- водило; q- сателлиты.
На рис.5.31, 5.32 изображены схемы волновых редукторов.
5.5. Цилиндрические зубчатые передачи [4].
Простейшая зубчатая передача состоит из 2-х зубчатых колес. При этом меньшее колесо называют шестерней, а большее- колесом. Обычно шестерня является ведущим звеном, а колесо- ведомым. Поэтому параметры шестерни имеют нижний индекс “1”, а колеса- “2”.
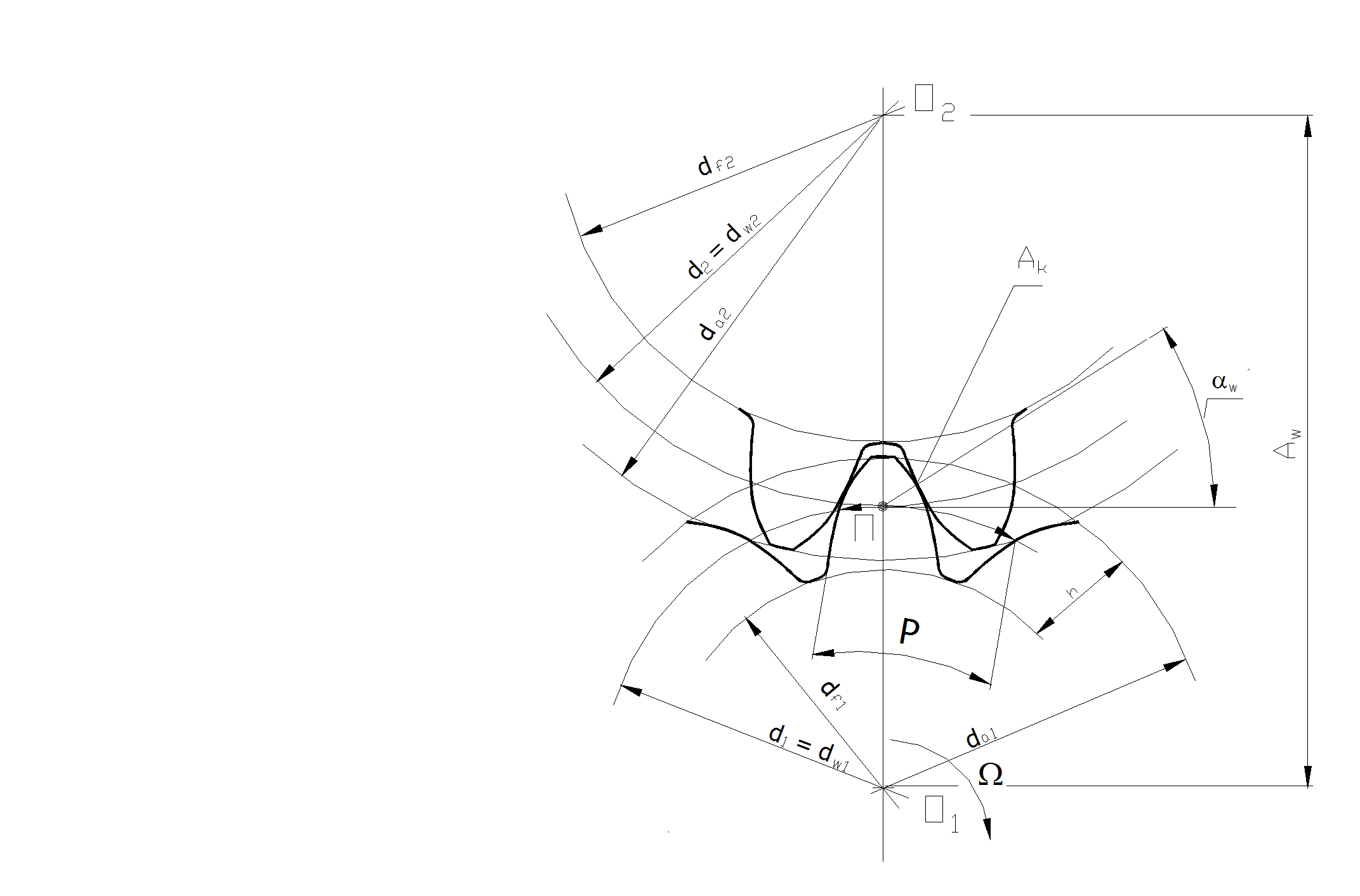
На рис. 5.33 показано взаимодействие зубьев шестерни и колеса.
Здесь Р является делительным шагом; dw1, dw2- начальные диаметры соответственно шестерни и колеса, по которым пара зубчатых колес обкатывается в процессе вращения. При этом, если нет смещения или оно в сумме равно нулю, то начальные диаметры равны делительным диаметрам, т.е. dw1= d 1, dw2 = d2. На рис. 5.33 изображен такой случай. (При нарезании со смещением делительная плоскость рейки (делительная окружность инструмента) смещается к центру или от центра заготовки на величину xm). П- полюс зацепления.
|
а)
б) в)
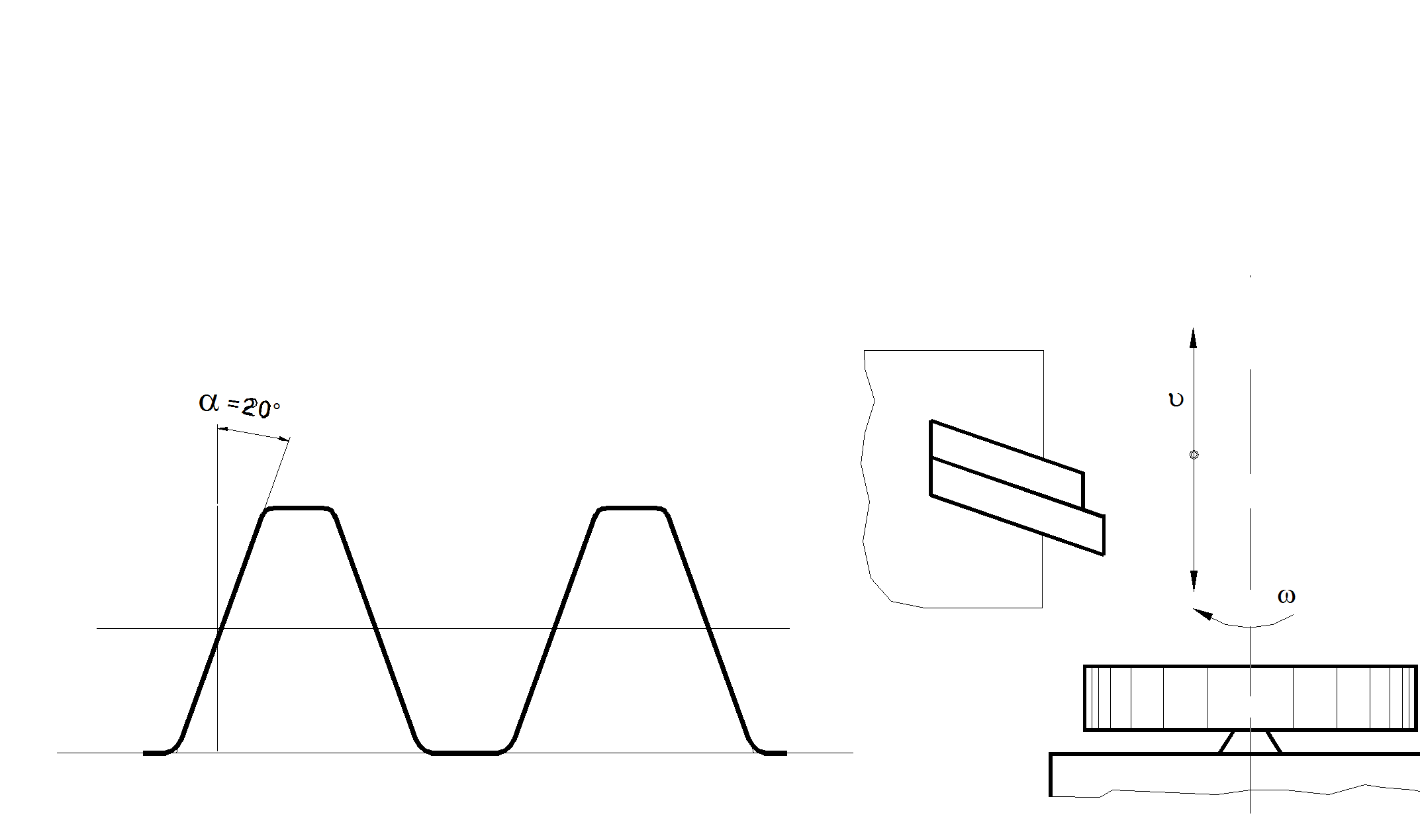
Рис. 5.33 Зубчатое зацепление:а) геометрия зацепления; б) рейка для нарезания зубьев; в) схема нарезания зубьев
Профиль зуба показанного зацепления называется эвольвентным.
Окружным модулем зубьев (основной характеристикой их размеров) называют соотношение m= P/p. Его значения стандартизированы. Так как на длине делительной окружности укладывается z зубьев, то pd= Pz, откуда следует d= Pz/p= mz - делительный диаметр.
Угол aw называется углом зацепления или углом профиля начальным. Обычно aw= 20°.
Расстояние между осями ОО1 равно A= 0,5(dw1 + dw2).
Если нет смещения[15] , то А= Aw = 0,5 m(z1+ z2); h= 2,25 m- высота зуба; da= d+ 2m- диаметр вершин зубьев; df= d- 2,5m- диаметр впадин зубьев.
Контактные напряжения образуются в точке Ак в месте соприкосновения криволинейных поверхностей зубьев. Максимальное контактное напряжение можно определить из выражения
sH= {q(rпрp)-1E1E2/[E1(1- c22)+ E2(1- c21)]}1/2 » 0,418 (qEпрr-1пр)1/2, (5-32)
где c= 0,25...0,35 - коэффициент Пуассона; Eпр= 2E1E2 /(E1+ E2)- - приведенный модуль упругости; r-1пр= r-11± r-12- приведенная кривизна; q - удельная по длине нагрузка.
Знак “-“ используется тогда, когда поверхность зуба вогнута (зацепление Новикова).
При вращении в точке контакта Ак поверхность под действием нормальной силы периодически нагружается и разгружается, а контактные напряжения изменяются прерывисто от нуля до некоторого максимального значения. Кроме того, при передаче крутящего момента в зацеплении действует сила трения, связанная со скольжением и качением. Причем 1-я максимальна. Эти обстоятельства приводят к переменным высоким нагрузкам в зоне контакта, изгибающим напряжениям в основании зуба. В совокупности действующие силы вызывают усталость поверхностных слоев металла и металла в основании зуба и, как следствие, появление потертостей, трещин, поломок зубьев. В случае появления трещины масло, если оно используется в редукторе, проникает в микротрещины и при обкатывании создает в образующейся полости высокое давление, приводящее к дополнительному возрастанию трещины....
Решающее влияние на работу зубчатых колес оказывают контактные и изгибающие напряжения. В процессе работы могут быть поломки зубьев; усталостное выкрашивание рабочих поверхностей; абразивный износ; заедание (развивается из-за высокой температуры в зоне контакта, приводящей к свариванию).
Расчетной нагрузкой называется такая нагрузка, при которой имеет место максимальная удельная нагрузка, распределенная по линии контакта зубьев
q= FnK/ lå, (5-33)
где Fn - нормальная сила в зацеплении; K= Кb Кu -коэффициент расчетной нагрузки (для контактной нагрузки он записывается в форме KН = КНb КНu ;для изгибающей нагрузки- в форме KF = КFb КFu); Кb - коэффициент концентрации нагрузки; Кu - коэффициент динамической нагрузки; lå - суммарная длина линии контакта.
Концентрация или неравномерность распределения нагрузки по длине зуба связана с деформацией валов, корпусов, опор, зубчатых колес, погрешностями изготовления передачи.
В общем виде Кb= qmax/ qcp.
При постоянной нагрузке и HB< 350 и u< 15 м/с Kb= 1.
Коэффициент Кu определяют из соотношения
Кu= 1+ qu / q,
где qu , q - удельные динамическая и расчетная в зоне ее наибольшей концентрации нагрузки.
Для приближенной оценки Кu, Kb определяют из таблиц и графиков.
В процессе вращения крутящий момент меняется с частотой
n= z W/(2p),
где z - число зубьев колеса; W - угловая частота вращения колеса.
Силы в зацеплении.
Обычно в основе расчета всех сил зацепления лежит окружная сила
Ft= 2Mкр1 /dw1 » 2Mкр1/ d1. (5- 34)
Далее рассчитываются
радиальная сила
Fr= Ft tgaw; (5-35)
нормальная сила, действующая в точке А под углом aw
Fn= Ft /cosaw. (5-36)
Если же рассматривать физический процесс, то исходной является нормальная сила, разлагающаяся на радиальную и окружную.
Поскольку наименьшая контактная выносливость имеет место в около полюсной зоне, то расчеты на прочность выполняют в полюсе зацепления П.
Контактные напряжения определяют с помощью выражения (5-32). Если учесть, что радиусы кривизны эвольвент зубьев в точке касания описывается выражениями r1= dw1sin(aw/2); r2= dw2sin(aw/2), а также, что удельная расчетная рабочая нагрузка в зоне зацепления q= FnKн/bw= Ft Kн/(bw cosaw), то получается
sН= 1,18 {EnpMкр1КН (u± 1)u-1[d2w1bwsin(2aw)]}1/2£ [sН], (5-37)
где bw - ширина зуба; [sН] - допускаемое контактное напряжение (определение его будет рассмотрено ниже). Знак “-” берется для вогнутого зацепления. В последующем будем рассматривать только эвольвентное зацепление.
Параметр u= z2/z1= dw2/ dw1 называется передаточным числом или передаточным отношением. Обычно для редуктора u> 1. В принципе передаточное число для зубчатой передачи может быть меньше нуля, меньше единицы и поэтому, в общем, оно обозначается буквой “i”. Значения расчетных напряжений одинаковы для колес и шестерен. Поэтому расчеты на прочность производятся для колеса (обычно у него меньше допускаемые напряжения).
При проектном расчете надо определить размеры передачи по заданным основным характеристикам: Мкр1; Мкр2; u.
С этой целью уравнение (5- 37) решают относительно А или d1. Другие неизвестные параметры оценивают приближенно. Так, принимают
dw1» d1; aw= a= 20°.
Затем в первом приближении могут принимать какие-либо другие параметры. Здесь принимаем, что отношение ширины колес к межосевому расстоянию равно y‘ba = bw/ A= 0,4.
Тогда коэффициент ширины шестерни y‘bd= bw/dw1= =0,5y‘ba(u+1).
С использованием таких данных далее рассчитываем межосевое расстояние
A= 0,85 (u+1){EnpMкр2KНb /([sH]2u2y‘ba)}1/3, (5-38)
где KНb- коэффициент концентрации контактной нагрузки определяем из графика, учитывающего значение y‘bd и особенностей конструкции данной передачи.
Расчетную величину А округляют по стандартному ряду.
Затем определяем ширину зуба колеса
bw= 0,4*А.
Модуль зацепления выбирается в зависимости от ширины зуба. Отношение y‘m= bw/ m выбирается из таблицы, где учитываются особенности конструкции и работы узла. Тогда
m= bw/y‘m. (5-39)
Затем по этому значению выбирается значение модуля из стандартного ряда.
При выборе модуля зацепления следует учитывать:
1. Мелкомодульные колеса с большим числом зубьев предпочтительны по условиям плавности хода передачи и экономичности.
В таком зацеплении уменьшаются потери на трение, сокращается расход материалов.
2. Крупномодульные колеса с большим объемом зуба дольше противостоят износу, могут длительно работать после начала выкрашивания, менее чувствительны к перегрузкам т неоднородности материала.
После определения модуля зацепления уточняют все остальные параметры передачи:
суммарное число зубьев
zå= 2A/m;
число зубье шестерни
z’1= zå /(u+1);
(При z’1< 17 зацепление следует выполнять со смещением. Иначе произойдет подрезание зубьев (см. рис.5.34). Подробно такой случай рассмотрен в [4]. В случае положительного смещения толщина зуба возрастает, а при отрицательном- уменьшается)
. 
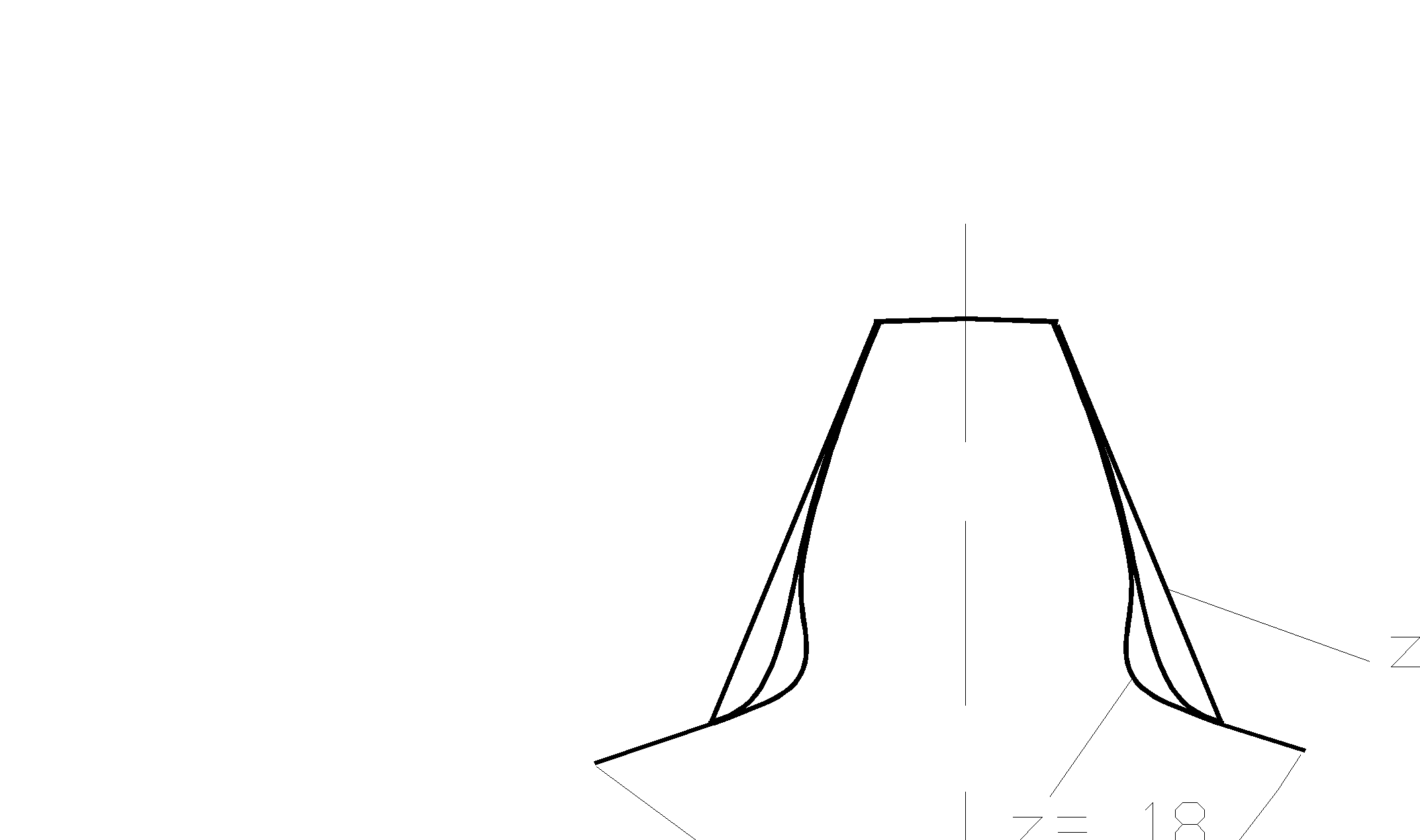
Рис. 5.34
Подрезание зубьев
число зубьев колеса
z’2 = zå - z1;
фактическое передаточное отношение
u’= z’2/z’1;
делительные диаметры шестерни и колеса
d1’= z’1m; d2= z’2 m.
Если u’ и задаваемое передаточное отношение отличаются свыше 4%, необходимо варьированием коэффициента y‘ba выбрать новые межосевое расстояние, ширину зуба, модуль и вновь рассчитать число зубьев.
Затем для выбранного m проверяем прочность зуба по контактному напряжению.
При этом определяем окружную скорость
u= pd2n2/(60*1000). м/с
По таблице [4] назначаем, например, 9-ю степень точности и определяем КНu , а с учетом выше выбранного значения KHb получим KH= KHb КНu. После этого при a= aw= 20° находим контактное напряжение между зубьями
sН= 1,18 {EnpMкр1КН (u+ 1)u-1[d2w1bwsin(2aw)]}1/2, (5-40)
которое должно быть меньше допускаемого контактного напряжения. Если разница между получившимся значением sН и допускаемым значением превышает 4%, то следует подбором bw, m выбрать параметры, удовлетворяющие данному требованию.
После этого расчета проверяется прочность зуба на изгиб.
Наибольшие напряжения образуются у корня зуба в зоне перехода эвольвенты в галтель. Из-за сложности профиля точный расчет возможен только в рамках теории упругости с применением ЭВМ. На практике такой расчет выполняется с использованием графика, иллюстрирующего связь коэффициента формы YF с числом зубьев шестерни и колеса. Далее определяются отношения [sF2]/ YF2 ; [sF1]/ YF1.
Дальнейший расчет проводим для пары, у которой это отношение меньше.
По графику, учитывающему коэффициент y‘bd, особенности конструкции пары, определяем коэффициент KFb. Затем из таблицы, устанавливающей соответствие между указанным коэффициентом, степенью точности и скоростью движения u, находим коэффициент KFu. Тогда KF= KFb KFu.
Рассчитаем окружную силу
Ft2= 2Mкр2/ d2.
Тогда напряжения изгиба в основании зуба
sF2= YF2Ft2KF/(bwm), (5-41) которое не должно превышать допустимых значений.
Дата добавления: 2015-02-23; просмотров: 1581;