Цепные передачи

1 4 3 2

а) б)

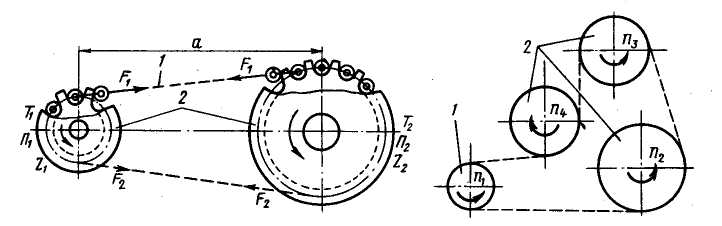
Рис. 5.75 Цепные передачи (а) с одним и (б) с несколькими выходными валами:

1- звездочка ведущая; 2- звездочка ведомая; 3- ведущая ветвь; 4- ведомая ветвь.

Принцип зацепления, а не трения, повышенная прочность стальной цепи по сравнению с ремнем позволяют передавать цепью более высокие нагрузки, но меньше, чем у зубчатых передач.

Здесь при нормальной работе нет скольжения, буксования, возможно функционирование при значительных кратковременных перегрузках. В этой передаче в принципе не нужно предварительного натяжения цепи. Угол охвата звездочки цепью по сравнению с ремнем не имеет решающего значения. Поэтому цепные передачи могут работать при меньших межосевых расстояниях а и больших i, а также передавать мощность от одного к нескольким валам (рис. 5.75,б).

Недостатки.

Поскольку цепь состоит из отдельных жестких звеньев и располагается на звездочке по многоугольнику, то это приводит к дополнительным динамическим нагрузкам, износу, шуму.

Цепные передачи применяют в сельскохозяйственном, транспортном и химическом машиностроении, станкостроении, горнорудном оборудовании и подъемно- транспортных устройствах.

Основные характеристики цепных передач.

Мощность

N= F_tu = F_tp nD₁/(60*1000)= F_t n zh_ц/(60*1000), (5-118)

где z- число зубьев звездочки; h_ц - шаг цепи; F_t - окружная сила.

Передачи обычно работают при u £ 15м/ с, n£ 500 об/мин, но есть и более быстроходные конструкции.

Передаточное отношение

i= n₁/ n₂= z₂/ z₁£ 6.

К.п.д. передачи h= 0,96…0,98.

Межосевое расстояние равно

а= (D_a1+ D_a2)/2 + (30…50), мм

где D_a1, D_a2 - наружные диаметры звездочек.

На практике

а= (30…50)h_ц. (5-119)

Длина цепи, выраженная в шагах или числом звеньев цепи определяется выражением

L_p» 2A/h_ц+ (z₁+ z₂)/2+ [(z₂- z₁)/(2p)]²h_ц/а .

По этому значению уточняют межосевое расстояние

а= 0,25 h_ц{L_p- (z₁+ z₂)/2+ [(L_p- 0,5(z₁+z₂))²- 8((z₂- z₁)/(2p))²]^1/2}. (5-120)

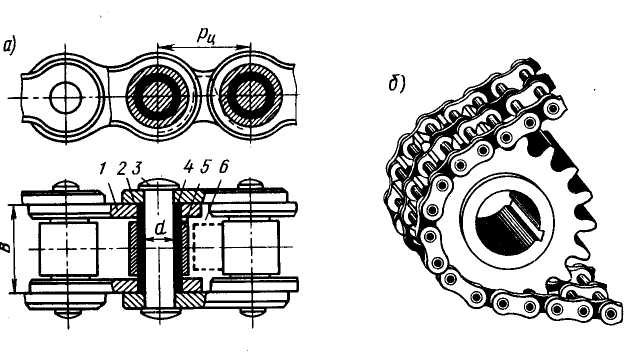
Рис. 5.76. Цепь однорядная приводная роликовая.

Передача лучше работает при небольшом провисании холостой (ведомой) ветви. Поэтому расcчетное а уменьшают на (0.2…0,4)%.

Длина цепи увеличивается по мере износа шарниров (рис.5.76,а). Для регулирования применяют специальные устройства.

Делительный диаметр звездочки определяется из соотношения

d= h_ц/ sin(p/z), (5-121)

Силовая схема в цепной передаче подобна ременной, т.е.

F_t= F₁- F₂; F_u= qu²- центробежная сила (q - масса единицы длины цепи); F₀= k_fa_в qg- сила предварительного натяжения; a_в - длина свободной (ведомой) ветви; k_f - коэффициент провисания, зависящий от расположения привода и стрелы провисания f.

Обычно F_u=0,001F_t; F₀= 0,04F_t.

Кинематика и динамика цепной передачи.

На рис. 5.77 показаны скорости движения шарниров и зубьев ведущей звездочки. В зависимости от положения ведущего шарнира составляющие скорости изменяются [4]

u₂= ucos q; u₁= usin q.

Здесь значения угла q изменяются в пределах -j/ 2£ 0 £ + j/ 2. Угол (-j/ 2) соответствует моменту входа в зацепление шарнира А, угол (+j/ 2) – шарнира В, а j= 2p/ z, где z - число зубьев звездочки. Круговая частота колебаний скоростей движения составляет

w= 2pW /j= z W.

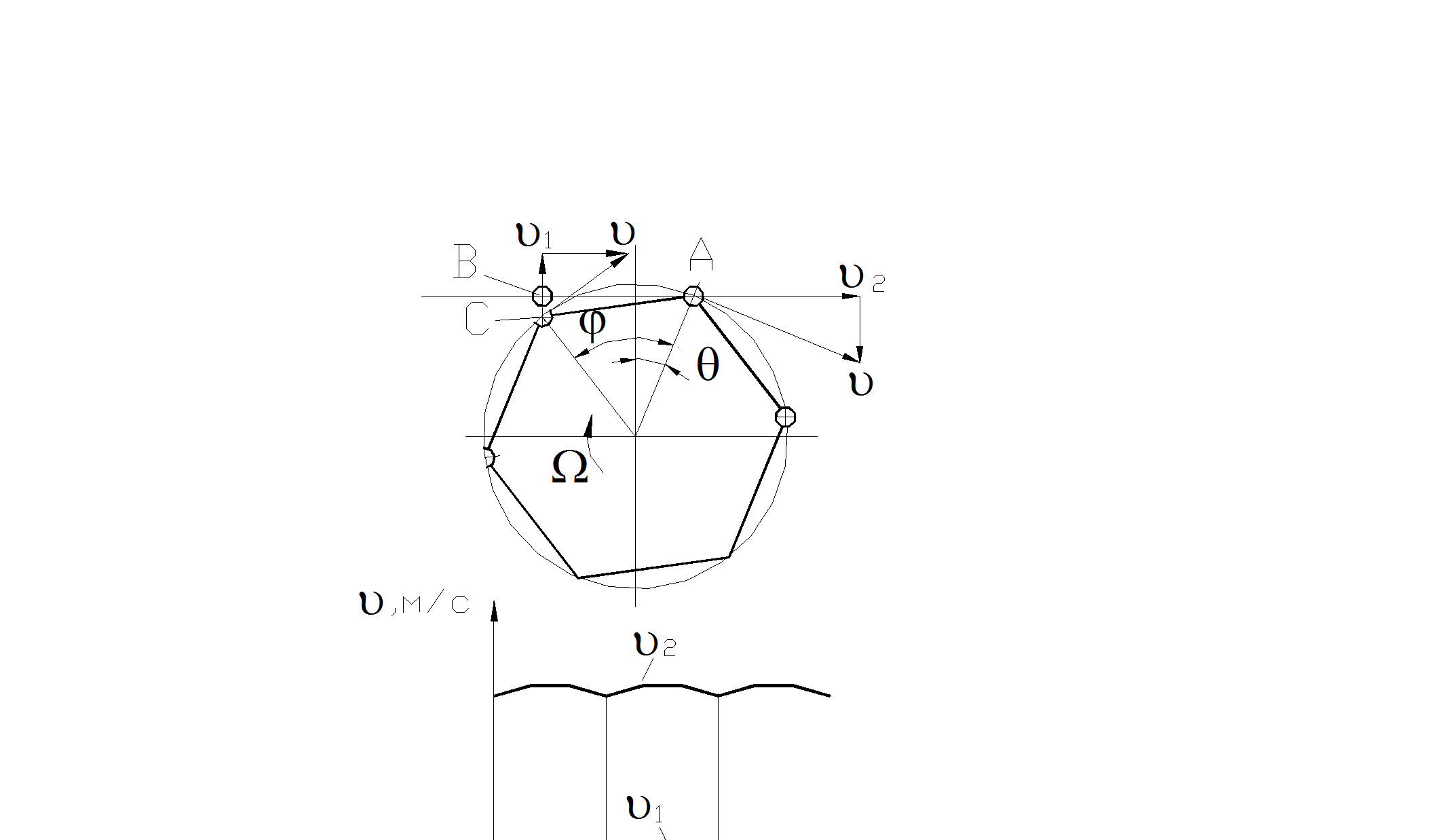
Рис. 5.77

Колебания скоростей движения деталей цепи.

Колебания скорости u₂ для ведомой звездочки приводят к колебаниям скорости движения исполнительного органа. Со скоростью u₁ связаны поперечные колебания ветвей цепи и удары шарниров цепи о зубья звездочки.

Установлено, что при отсутствии резонанса вредное влияние пульсаций скоростей значительно снижается из- за упругости, провисания и демпфирующих свойств цепи. Приближенно для оценки критической частоты вращения можно использовать формулу

n_1k= 30(F₁/q)^1/2(z₁а), [ об/мин] (5-122)

где а - межосевое расстояние в м.; F₁ -натяжение ведущей ветви, Н; q - масса 1м длины цепи, кг/м.

Энергию удара шарнира о зуб можно оценить с помощью выражения

E_k= 0,5q n²₁p_ц³sin² (360°/z₁+ g)£ [E_k],

где p_ц - шаг цепи; g - угол профиля зуба звездочки.

Последовательные удары, сопровождающиеся шумом, и являются причиной разрушения шарниров цепи и зубьев звездочки. Для ограничения вредного влияния ударов выработаны рекомендации по выбору шага цепи в зависимости от быстроходности передачи.

Все детали стандартных цепей конструируются примерно равнопрочными, что достигается сочетанием размеров деталей, материалов, термообработки ….

За основу принят расчет износносостойкости шарниров с критерием

p= F_t/(Bd)£ [p], (5-123)

где p - давление в шарнире; d, B - диаметр валика и длина (ширина) втулки.

За один пробег цепи в каждом шарнире совершается 4 поворота: 2- на ведущей; 2- на ведомой звездочках. Эти повороты вызывают износ втулок и валиков. Давление влияет на долговечность в степенной (3-й) зависимости.

Допускаемое значение относительного износа Dh_ц/h_ц ограничивается возможностью потери зацепления цепи со звездочкой и уменьшением прочности цепи. При этом цепь смещается к вершинам выступов звездочек, т.е. она располагается на новом диаметре. В таком случае возастает возможность спадания цепи. Однако чем меньше число зубьев, тем меньше вероятность этого события.

Существует оптимальное число z , когда цепь имеет масимальный срок службы с учетом прочности и способности к зацеплению. Для роликовых цепей рекомендуемое сочетание z и i, приведенное в таблице 5.7

Табл. 5.7

Выбор числа зубьев ведущей звездочки по передаточному отношению

Допускаемое давление в шарнирах определяется из соотношения

[p]= [p₀]K_э, (5-124)

где [p₀] - начальное значение допускаемого давления; K_э= K_q K_A K_H х х K_регK_сK_реж - коэффициент эксплуатации; K_q - коэффициент динамической нагрузки; K_А - коэффициент межосевого расстояния; K_Н - коэффициент передачи к горизонту; K_рег - коэффициент регули-ровки; K_с - коэффицент смазки; K_реж - коэффициент режима или продолжительности работы.

Коэффициенты выбираются из таблиц.

Расчет цепной передачи.

Дано: N= 2,8 кВт; n₁ = 150 об/мин; i= 3.

Определить: h_ц- шаг цепи; z, a.

1. Из таблицы 5.7 определяем z₁ . Для i=3- z₁ = 25.

Откуда z₂ = z₁ i= 25*3= 75.

2. Назначаем а= 40h_ц.

3. Определяем расчетную мощность, приняв по таблицам К_с= 1,3, а остальные коэффициенты равными единице.

Тогда К_э= 1,3.

Определим коэффициент числа зубьев К_z= z₀₁/ z₁= 25/25=1.

Здесь z₀₁ - стандартное число зубьев (табл. 5.7).

Определим коэффициент частоты вращения

K_n= n₀₁/ n₁= 200/150= 1,33.

Здесь n₀₁ - стандартная частота вращения (из таблиц).

По таблицам принимаем коэффициент числа рядов, учитывающий неравномерность распределения нагрузки по рядам К_ряд= 1.

Тогда расчетная мощность будет

N_p= NК_эK_zK_n= 2,8*1,3*1,33= 4,85 кВт.

4. Из таблицы для принятых n₀₁= 200 об/мин и N_p= 4,85 кВт назначаем цепь приводную роликовую ПР-19,05- 32000 с шагом 19,05 мм.

Тогда а= 40*19,05 @ 760 мм.

Из таблиц следует, что для n₁ = 150 об/мин максимальный допускаемый шаг цепи составляет 50,8 мм.

5. Определяем окружную скорость

u= z₁n₁h_ц/60000= 25*150*19,05/60= 1,2 м/с.

6. Определим длину цепи в шагах звеньев

L_p=2*760/19,05+ (25+75)/2+ (75-25)²/(2p)²*19,05/760= 131,6@ @132.

Тогда

a= (19,05/4){132- (25+75)/2+ [(132- (25+75)/2)²-8(75-25)²/(2p)²]}= =765 мм.

Учитывая рекомендации, уменьшаем а

Dа= 0,003а@ 2 мм, т.е. а= 763 мм.

7. Диаметры звездочек

d₁= 19,05/sin(p/25)= 152 мм; d₂= 19,05/sin(p/75)= 455 мм.

F_t= N/u= 2,8*10³/1,2= 2330 Н.

Сила предварительного натяжения о т массы цепи

F₀= K_faqg= 6*0,763*1,9*9,81= 87 H.

Коэффициенты K_f, q выбираются из таблиц.

Кроме роликовых цепей применяются и другие, например, тяговые пластинчатые и приводные зубчатые цепи (рис.5.78). Причем последние работают более плавно, с меньшим шумом, чем другие. Они обеспечивают высокую кинематическую точность передачи.

Технические требования к деталям цепей:

1. Пластины, втулки и ролики должны изготавливаться из холоднокатаного проката.

2. Детали цепей должны быть термически обработаны до твердостей

- пластины из нецементуемой стали- HRC 26…45;

- валики и втулки из цементуемой стали- HRC 54…65;

из нецементуемой стали- HRC 40…50

- ролики из цементуемой стали- HRC 47…55

из нецементуемой- HRC 42…50.

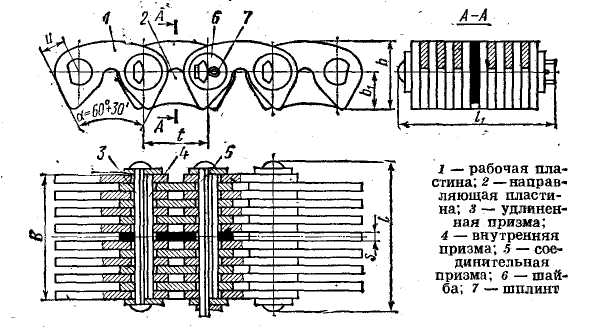
Рис. 5.78 Приводная зубчатая цепь

Валы.

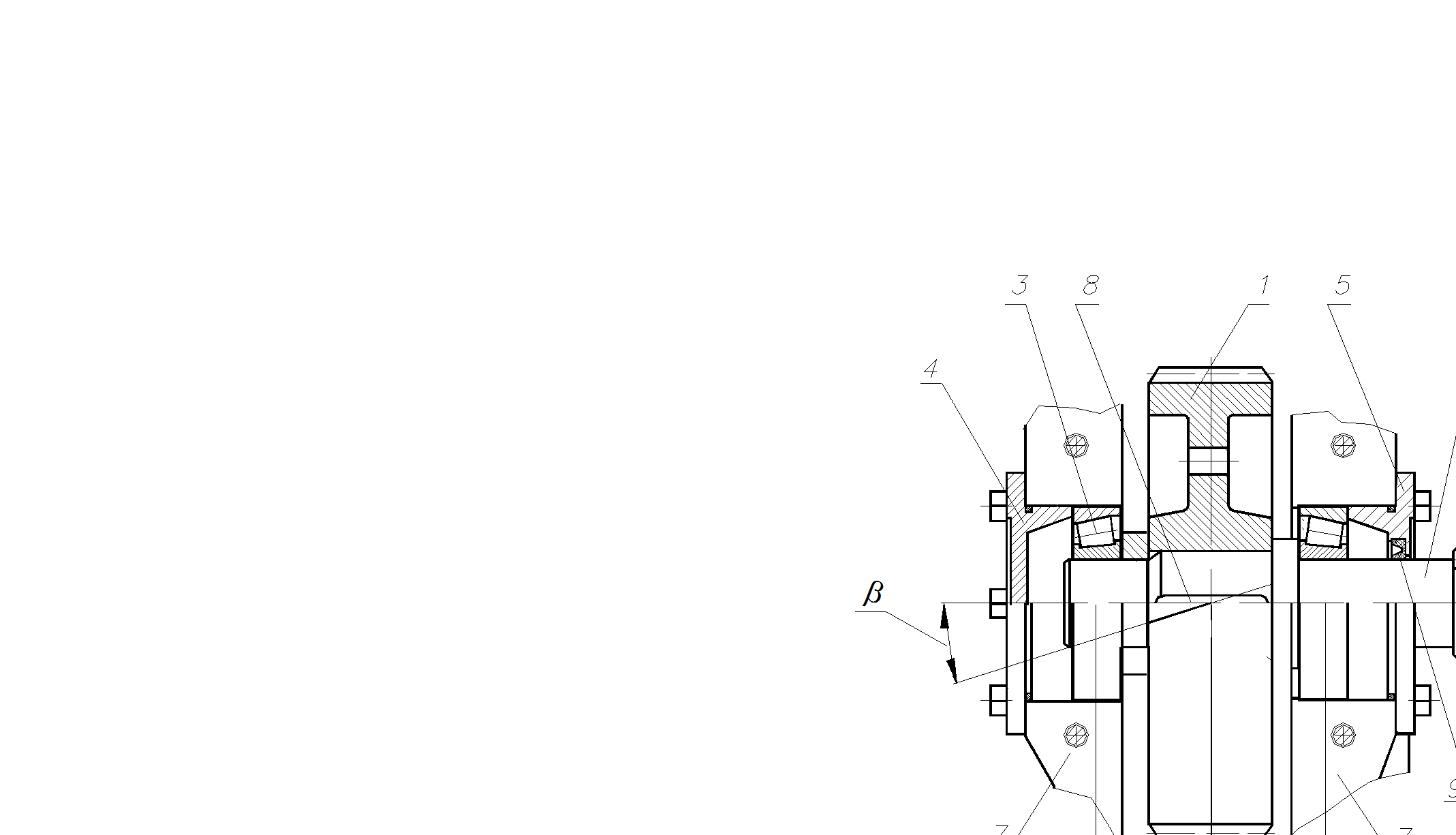
Рис. 5.79

Вал редуктора с деталями :

1-колесо зубчатое;

2- вал; 3 – подшип-ник; 4-крышка;

5- крышка; 6- звез- дочка; 7- корпус;

8- шпонка; 9-уплот-нение манжетное

.

Вал всегда вращается, а ось может быть невращающейся.

Различают валы прямые, коленчатые; гибкие.

Наиболее распространены валы прямые. Коленчатые валы применяются преимущественно в поршневых машинах; гибкие- в авиации (датчики оборотов поршневого двигателя), в зубоврачебных машинах.

Прямые валы обычно изготавливают из углеродистых и легированных сталей (Ст. 5 (0,28…0,37%C), стали 45, 40Х, 20, 20Х).

При проектном расчете обычно известны крутящий момент М_кр, мощность N, частота вращения n.

Для выполнения расчета необходимо знать конструкцию вала (места крепления нагрузки, опор и т.п.).

Порядок расчета.

1. Предварительно оценивают средний диаметр из расчета прочности на кручение

t= M_кр/W_p» M_кр/0,2d³£ [t]. (5-125)

Обычно принимают следующие значения допустимых максимальных касательных напряжений:

для трансмиссий [t]= 20…30 МПа;

для редукторов [t]= 12…15 МПа.

Кроме того, диаметр вала можно определить по диаметру вала, с которым будет выполнено соединение.

2. Разрабатывается конструкция (см. рис 5.79) с выбором подшипников.

3. Выполняют проверочный расчет и если необходимо вносят исправления в конструкцию зубчатого зацепления.

Часто диаметр вала определяется прочностью подшипников.

Проверочный расчет вала.

В расчетных схемах используют шарнирно- неподвижную, шарнирно- подвижную опоры или заделку.

Для вращающихся осей и валов защемление не допускается. Если конструкция опоры предусматривает небольшие повороты или перемещение, то этого достаточно, чтобы считать ее шарнирной или подвижной. При этом подшипники, воспринимающие осевые и радиальные нагрузки, заменяют шарнирно- неподвижными опорами, а подшипники, воспринимающие только радиальные нагрузки- шарнирно- подвижными.

Действительные нагрузки не сосредоточены, а распределены по длине ступицы. Расчетные же нагрузки полагаются сосредоточенными.

В рассматриваемом примере вал нагружен силами F_t , F_a , F_r, действующими в полюсе зацепления (рис.5.80,а) и крутящим моментом М_кр на звездочке (полумуфте).

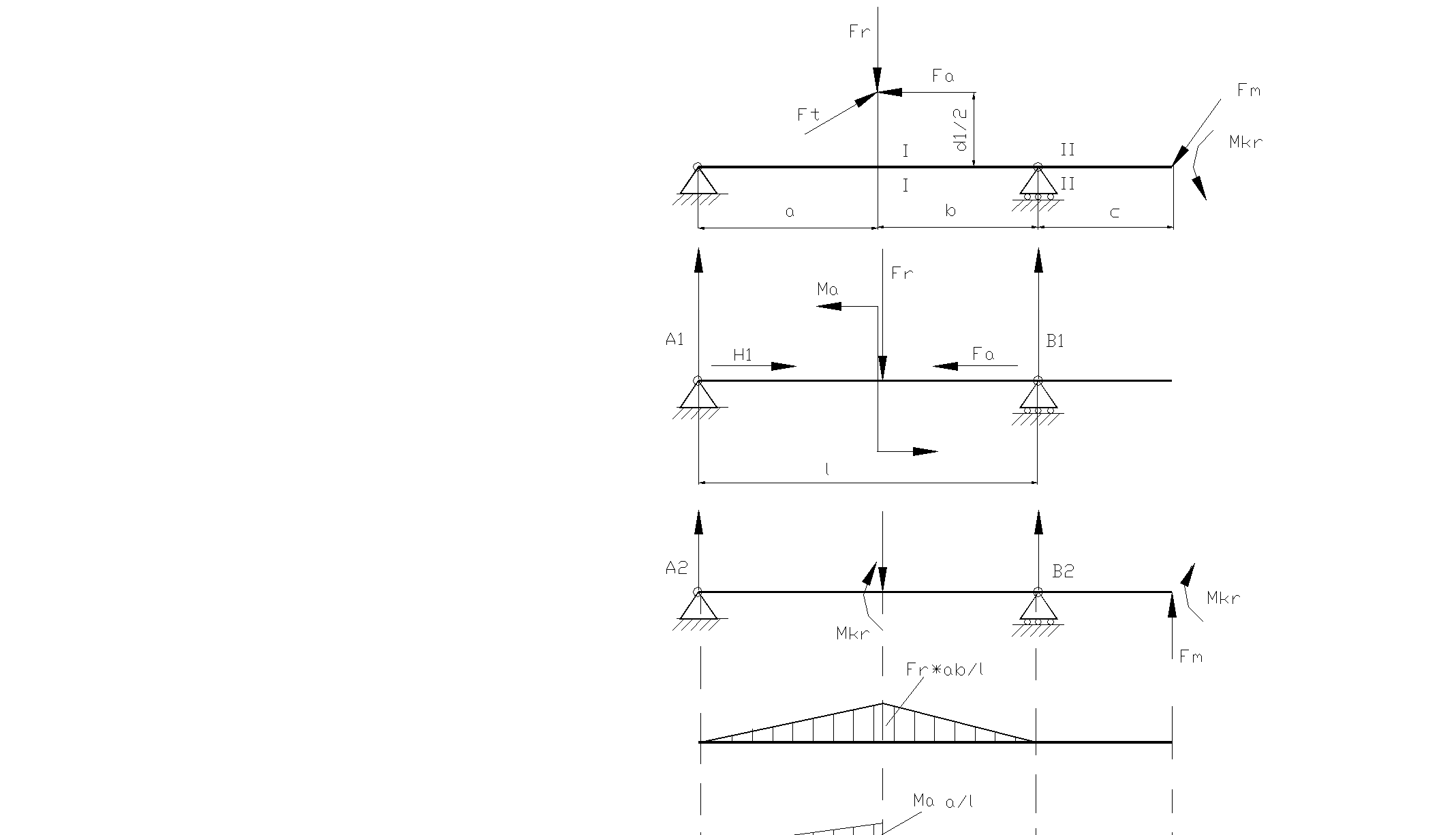
Рис.5.80. Расчет вала.

а)

б)

в)

г)

д)

Из анализа работы муфт известно, что в большинстве из них вследствие несоосности соединяемых валов возникают радиальные дополнительные силы F_m= (0,2…0,5)F_tm, где F_tm- окружная сила на муфте.

Направление силы F_tm может быть любым, т.к. зависит от случайных неточностей монтажа. Здесь мы будем считать ее направленной как на рис. 5.80,б. Для стандартных редукторов общего применения величина дополнительной радиальной силы определяется из соотношений

F_m» 125 M ^1/2_кр – для одноступенчатых редукторов;

F_m» 250 M ^1/2_кр – для многоступенчатых редукторов.

Здесь крутящий момент подставляется в Нм.

На рис. 5.80,б силы F_t, F_r, F_a- приведены к оси вала и изображены отдельно в вертикальной и горизонтальной плоскостях. При этом возникли пары сил M_a= F_ad₂/2; М_кр= F_td₂/2 (d₁- делительный диаметр колеса).

Из эпюр суммарный изгибающий момент в сечении I-I равен

M_u=(a/l) [(F_rb+ M_a)²+ (F_tb+ F_mc)²]^1/2. (5-126)

Расчет на сопротивление усталости для валов является основным.

Здесь важно установить характер нагружения, т.е. цикл. Установить действительный цикл нагружения трудно, поэтому расчет выполняется по номинальной нагрузке, а цикл принимают симметричным. Неточность компенсируют запасом прочности.

Сначала назначают опасное сечение вала, подлежащее проверке (I-I, II- II). Для опасных сечений определяют запас сопротивления усталости и сравнивают их с допускаемыми значениями. При совместном действии касательных и нормальных напряжений запас сопротивления усталости определяют из соотношения

S= S_sS_t( S²_s + S²_t)^-1/2³ [S]@ 1,5, (5-127)

S_s= s_-1 /[s_aK_s/(K_dK_F)+ y_ss_m]- запас сопротивления по изгибу;

S_t= t_-1 /[t_aK_t/(K_dK_F)+ y_tt_m ]- запас сопротивления по кручению;

s_a, t_a - амплитуды колебаний переменных составляющих циклов напряжений; s_m, t_m - постоянные составляющие.

Часто при расчете полагают s_m= 0, t_m = t_а (этот режим называется отнулевым).

Поэтому в выше приведенные формулы следует подставлять:

s_m= 0; s_а= М_и/(0,1d³); t_m = t_а= 0,5t= 0,5M_кр/(0,2d³); s_-1 = (0,4… 0,5) s_в;

t _-1 = (0,2…0,3) s_в; t_в = (0,55…0,65) s_в;

y_s= 0,05; y_t = 0 – для углеродистых мягких сталей (20, 25);

y_s= 0,1; y_t = 0,05 – для среднеуглеродистых мягких сталей (30…55);

y_s= 0,15; y_t = 0,1 – для легированных сталей; K_d, K_F масштабный фактор и фактор шероховатости (из графиков); K_s , K_t - эффективные коэффициенты концентрации нормальных и касательных напряжений (из таблиц).

Нужно знать, что с увеличением предела прочности s_в чувствительность стали к резким изменениям формы, влиянию шероховатости, размеров повышается. При разработке конструкции валов из высокопрочных сталей надо уделять особое внимание уменьшениею концентрации напряжению и шероховатости.

Сопротивление усталости можно повысить азотированием, ТВЧ, дробеструйной обработкой, обкаткой роликами … . При этом предел усталости можно увеличить на 50%. Чувствительность детали к поверхностному упрочнению уменьшается с увеличением ее размеров.

Проверку статической прочности производят для предупреждения пластических деформаций с учетом кратковременных нагрузок

s_эк= s_i= (s_u²+ 3t²)^1/2£ [s]@ 0,8s_т, (5-128)

где s_u= М_и/(0,1d³); t = M_кр/(0,2d³).

Можно использовать формулу [5]

s_из= (М_и²+ 0,45М_кр²)^1/2. (5-129)

 

Расчет на жесткость.

От прогиба вала в зубчатом соединении возникает концентрация нагрузки и при больших углах поворота может произойти защемление вала.

Допускаемые упругие перемещения зависят от конкретных требований к конструкции. В некоторых случаях оговаривается угол наклона вала.

Перемещения при изгибе определяются в общем случае методами сопромата. В сравнительно простых случаях решения табулированы (см. табл.5.8). Здесь в точках М и С сосредоточены массы колес m_M и m_C .

Угол закручивания вала постоянного диаметра определяют по формуле

j= М_крl/(GJ_p), (5-130)

где J_p= pr⁴/2= pd⁴/32- полярный момент инерции.

При ступенчатом вале, нагруженном несколькими крутящими моментами, j определяется по участкам, а затем суммируется.

Допускаемое значение угла закручивания [j] зависит от конкретного механизма. Так, в приводах следящих систем [j] составляет секунды и минуты на 1м длины; в бурении колонна труб закручивается на 2pk; в карданных валах [j] составляет несколько градусов на 1 м.

 

Таблица 5.8.

Определение параметров деформации валов

А	Б
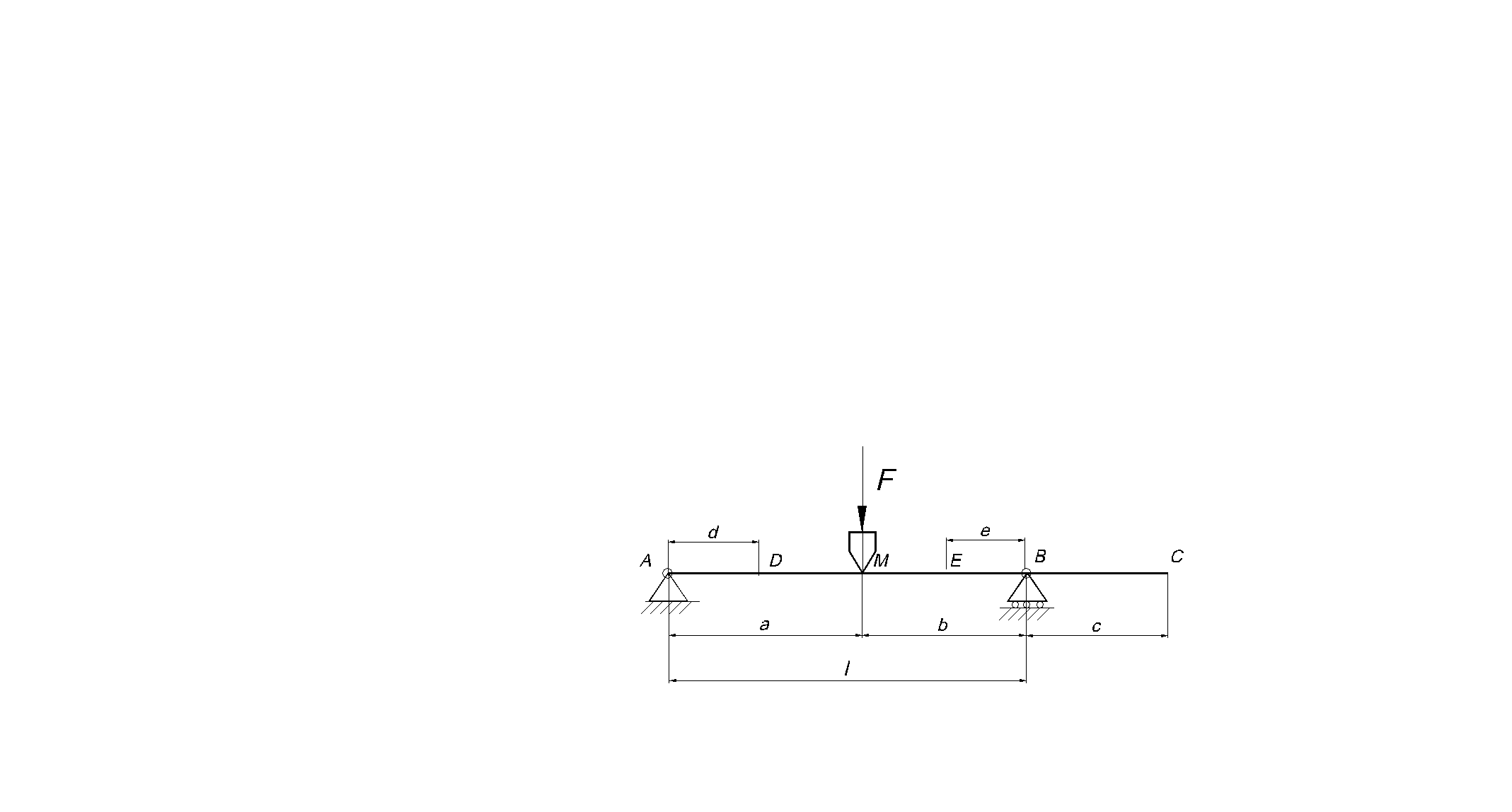qА= Fab(l+ b)/(6EJl); qB= -Fab(l+ a)/(6EJl); qC= qB; qD=Fb(l2- b2- 3d2)/(6EJl); qE= - Fa(l2- a2- 3e2)/(6EJl); qМ= Fab(b- a)/(3EJl); уМ= Fa2b2/(3EJl); yC= cqB; yD= Fbd(l2- b2- d2)/(6EJl).	qА= F1 cl/(6EJ); qB= F1 cl/(3EJ); qC= F1 c(2l+ 3c)/(6EJ); qD= F1 c(3d2- l2) /(6EJl); yC=F1c2(l+ c)/(3EJ); yD=-F1c d(l2 - d2)/(6EJl)

 

 

Анализ на изгибные колебания следует проводить по уравнениям (5- 14)…(5-21) для h=0, dy/dt=0.

Резонансную частоту для схемы действия сил А при поперечных колебаниях колеса обычно определяют из выражения w_рА=(g/y_уст)^1/2, где y_уст - прогиб вала от статической силы F=m_M g.

В случае действия сил по схеме Б уравнения движения точки С, учитывая формулу для у_с, а также выражение F₁(t)= F₁₀(t)- m_cdu_с/dt- h_cu_с, запишем в операторной форме (см. гл.3)

u_с(t)= J_c[pF₁₀(t)- h_cpu_с(1+ T_нp)]; s_B (t)= cW_z^-1[F₁₀(t)- m_cu_с(1 +T_нр)],

где W_z - геометрический момент сопротивления сечения вала; T_н=m_c/h_c; J_c=с²(l+с)/(3EJ)- коэффициент упругости.

Совместное их решение позволяет получить характеристическое уравнение D(p)= 1+ h_cJ_cp+ m_cJ_cp². Откуда следуют выражения для резонансных частот

круговой

w_рБ= {3ЕJ/[m_cc²(l+c)]}^1/2 (5-131)

и периодической n_рп= w_рБ /2p

Резонансные частоты соответствуют критической частоте вращения неуравновешенной массы

n_кр1= 30 w_р/p.. (5-132)

При этом рекомендуется выполнять условия

n£ 0,7 n_кр - для жестких валов;

n³ 1,3 n_кр - для гибких валов.

Поскольку радиальная нагрузка действует на вал с частотой n= nz/60, то появляется характеризующая зубцовые колебания критическая частота вращения n_кр2= n_рп60/ z, где z- число зубьев колеса..

Колебания нагрузки приводят к крутильным колебаниям вала.

Резонансные частоты для таких колебаний составляют

круговая

w_р3 = 1/( J_прJ_к)^1/2, (5-133)

периодическая n_рк= w_р3/2p..

Откуда третья критическая частота вращения

n_кр3= 30 w_р3/p. (5-134)

и четвертая критическая частота для зубцовых колебаний

n_кр4= 60 n_рк / z.

Во время анализа крутильных колебаний часто рекомендуют, что должно выполняться условие

J_прJ_кw²> 2,

где J_пр= mR²/2- маховой момент инерции вращающегося тела (диска); J_к= 2l/(Gpr⁴)- коэффициент упругости на кручение вала.

Однако если w< 0,5/(J_прJ_к)^1/2, то система тоже будет работоспособной.

 

Валы редукторов.

Ступенчатая форма вала позволяет свободно передвигать каждую деталь вдоль вала до ее посадочного места и просто фиксировать ее в осевом направлении. Диаметры посадочных мест назначают согласно ГОСТ 6636-69 на нормальные линейные размеры. В индивидуальном и мелкосерийном производстве заготовкой для вала обычно служит круглый прокат или цилиндрическая заготовка. В этих случаях следует избегать значительных различий в диаметрах ступеней, т.к. они приводят к обращению в стружку много металла в процессе обточки.

Скругленный галтельный переход (рис. 5.81) при небольшой высоте уступа не вызывает значительных местных напряжений. Поэтому такой переход особенно желателен в местах, где запасы прочности невелики. Если для ступени меньшего диаметра предусмотрено шлифование, то, чтобы

 

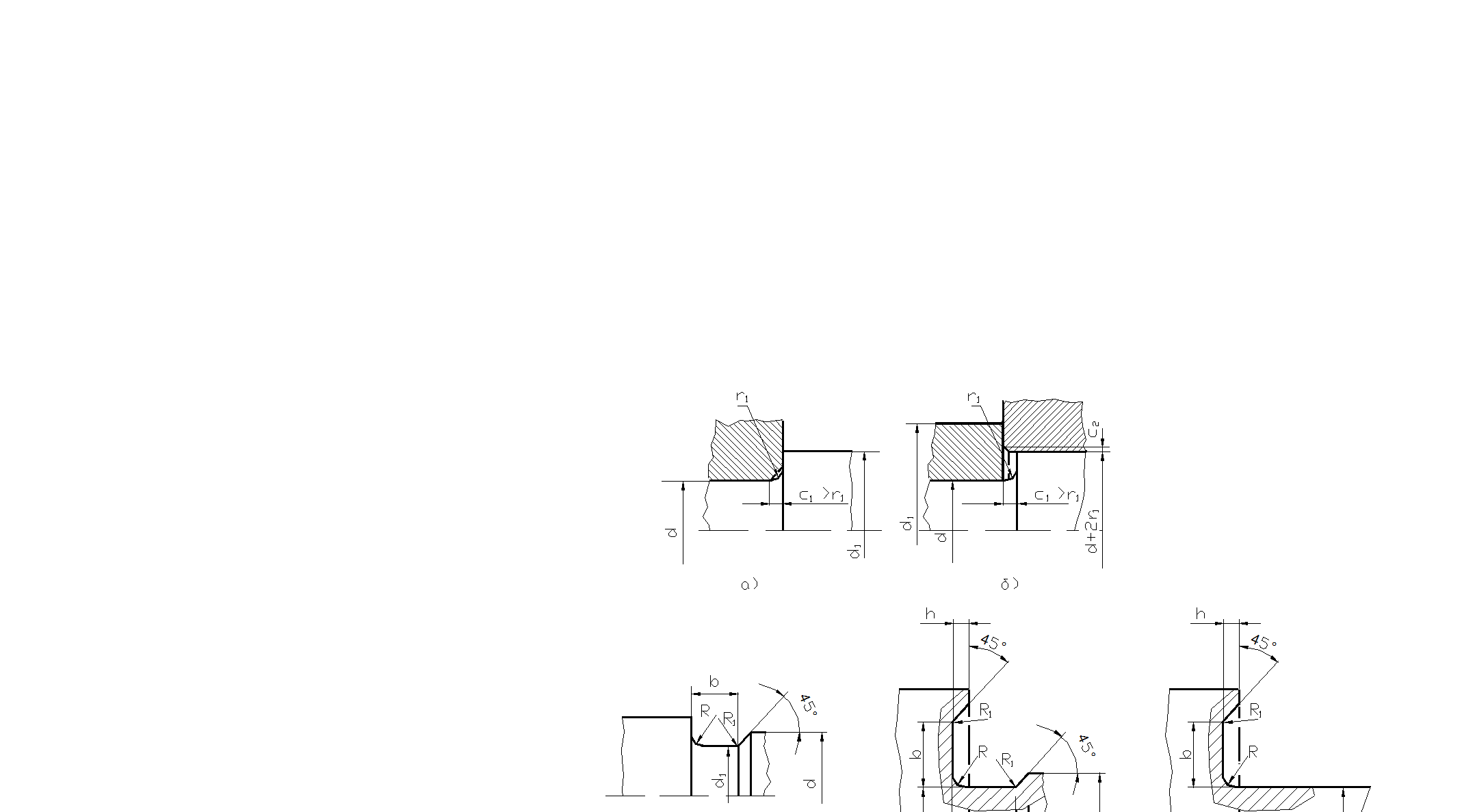
Рис.5.81

Галтельный переход и канавки для выхода круга

 

в)

получить скругленную галтель, необходимо предварительно скруглить заправкой кромку шлифовального круга.

Ширина плоской части перехода должна хорошо обеспечивать относительное положение деталей. В зависимости от осевой силы, которой нагружен уступ, и от диаметра, достаточно номинального значения этой ширины от 1,5 до 2,5 мм. Для сопряжения, показанного на рис. 5.81,а ,

d₁= d+ 2c₁+ (3…5) мм.

При сопряжении, показанном на рис. 5.81,б

d₁= d+ 2r₁+2c₂ + (3…5) мм.

Переход с канавкой, необходимый для свободного выхода шлифовального круга, выполняется по рис. 5.81,в. Такие переходы уместны, если имеются достаточные запасы прочности, поскольку канавка создает более высокие местные напряжения, чем скругленный переход.

 

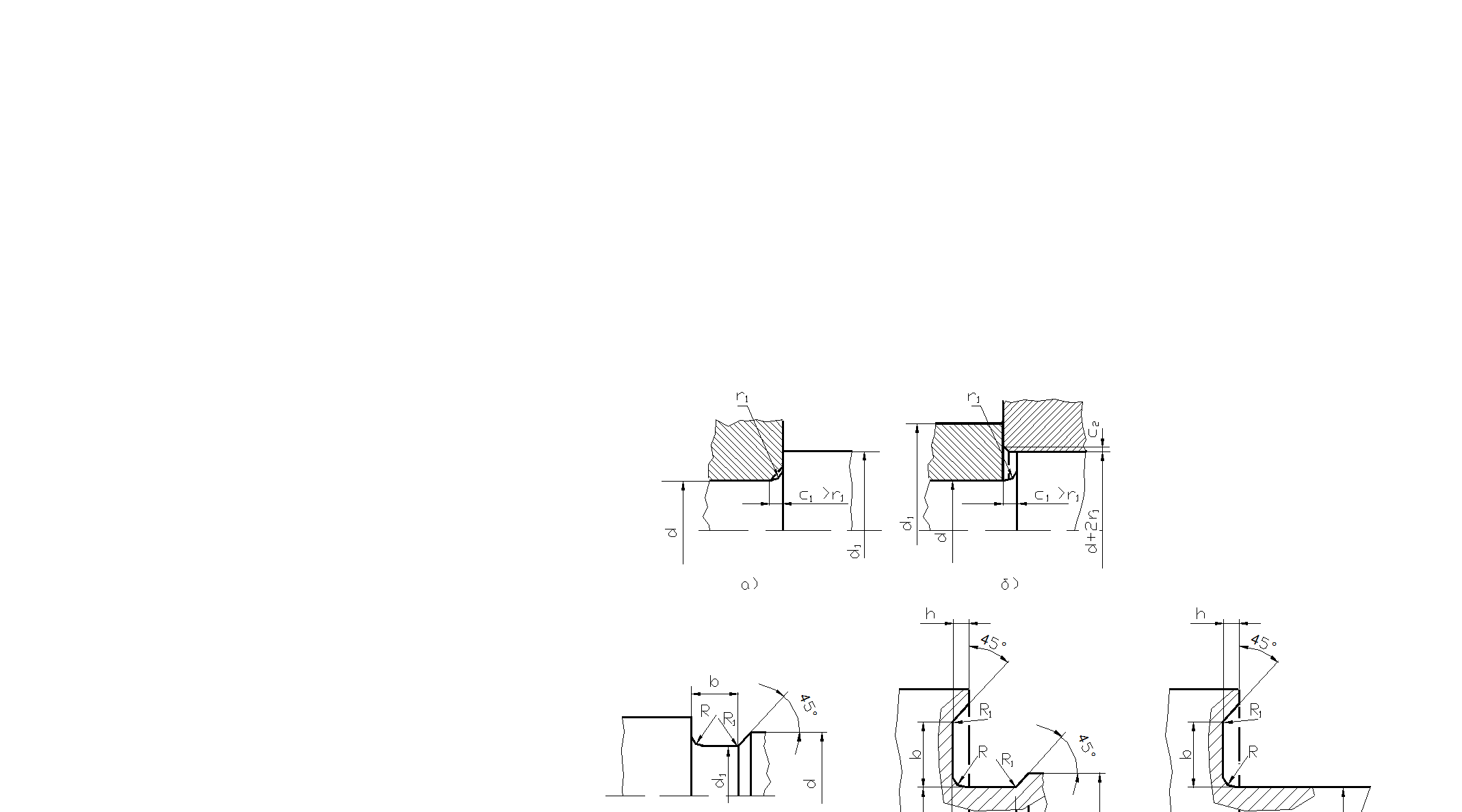
Рис.5. 82 Уступ вала у подшипника.

 

Уступ вала (заплечик), примыкающий к кольцу подшипника (рис. 5.82), должен быть выполнен так, чтобы фаска кольца подшипника свободно размещалась внутри галтельного перехода вала и высота h уступа обеспечивала правильноет положение кольца на валу. Координата r фаски кольца указывается в каталоге для каждого подшипника, а размеры перехода на валу и другие размеры приводятся в справочниках.

Присоединительные концы (хвостовики) валов делают в большинстве случаев цилиндрическими (рис. 5.83,а).

 

 

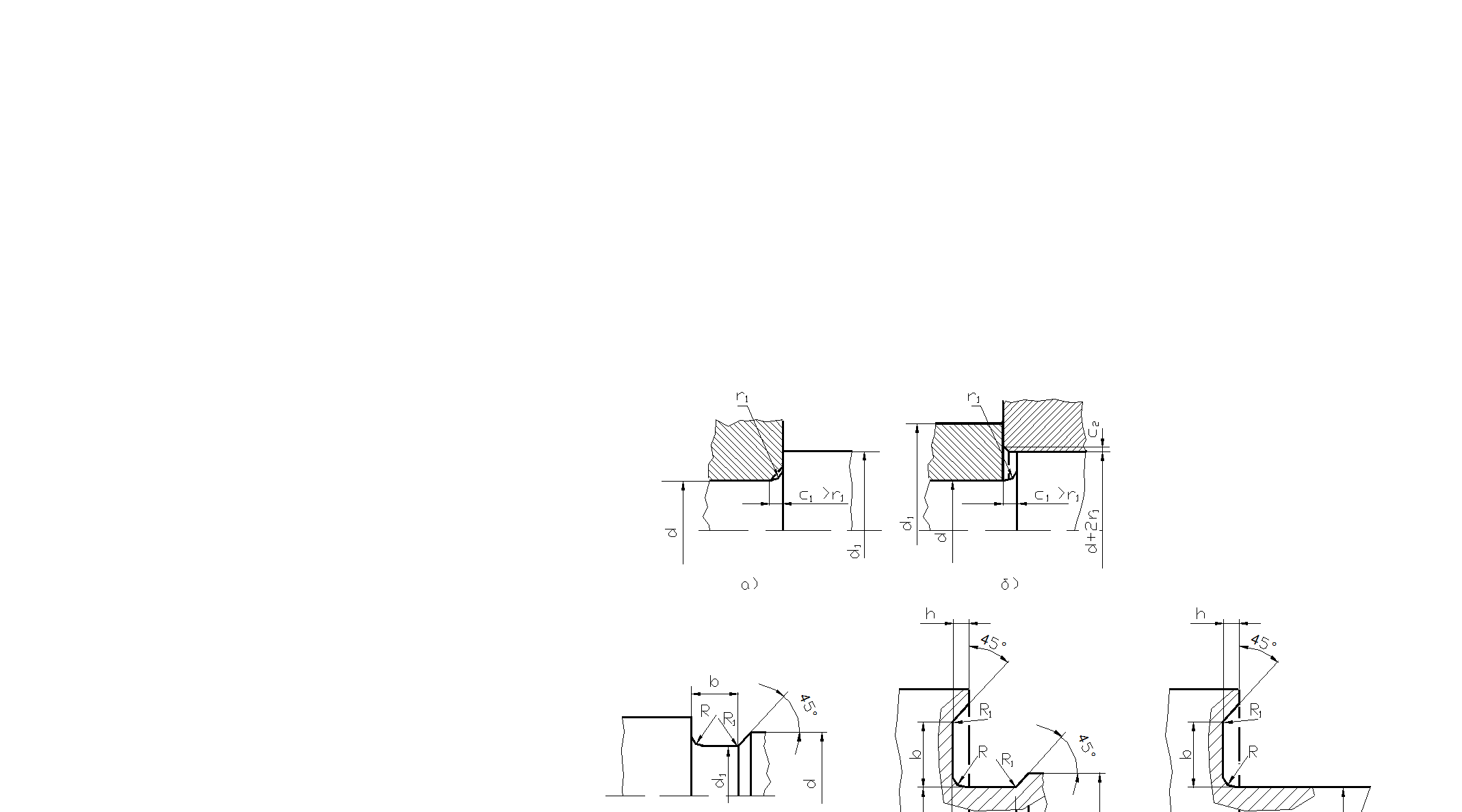
Рис. 5.83 Концы вала

 

 

Для предохранения от осевого

а) б) смещения деталей на валу исполь-

зуют упорные шайбы (рис. 5.83,б).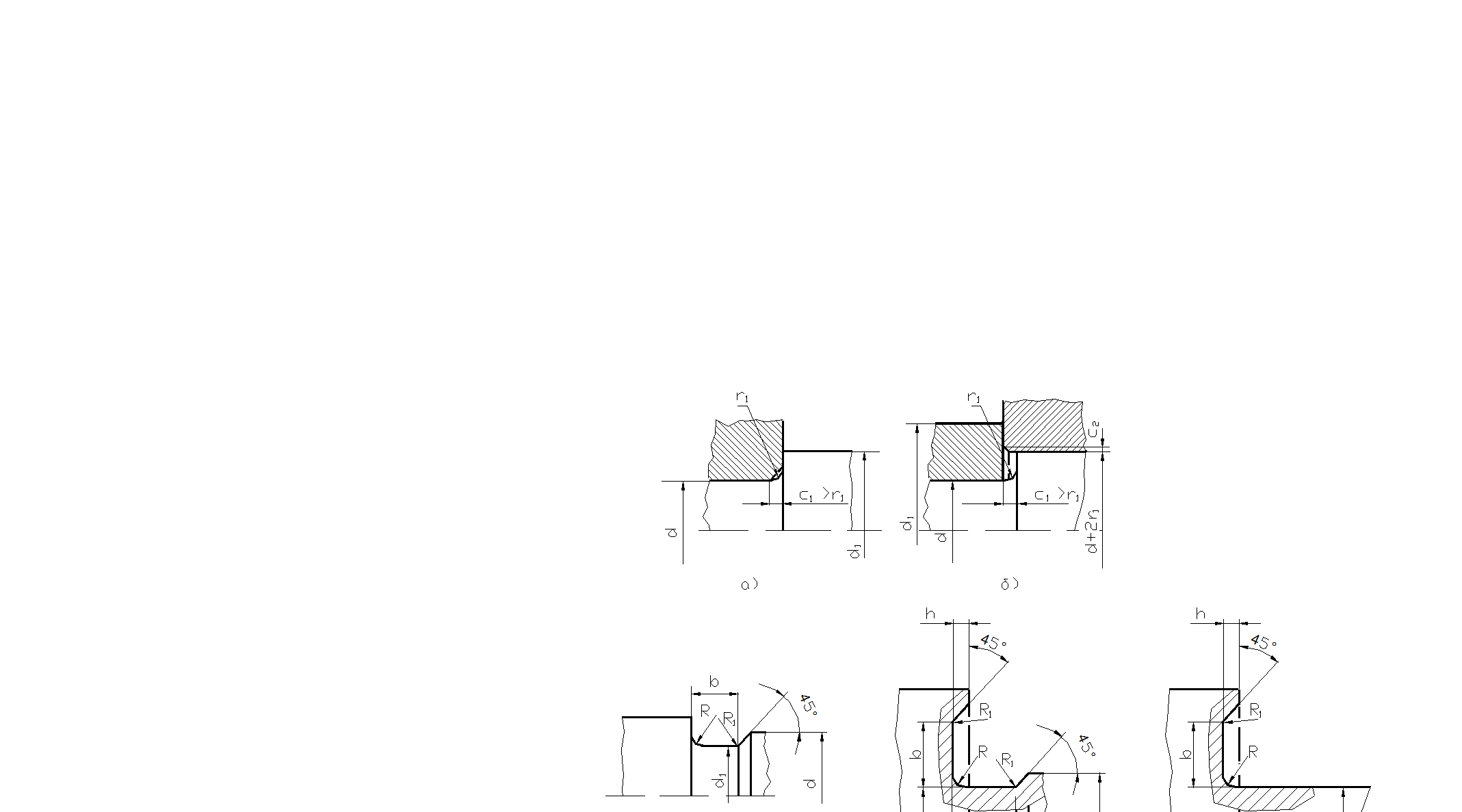

Крутящий момент через вал передается с помощью шпонок (рис. 5.83,а,б) или с помощью шпонок и конического сопряженного соединения (рис. 5.83,в).

в)

 

<60616263646566>

---

Дата добавления: 2015-02-23; просмотров: 5246;

---