Степенью свободы при отсутствии упругой связи.

Свободные колебания консервативной системы.

Система тел (материальных точек) называется консервативной, если все внешние силы, действующие на эти тела, являются стационарными и потенциальными, а все внутренние силы потенциальны. Потенциальная энергия консервативной системы не зависит явно от времени, т.е.

dW/dt= d(W_п+ W_к)/dt= 0 , (3-1)

где W_к= 0,5b(q)(dq/dt)²- кинетическая энергия; W_к= W_к(q) - потенциальная энергия; q - обобщенная координата; b(q) ³0- параметры системы тел.

В состоянии устойчивого равновесия потенциальная энергия имеет минимум, т.е. dW_п /dq|_q=qo= 0. Если это не соблюдается, то в системе тел перемещения будут иметь колебательный характер, что описывается дифференциальным уравнением

b₀ d²x/dt²+ b₀x = 0. (3-2)

где b₀x= dW_п/dx- обобщенная сила F_x, сопряженная с обобщенной координатой x= q- q_0, представляющей собою смещение из состояния устойчивого равновесия); W_п (q)= b₀x²/2; W_к(q)= 0,5b₀(dx/dt)².

Обобщенную силу в этом случае называют квазиупругой силой, а b₀ коэффициентом квазиупругой силы.

Решение уравнения (3-2) представляется синусоидой (синусоидой) (см. рис.3.2), а в аналитической форме записывается следующим образом

x= A cos (w₀t+ j₁), (3-3)

где w₀= (b₀/b₀)^1/2- собственная циклическая (круговая) частота колебаний; A ,j₁- амплитуда и начальная фаза колебаний.

При этом период колебаний будет T= 2pw₀.

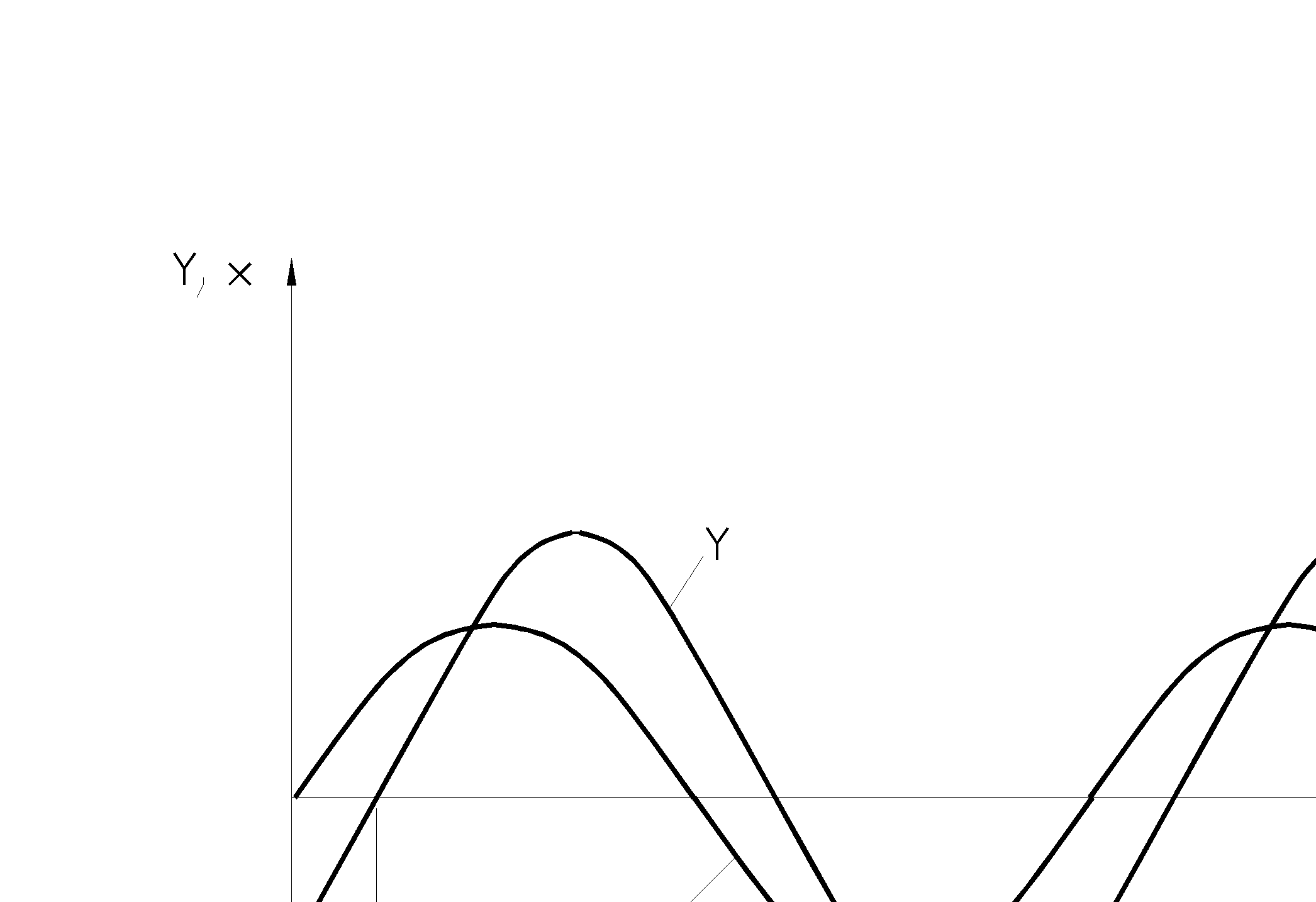
Рис.3.2

Колебательный процесс:

х- колебание из нулевой начальной

точки; у- колебание, имеющее в начальный момент смещение.

Амплитуда свободных колебаний не зависит от времени. Такие колебания называются незатухающими.

Кинетическая и потенциальная энергии при гармонических колебаниях системы являются периодическими функциями времени с периодом

T’ = pw₀. (3-4)

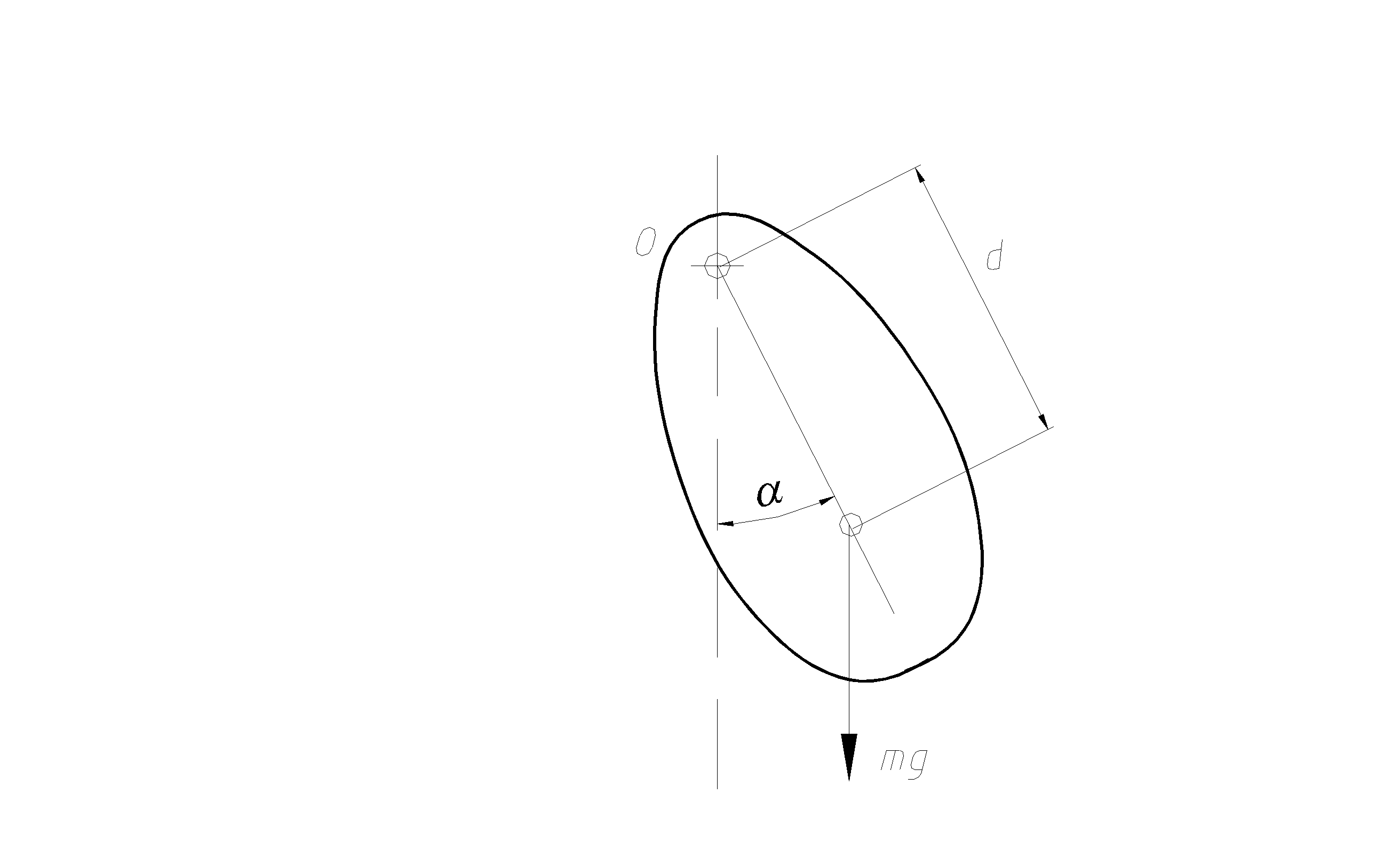Подобные колебания возникают при качании твердого тела относительно неподвижной оси, как это показано на рис. 3.3

Рис. 3.3

Физический маятник.

Здесь период колебаний равен

T= 2p[J/(mgd)]^1/2, (3-5)

где b₀= J - момент инерции тела относительно оси качания О; b₀ = mgd.

Если система обладает несколькими степенями свободы, то для анализа колебаний вводятся в рассмотрение положительно определенные квадратичные формы, приводящие к решению системы дифференциальных уравнений.

Затухающие колебания.

Это такие колебания, энергия которых уменьшается со временем. Затухание обусловлено диссипацией энергии из-за действия на систему непотенциальных сил сопротивления (трения).

Если в системе отсутствует сухое трение, а имеется лишь трение, пропорциональное скорости движения, т.е. F_тр= - rdx/dt, где r - обобщенный коэффициент трения, то для перемещений линейное дифференциальное уравнение малых затухающих колебаний записывается в форме

d²x/dt² + 2ddx/dt+ w²₀x= 0. (3-6)

или

T_и² d²x/dt² + 2x T_и dx/dt+ x= 0, (3-7)

где T_и²= 1/w²₀- постоянная времени механизма; x - коэффициент демпфирования (затухания).

Уравнения (3-6), (3-7) называют также линейными уравнениями собственных колебаний.

Если x> 1, то имеет место апериодическое затухание, при x< 1 затухание будет иметь колебательный характер.

Уравнение типа d²x/dt² + k²sin(x)= 0 является нелинейным.

При воздействии на материальную систему гармонически изменяющихся внешних сил линейное дифференциальное уравнение движения будет записываться в форме d²x/dt² + 2ddx/dt+ w²₀x= = b^-1₀ F₀cos(wt), а частота колебаний будет равна частоте вынуженных колебаний.