Рычажные и кулачковые механизмы.

Рычажные механизмы применяются в машинах, приборах и аппаратах для обеспечения требуемого движения исполнительного органа. Наиболее распространены 4-х звенные механизмы. Они могут иметь четыре шарнира (шарнирные четырехзвенники), три шарнира и одну поступательную пару или два шарнира и две поступательных пары.

На рис. 2.47,а,б показана схема аксиально- поршневого насоса и распределитель жидкости. Здесь в процессе вращения вала, прикрепленные к нему на шаровых шарнирах поршни (рис. 2.47,а) возвратно-поступательным движением в блоке цилиндров засасывают и выталкивают жидкость через окна распределителя (рис. 2.47,б). На рис.2.47,в показан кривошипно-коромысловый механизм, применяемый для преобразования качательного движения во вращательное движение.

Механизм на рис. 2.47, г подобен механизму на рис. 2.47,в, но из-за нетехнологичности его заменяют кривошипно-ползунным нецентральным механизмом (рис. 2.47,д). При десаксаже e= 0 он превращается кривошипно-ползунный центральный механизм (рис. 2.47,е). Такие механизмы широко применяются в поршневых двигателях, где 1- кривошип, 2- шатун, а ползуны 3 называются поршнями.

На рис. 2.47,ж показана схема кривошипного механизма с качающимся поршнем, применяемого в судовых двигателях.

На рис. 2.47,з показан кривошипный механизм с качающейся кулисой. Такие механизмы применяются в станках.

Применяются также синусные механизмы (рис. 2.47,и).

Существуют и другие кривошипные механизмы.

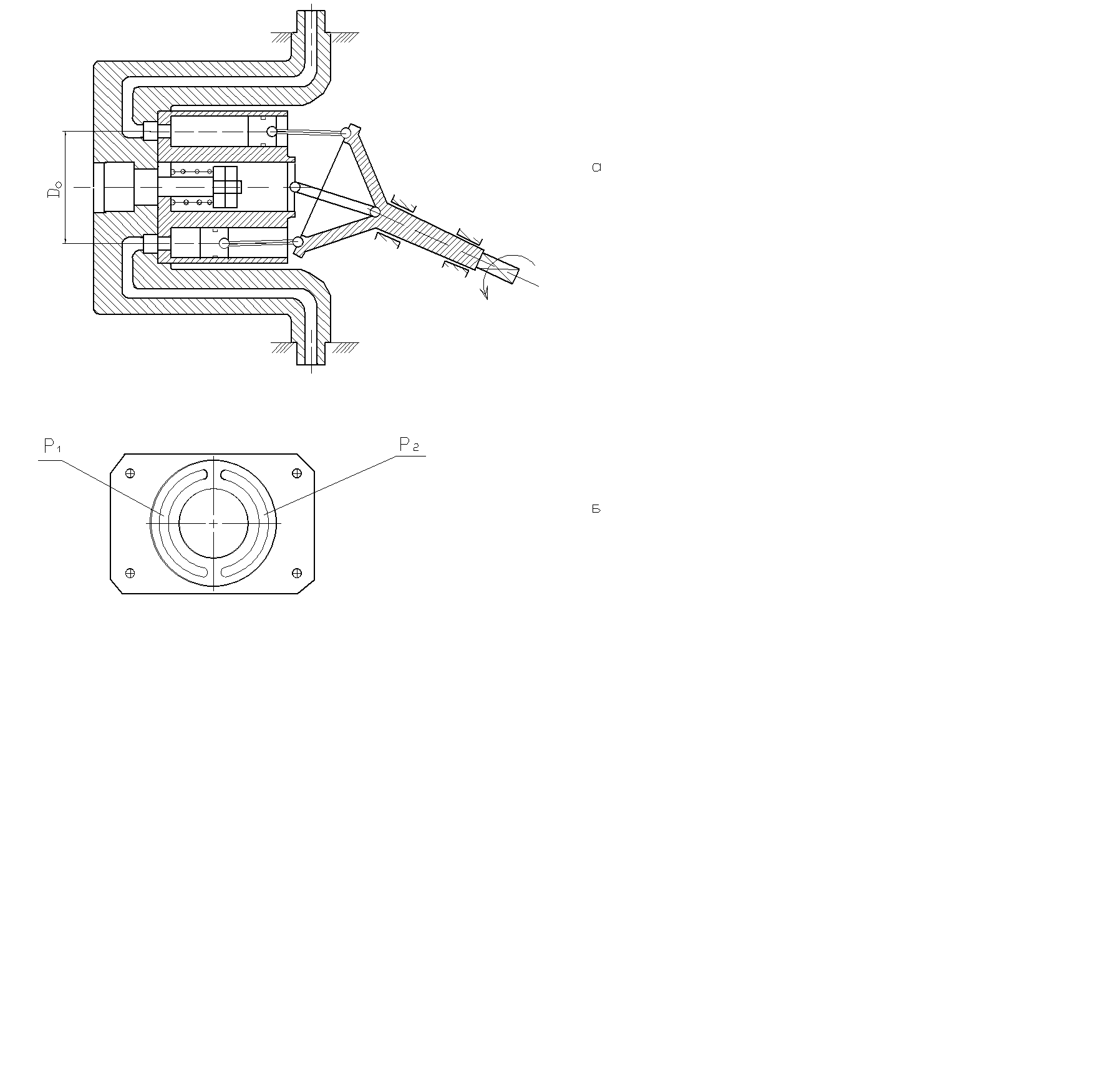
Р₂

Р₁ б)

а)

в)

Рис. 2.47. Кинематические схемы рычажных механизмов

Рассмотрим более подробно кривошипно-ползунный механизм (рис.2.47,е). Для анализа законов движения обычно применяют графический метод, включающий построение планов скоростей и ускорений.

Положение звена, из которого начинается отсчет его движения

в одном направлении, называется начальным или крайним. Положение, в котором кривошип 1 и шатун 2 располагаются на одной прямой, называется мертвым.

Метод основан на графическом решении векторных уравнений движения.

Вначале должны быть заданы: кинематическая схема; закон движения ведущего звена.

Построим план скоростей (рис. 2.48).

Пусть известны: W₁, e₁ – угловые скорость вращения и ускорение кривошипа.

1. Определяем линейную скорость движения точки А кривошипа

u_А= W₁l_OA.

Вектор скорости перпендикулярен ОА. Выбираем масштаб m_u. Откладываем из полюса Р_u отрезок Р_u а*m_u = u_А.

2. Проводим из Р_u направление скорости перемещения точки В.

3. Из точки а плана скоростей перпендикулярно ВА проводим линию в направлении скорости движения точки А шатуна.

4. Пересечение линий u_А и u_В дают скорость перемещения точки В

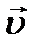_В= m_u Р_ub; )_ВА= m_u ab (2-191)

Построим далее план ускорений.

Результрующее укорение складывается из геометрических сумм нормальных и тангециальных составляющих.

1. Определяем для точки А кривошипа нормальное ускорение

aⁿ_A= l_OAW₁². (2-192)

2. Тангенциальное ускорение точки А

a^t_A= l_OAe₁. (2-193)

Вектор aⁿ_A направлен вдоль ОА к точке О, а вектор a^t_A перпендикулярен ОА.

Проведем aⁿ_A из полюса Р_а, а a^t_A из точки а’, предварительно выбрав масштаб m_а.

Тогда ускорение точки А будет

a_A= m_а Р_Ab. (2-194)

Ускорение точки В найдем из уравнения

а_В = а_А + а_ВА= а_А + aⁿ_ВА + a^t_ВА. (2-195)

Рис. 2.48

Построение планов скоростей и ускорений в кривошипно-

ползунном механизме:

а)- кривошипно-ползунный меанизм;

б) план скоростей;

в) план ускорений;

г) график изменения скорости;

д) график изменения ускорения.

Оно направлено, как следет из чертежа, вдоль ВО. Вектор aⁿ_ВА направлен по АВ к центру вращения А и откладывается из точки а плана

aⁿ_ВА= u²_ВА/ l_AB.

3.Тангенциальная составляющая a^t_ВА проходит перпенди-кулярно aⁿ_ВА.

Пересечение aⁿ_ВА с направлением ВО дает ускорение точки В

a_B= m_а Р_ab.

Если построить планы скоростей и ускорений для разных значений j, то получим графики, показанные на рис.2.48,г,д.

Отметим, что график изменения ускорения можно получить из графика изменения скорости графичеким дифференцированием.

Зная ускорение и приведенные массы, можно рассчитать силы инерции

F_u= - m_na; M_u= - J_ne,. (2-196)

а затем и реакции.

Другой разновидностью рычажных механизмов являются кулачковые механизмы (рис.2.49).

Они классифицируются

- по характеру движения (пространственные, плоские, поступательные, вращательные, качающиеся);

- по взаимному расположению кулачка и толкателя;

- по типу замыкания.

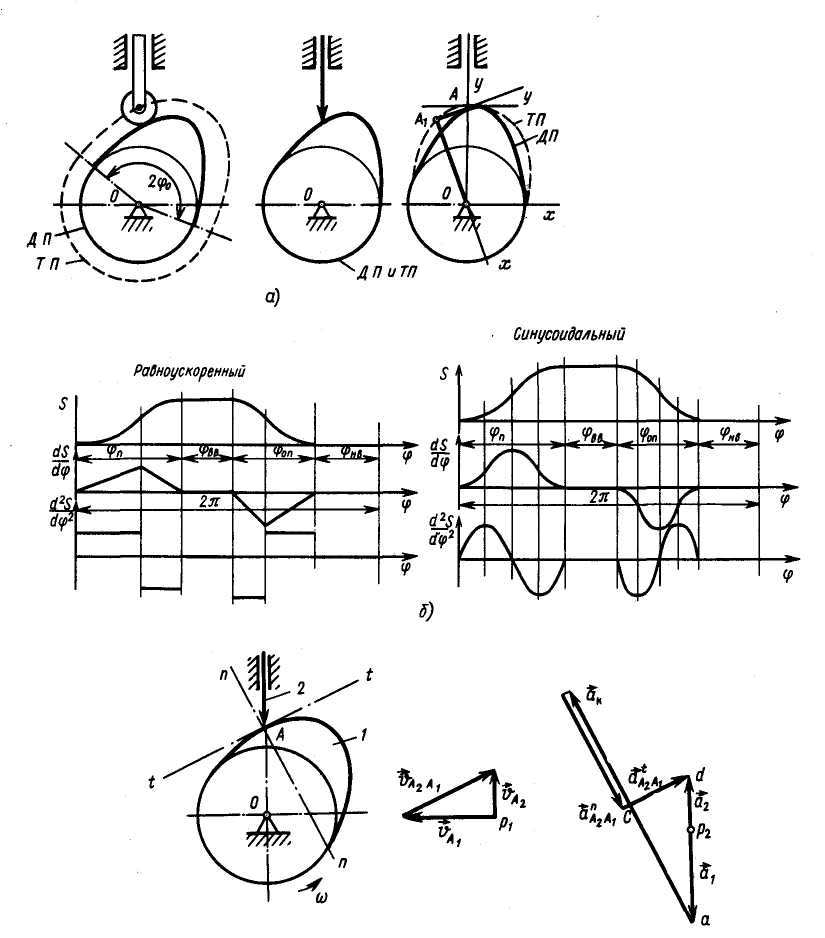
Рис. 2.49. Схема и законы движения в кулачковом механизме.

Для анализа должны быть заданы:

кинематическая схема; профиль кулачка; закон движения ведущего звена.

Анализ выполняют графическим или аналитическим методом. Строят планы скоростей, ускорений. В зависимости от профиля кулачка могут быть следующие законы движения: равноускоренный, синусоидальный .