Колебания в системе при наличии упругой связи.

В технике применяется много механизмов, где некоторая движущаяся масса имеет упругую связь с относительно неподвижной деталью (точкой). Такая связь выполняется с помощью стержня, трубы, пружины и т.п. В этом случае колебания в системе осуществляются под действием упругих сил. Тогда коэффициент b₀ в уравнениях (3-2), (3-6), (3-7) будет коэффициентом упругой силы.

Однако при этом в системе появляется еще одна переменная (напряжение в связывающем элементе), которая оказывает влияние на параметры движения, обычно нелинейного характера, и на работоспособность механизма.

Колебания в таких системах целесообразно исследовать несколько иначе.

В соответствии с теорией упругости связь линейных и угловых ускорений движения элементарных частей прямых стержней обычно описывают дифференциальными уравнениями в частных производных

¶ ²u / ¶ t ²= (E/r)¶ ²u /¶ x², (3-8)

¶ ²j / ¶ t ²= (G /r)¶ ²j /¶ x². (3-9)

где u, j - соответственно, продольное и угловое перемещения вдоль оси.

Используя уравнения количества движения (импульса) (2-23) и момента количества движения (2-31) в дифференциальной форме и совместно с (3-8), (3-9) преобразуя их, можно получить систему двух дифференциальных уравнений для каждого вида движения

для продольных колебаний

r ¶ u / ¶ t= - ¶ s /¶ x, (3-10)

E^-1(¶s / ¶ t) = - ¶ u /¶ x. (3-11)

для крутильных колебаний

r_or ¶ W / ¶ t=- ¶ t / ¶ x. (3-12)

(rG)^-1¶ t /¶ t= - ¶W / ¶ x, (3-13)

где u, W - продольная и угловая скорость; r_o - радиус сечения стержня; t - максимальные касательные напряжения.

Эти уравнения в ряде случаев, например для коротких стержней, могут быть записаны с помощью обыкновенных производных

r d u / d t= - d s /d x, (3-14)

E^-1(ds / d t) = - d u /d x. (3-15)

r_or d W / d t=- d t / d x. (3-16)

(rG)^-1d t /d t= - dW / d x. (3-17)

Рассмотрим теперь колебания в механизме, содержащем движитель (продольный или крутильный), через стержень, перемещающий исполнительный орган, имеющий инерцию, и на который действует сила трения (рис. 3.4). Причем колебания движения исполнительного органа не влияют на движитель. Используя уравнения (3-14)…(3-17) и учитывая граничные условия [6], [7], получим следующую систему уравнений

для продольного перемещения

s(t) f(1-с) = F₀ (t)+ hu₂ (t)+ mрu₂ (3-18)

u₁(t)(1-c)- J_п0 pF₀(t)= u₂(t)(1-c+ hJ_п0 p+ mJ_п0 p²), (3-19)

для крутильных колебаний

t (t)W_p =М_с0 (t)+ h_кW₂(t)+ J рW_2,. (3-20)

W₁(t)- J_к0 pM_c0(t)= W₂(t)(1+h_кJ_к0 р+ JJ_к0 p²), (3-21)

для поперечных колебаний массы на консольно закрепленной балке

- J _и p F(t) + u₀(t) = u_l(t)(1+J _иh_пк p+ J _иmp²), (3-22)

Рис.3.4 Стержень с массой на конце.

где J_к= l W_p^-1(rG)^-1- коэффициент крутильной упругости; J_п0= l Е^{-1 f -1}- коэффициент продольной упругости механической магистрали; J _и= = l³(3E J_z)^-1=D y/[F₀+mg] - изгибная упругость балки; D y,(F₀+mg)- прогиб и поперечная сила; с - коэффициент потерь на трение,

пропорциональное напряжению; h, h_к- коэффициенты потерь на трение, пропорциональное скорости движения; m, J - масса и маховой момент инерции исполнительного органа; f, W_p, W_z – площадь, момент сопротивления сечения на кручение и момент сопротивления сечения стержня на изгиб; u₁, W₁ - продольная и угловая скорости движения ведущего конца стержня; u₂, W₂ - про-дольная и угловая скорости движенияисполнительного органа; F₀, М_с0 - сила и момент сопротивления движению исполнительного органа; рº d/ dt.

На основании уравнений (3-18), (3-19) процесс передачи мощности от движителя к исполнительному органу можно представить в виде структурной схемы (рис.3.5)

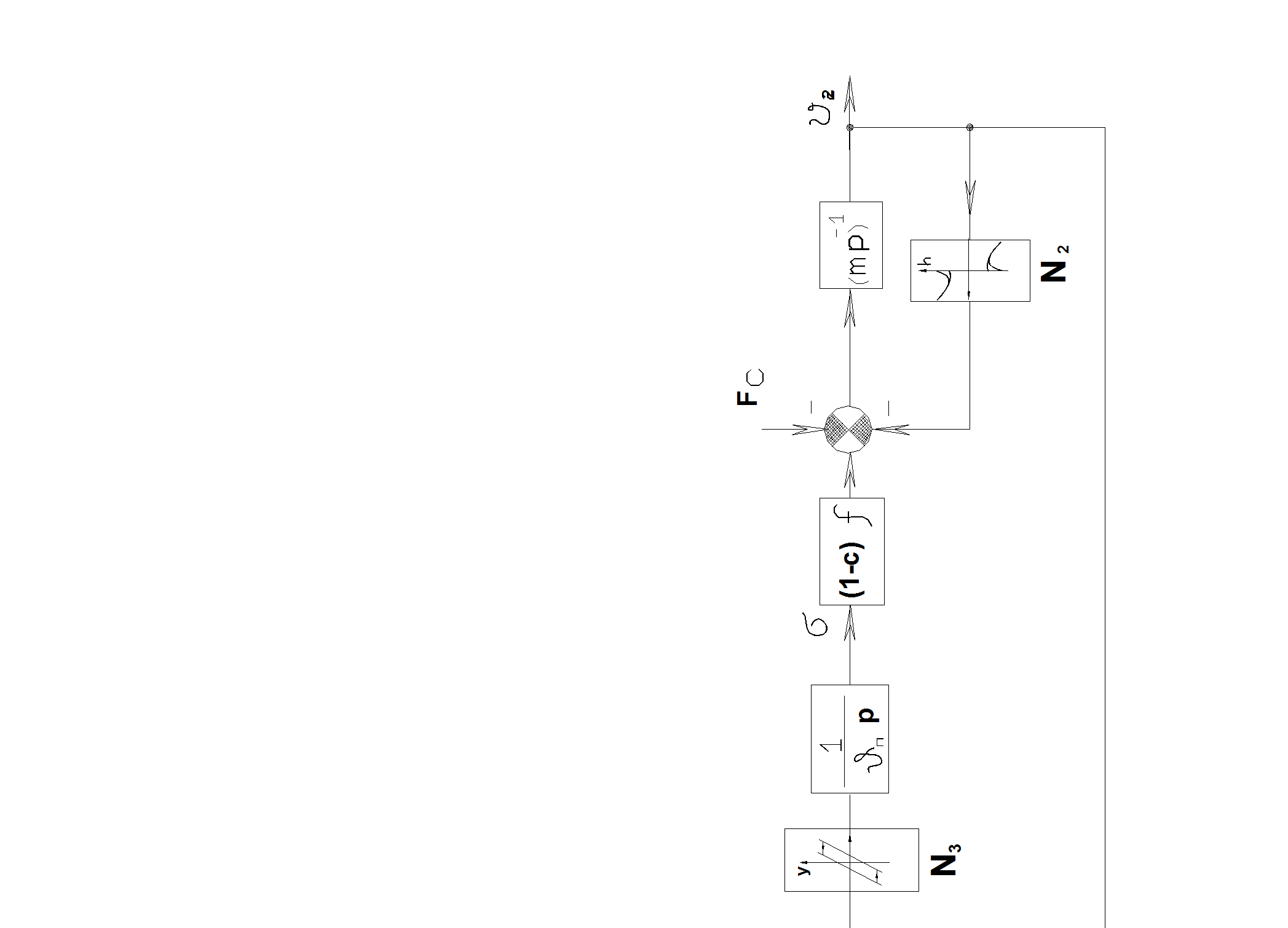
Рис. 3.5.

Структурная схема передачи мощности

Здесь буквой N₂ обозначено свойство коэффициента трения, действующего на перемещаемую массу, изменяться в зависимости от скорости ее движения; N₃ - наличие гистерезисных потерь. Буквой N₁ обозначено свойство модуля упругости становится равным нулю при деформациях, когда напряжения превышают предел текучести. Это следует из диаграммы растяжения металлов.

Подобное структурное представление процессов возможно также для крутильных, поперечных колебаний.

Заметим, что в рассмотренных примерах передача мощности происходит через металлические (стальные) детали. Если же между движителем и исполнительным органом окажется деталь из материалов с уменьшенным модулем упругости (резины, алюминия, пластика и т.п.), то приведенное значение коэффициента упругости окажется больше, нередко значительно больше.

Уравнения (3-20), (3-22), (3-23) могут быть приведены к виду

u₁(t) - k_fJ_п0 pF₀(t)= u₂(t)(1+ 2z_п Т_ип р+ Т_ип²р²), (3-23)

W₁(t)- J_к0 pM_c0(t)= W₂(t) (1+2z_к Т_ик р+ Т_ик ²р²), (3-24)

где

Т_ип= (mJ_п0 k_f )^1/2; Т_ик ²= (JJ_к0]^1/2 - постоянные времени;

z_п =0,5 hJ_п0 k_f Т_ип^-1; z_к =0,5 hJ_к0 Т_ик^-1 ;коэффициенты(3-25)

демпфирования;

k_f = (1- с )^-1.

Из этих выражений видно, что с увеличением коэффициента упругости (J_п0,J_к0) коэффициент демпфирования(z_п, z_к) также возрастает. При этом увеличивается и постоянная времени механизма (Т_ип, Т_ик) , что означает уменьшение резонансной частоты w_р= 1/Т_и. Такое изменение динамических параметров часто снижает нежелательные вибрации, но при некоторых условиях может привести к автоколебаниям пониженной частоты.