Механических систем.
Выше показано, что динамика сравнительно простых механизмов с короткими магистралями может быть описана обыкновенными дифференциальными уравнениями с постоянными коэффициентами. Однако даже при таком упрощенном представлении процессов решение оказывается не совсем простым. Причем оно дает избыточную информацию, такую, как закономерность изменения форм колебаний. Хотя зачастую для инженера достаточно знать, устойчива или нет данная механическая система, и какой может быть амплитуда колебаний скорости движения или напряжений. Подобные задачи удобней решать иным способом, например, с помощью ингегрального преобразований по Лапласу
F(s)= 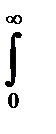 e-stf(t)dt, (3-38)
e-stf(t)dt, (3-38)
где f(t)- действительная функция, называемая оригиналом; t- время; s= s+ jw – комплексная переменная; F(s) - изображение функции f(t) на комплексной плоскости.
Часто принимают s= jw.
Рассмотрим основные особенности этого способа [7].
Преобразование имеет следующие основные свойства:
1. Умножение аргумента оригинала или изображения на некоторое число приводит к делению изображения или оригинала и их аргумента на это же число
f(at)® (1/a)F(s/a); F(as)®(1/a)f(t/a). (3-39)
Здесь под аргументом понимается соответственно t- время и s.
2. Изображение суммы конечного числа оригиналов равно сумме их изображений
[f(t)+ j(t)]® [F(s)+ j(s)]. (3-40)
3. Изображение произведения оригинала на постоянную величину равно произведению изображения на эту постоянную
af(t)® aF(s). (3-41)
4. Произведение двух изображений является изображением и равносильно свертыванию оригиналов
F(s)G(s) ® 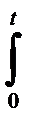 f(t)g(t-t)dt. (3-42)
f(t)g(t-t)dt. (3-42)
Интеграл в правой части называется сверткой.
5. Изображение производных оригиналов находится из соотношения
f(n)(t) ® snF(s) - f(t=+0)sn-1- f ’(t=+0)sn-2…
... f (n-2)(t=+0)s - f (n-1)(t=+0), (3-43)
где f (n)(t) - производная n-го порядка от f(t) по t; f(t=+0), f ’(t=+0),… f (n-1)(t=+0)- предельные значения, к которым стремятся функция- оригинал и ее производные, когда t стремится к нулю справа. Эти значения называются правосторонними начальными условиями.
При нулевых правосторонних начальных условиях
f(t=+0)= f ’(t=+0)=…f (n-2)(t=+0)= f (n-1)(t=+0)= 0
дифференцирование сводится к соотношению
f (n)(t) ® snF(s). (3-44)
6. Интегрирование оригинала от нуля до переменной t соответствует в пространстве изображений делению изображения на s
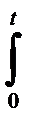 f(t) dt ® (1/s)F(s). (3-45)
f(t) dt ® (1/s)F(s). (3-45)
Для ряда случаев, разработаны таблицы перехода от оригиналов к изображениям и наоборот, приведенные в табл. 3.1.
Пусть движение в какой- либо системе описывается дифференциальным уравнением с постоянными коэффициентами
andny/dtn+ an-1dn-1y/dtn-1+…+ a1dy/dt+ a0 y(t)=
=bm dmx/dtm+ bm-1dm-1x/dtm-1+…+ b1dx/dt+ b0x(t) . (3-46)
Проведем преобразование уравнения (3-57) по Лапласу при нулевых начальных условиях, используя свойства 2,3,5
( ansn + an-1sn-1+…+ a1s + a0) Y(s)=
=(bm sm + bm-1 sm-1+…+ b1s + b0 )X(s) . (3-47)
Если y- выходная переменная, а х- входная, то отношение
bm sm + bm-1 sm-1+…+ b1s + b0
W(s)= Y(s)/X(s)= (3-48)
ansn + an-1sn-1+…+ a1s + a0,
называется передаточной функцией.
Введем оператор pºd/dt и перепишем уравнение (3-48)
bm p m + bm-1 p m-1+…+ b1 p + b0
y(t) = x(t) . (3-49)
an p n + an-1 p n-1+…+ a1 p + a0,
Это выражение формально совпадает с подобным выражением, определенным из (3-48). Следовательно, передаточная функция определяет связь между выходной и входной переменными в пространстве оригиналов.
Операторный полином левой части уравнений (3-46) и (3-47) характеризует собственные свойства системы, которые не зависят от внешних воздействий. Влияние воздействия описывается правым полиномом.
Характеристическое уравнение, соответствующее дифференциальному уравнению (3-57) имеет вид
аnln+an-1ln-1+…+a1l+ a0 = 0. (3-50)
Поэтому полином
D(p)= аnpn+an-1p-1+…+a1p+a0
называется характеристическим полиномом.
Динамическая система подвергается различным воздействиям. Обычно рассматривают некоторые, типовые. Зная реакцию на них, можно прогнозировать поведение системы в различных ситуациях.
Типовыми входными воздействиями принимаются:
1- единичная ступенчатая функция (единичный скачок)
f(t)= 1(t) {0 при t< 0; 1 при t>0};
2- единичная импульсная функция
f(t)= d(t);
3- гармонический сигнал
f(t)= b0 sin (wt).
Если собственные свойства описываются полиномом D(p), то с учетом типовых воздействий уравнение движения записывается в форме
x(t) ( аnpn+an-1pn-1+…+a1p+a0 )= f(t). (3-51)
Пусть f(t)= b1(t),тогда с учетом таблицы 3.1 в изображениях по Лапласу уравнение (3-51) можно переписать следующим образом
x(s)( аnsn+an-1sn-1+…+a1s+a0 )= b/s. (3-52)
Реакцию системы на скачок обычно называют переходной функцией. Для ее нахождения, как и в других случаях, могут применять табулированные функции, приведенные в таблице 3.1
В ряде ситуаций для определения переходных характеристик используют теорему о вычетах
x(t)=  Res {b/[D(s)s]}exp(st)½s=si. . (3-53)
Res {b/[D(s)s]}exp(st)½s=si. . (3-53)
Пример 3.1.
Найти переходную характеристику звена, имеющего передаточную функцию
W(s)= x(s)/y(s)= b/(1+Ts)
при скачкообразном внешнем воздействии y(t)= c*1(t).
Изображение внешнего воздействия будет иметь вид y(s)=c/s.
Уравнение движения в изображениях по Лапласу x(s)(1+Ts)= bc/s.
Здесь s1= -1/T; D’(s1)= T.
По формуле (2-47)
x(t)= bc/1 + bc/(-T-1T)exp(-t/T)= bc[1- exp(-t/T)]. (3-54)
Звено с такой характеристикой называется апериодическим 1-го порядка.
Пример 3.2.
Найти переходную характеристику звена с передаточной функцией
W(s)= x(s)/y(s)= b0/(1+a1s + a2s2)= b0/(1+ 2zTs+ T2s2)
при скачкообразном внешнем воздействии y(t)= c*1(t).
Уравнение движения в изображениях
x(s)( 1+ 2zTs+ T2s2)= b0c/s.
Таблица оригиналов функций Таблица 3.1.
| №№ | Оригинал | Изображение по Лапласу |
| 1(t) | 1/s | |
| tn | n!/sn+1 | |
| e-at | 1/(s+a) | |
| (1/a)(1-e-at) | 1/[s(s+a)] | |
| (e-at- e-bt)/(b- a) | 1/[(s+a)(s+b)] | |
| [(d-a)e-at- (d- b)e-bt]/ (b- a) | (s+ d)/[(s+ a)(s+ b)] | |
| (ab)-1+(be-at- ae-bt)/[ab(a- b)] | 1/[s(s+a)(s+b)] | |
| d/(ab)+ (d-a)e-at/[a(a -b)]+ (d- b)e-bt/[b(b- a)] | (s+d)/[s(s+a)(s+b)] | |
| l-1sin(lt) | (s2+ l2)-1 | |
| (d2+ l2)1/2l-1sin(lt+ y); y= arctg(l/d) | (s+ d)/(s2+ l2) | |
| l-1e-gtsin(lt) | 1/[(s+g)2+ l2] | |
| l-1[(d- g)2+ l2]1/2e-gtsin(lt+y); y= arctg[l/(d- g)] | (s+d)/ [(s+g)2+ l2] | |
| (g2+ l2)-1+ [l(g2+ l2)1/2]-1e-gtsin(lt- y); y= arctg[l(-g)-1] | 1/{s [(s+g)2+ l2]} | |
| d(g2+ l2)-1+ [l(g2+ l2)1/2]-1[(d- g)2+ l2]1/2 e-gtsin(lt+ y); y= arctg[l/(d- g) -]- arctg(l/g) | (s+d)/{s [(s+g)2+ +l2]} |
Пусть корни характеристического уравнения комплексные, т.е.
D(s)=a2{a-12+ sa1a-12 + s2)=a2(s+s1)(s+s2).
Тогда
s1,2={ - a1a-12 ± [(a1a-12)2- 4a-12]0,5}/2= { - a1a-12 ± j[4a-12 -(a1a-12)2]0,5}/2=
=-zT-1± [(z2-1)/T2]0,5= -z T-1± j[(1- z 2)/T 2]0,5= -a ± jw ,
где z <1.
Применив формулу (3-53), после раскрытия скобок и приведения подобных членов, получим
x(t)= bc{1- exp(-a t)[cos(wt)+ aw-1sin(wt)]}. (3-55)
T- называется постоянной времени звена; z - коэффициентом демпфирования.
Чем меньше Т , тем быстрее завершается переходный процесс. Значение z оказывает влияние на величину перерегулирования. Звено с такой характеристикой называется колебательным. Если z> 1, то корни характеристического полинома D(s) будут отрицательными действительными числами. Тогда переходная функция станет
x(t)= bc[1+ C1exp(l1t)+ C2exp(l2t)], (3-56)
где C1= l2/(l1- l2); C2= l1/(l2- l1); l1,2= -zT-1±T-1(z2-1)<0; C1<0; C2>0;
½l2 ½> ½l1 ½ .
Звено с такой характеристикой называется апериодическим 2-го порядка.
При z=1
x(t)= bc [ 1- (1+t/T)exp(-t/T)].
В случае z=0
x(t)= bc [ 1- cos(t/T))].
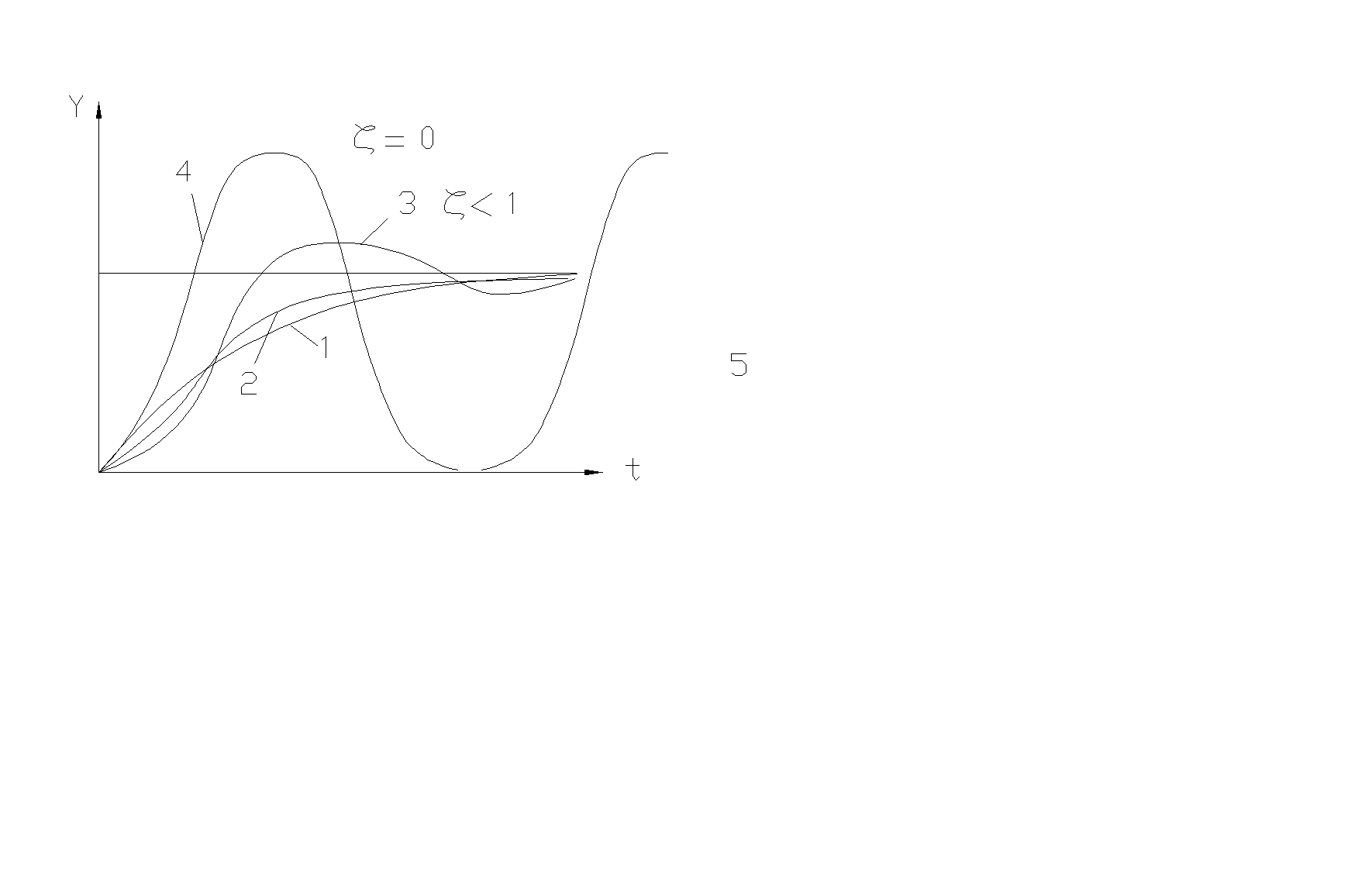
Звено с такой характеристикой называется консервативным. На рис. 3.7 показаны переходные характеристики рассмотренных звеньев.
 d(t)dt= 1 при любом e>0.
d(t)dt= 1 при любом e>0.
Реакция системы на единичную функцию называется весовой функцией. Она определяется дифференцированием переходной функции (см. рис. 3.8)
|
Рис. 3.7
Переходные характеристики:
1- апериодическое звено 1-го порядка;
2-апериодическое звено 2-го порядка;
3- колебательное звено; 4- консервативное звено (z=0).
Единичной импульсной функцией (единичной d- функцией) называют функцию, равную нулю всюду, кроме t= 0, где она стремится к бесконечности, причем так, что k(t)= dx(t)/dt.
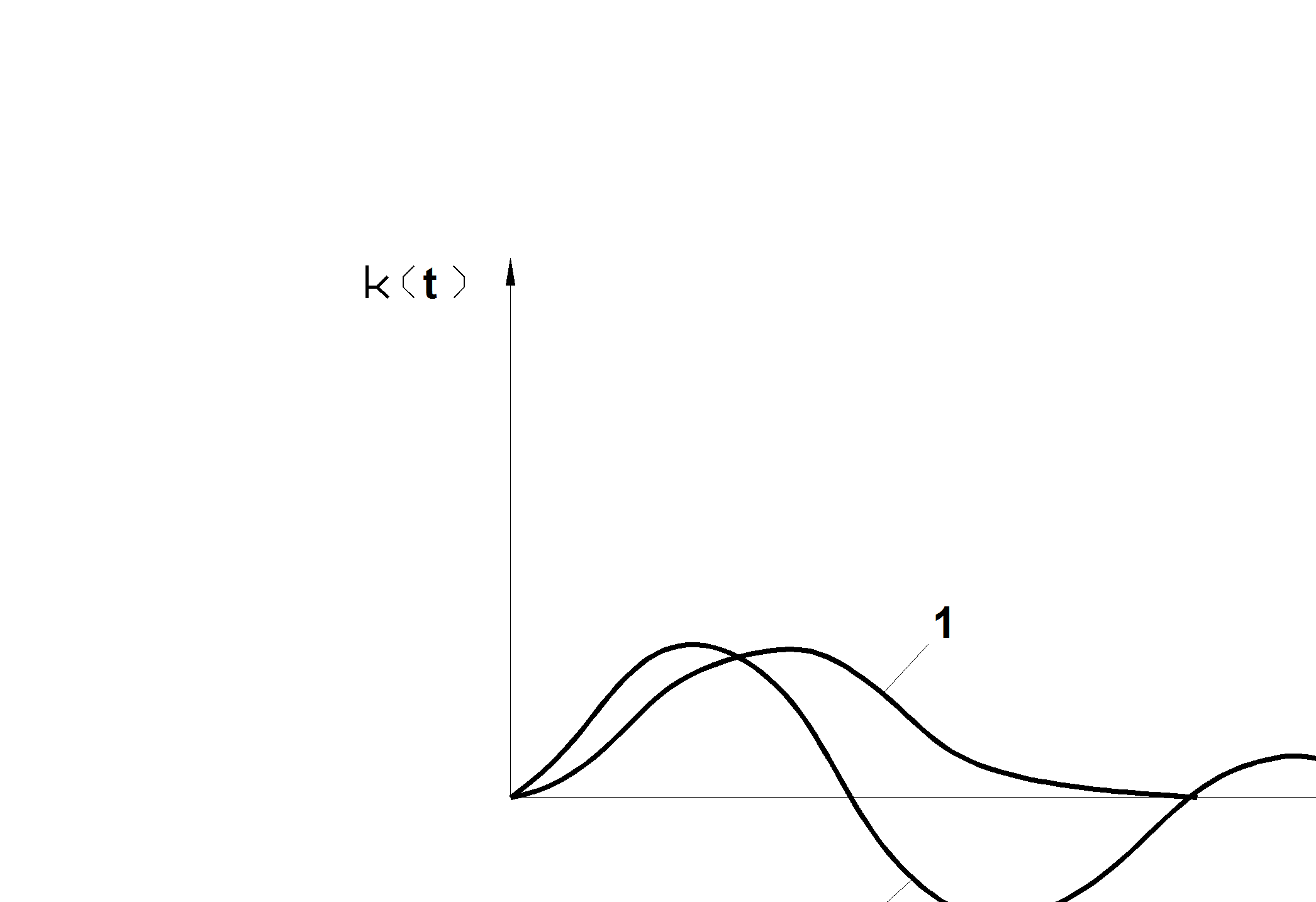
Рис.3.8
Весовые функции:
1- апериодическое звено 2-го порядка;
2- колебательное звено.
Иногда последнее выражение записывают в форме
k(t)= dh(t)/dt,
где h(t) - обозначена переходная функция x(t).
Передаточная функция является изображением по Лапласу весовой функции.
Если на вход системы , звена подается гармонический сигнал
x(t)= aвхsin (wt),
то в силу линейности исходного дифференциального уравнения выходная координата будет изменяться по гармоническому закону (см. рис. 3.9)
y(t)= bвых sin(wt+ j). (3-57)
Здесь w - угловая (круговая) частота; bвых - амплитуда гармонических колебаний выходной величины; j - сдвиг по фазе выходной величины относительно входной (j=wtc).
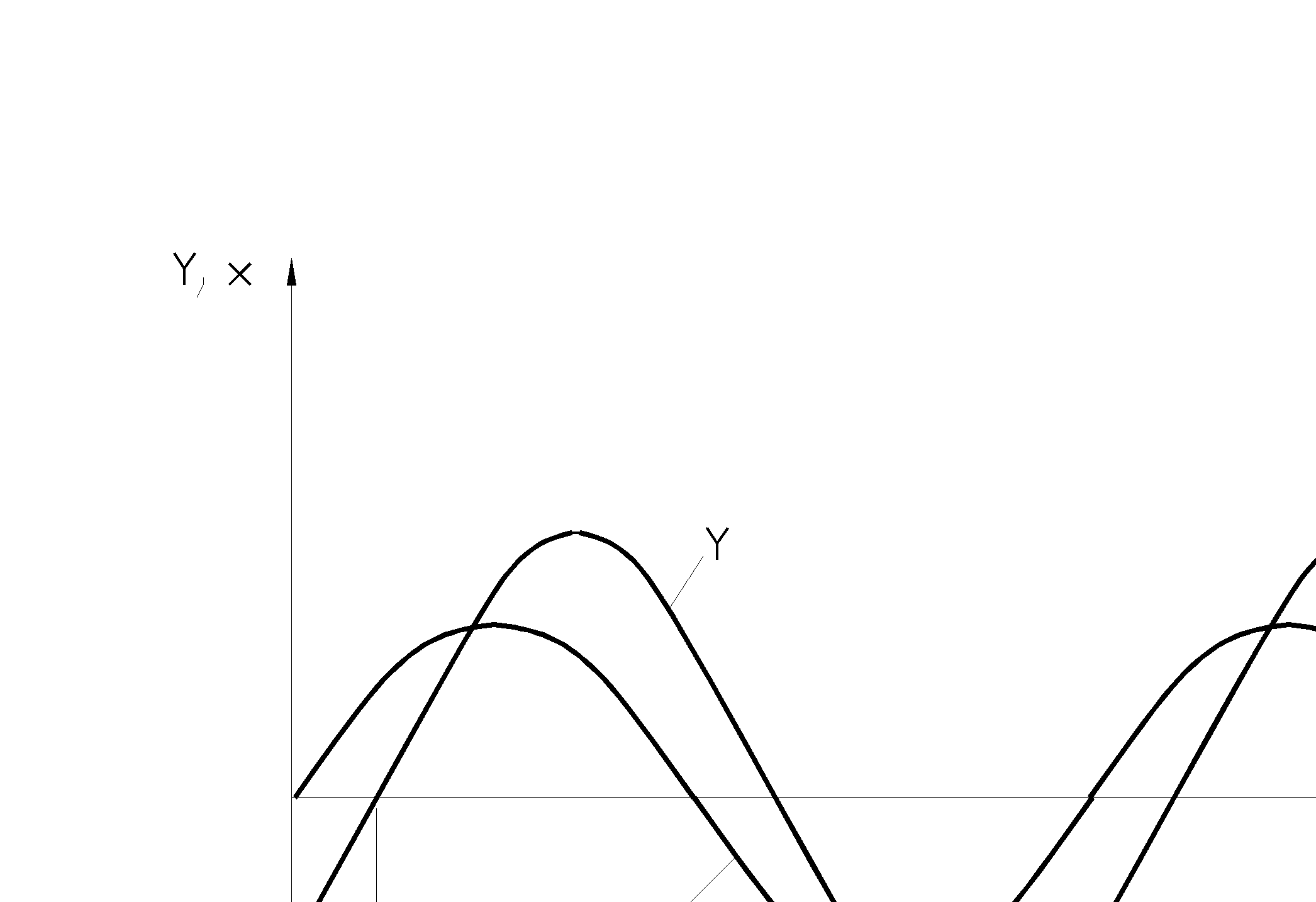
Рис. 3.9
Соотношение колебаний на входе и выходе звена или системы.
Для определения решения в комплексной области положим
X= aвхexp(jwt), Y= bвыхexp[j(wt+ j)]. (3-58)
Подставим выражения (3-69) в дифференциальное уравнение (3-57)
[an(jw)n+ an-1(jw)n-1+… +a1(jw)+ a0]bвыхexp(jj)exp(jwt)=[bm(jw)m+ bm-1(jw)m-1+…
…+ b1(jw)+ b0]aвхexp(jwt). Сократив обе части уравнения на необращающийся в нуль множитель exp(jwt), найдем комплексную величину
W(jw)=(bвых/aвх)exp(jj)=[bm(jw)m+ bm-1(jw)m-1+…+ b0]/
/[an(jw)n+ an-1(jw)n-1+… +a1(jw)+ a0]. (3-59)
Выражение (3-59) называется амплитудно- фазовой частотной характеристикой (АФЧХ).
АФЧХ можно определить из передаточной функции, подставив s=jw .
Комплексная величина (3-59) на комплексной плоскости (jV, U) является годографом радиуса- вектора W(jw) при изменении частоты w от нуля до бесконечности. Длина радиуса - вектора A(w)= bвых/aвх равна отношению амплитуд выходной и входной величин, а угол между радиусом- вектором и положительной частью вещественной оси равен сдвигу по фазе между колебаниями этих величин, т.е.
½W(jw)½= A(w), argW(jw)= j(w). (3-60)
С учетом этого
W(jw)=A(w)exp(jj) (3-61)
или
W(jw)= U(w)+ jV(w), (3-62) где U(w) и V(w) соответственно, вещественная и мнимая части характеристики.
При проведении экспериментов часто динамические свойства систем определяют по экспериментальным частотным характеристикам, подавая с помощью различных устройств на вход гармонический сигнал и фиксируя, например, с помощью осциллографа, колебания выходной координаты.
В зависимости от вида передаточной функции АФЧХ имеет разную форму. На рис. 3.10 показаны частотные характеристики апериодического звена 1-го порядка (1) и колебательного звена (2).
При расчетах и исследованиях динамических свойств часто используют логарифмические амплитудно- частотные (ЛАЧХ) и фазо- частотные (ЛФЧХ) характеристики, которые иногда называют диаграммами Боде. ЛАЧХ и ЛФЧХ определяют следующим образом
L= 20lg½A(w)½, дБ, j= arctg[V(w)/U(w)], рад. (3-63)
Каждое звено и система имеют собственную ЛАЧХ и ЛФХ.
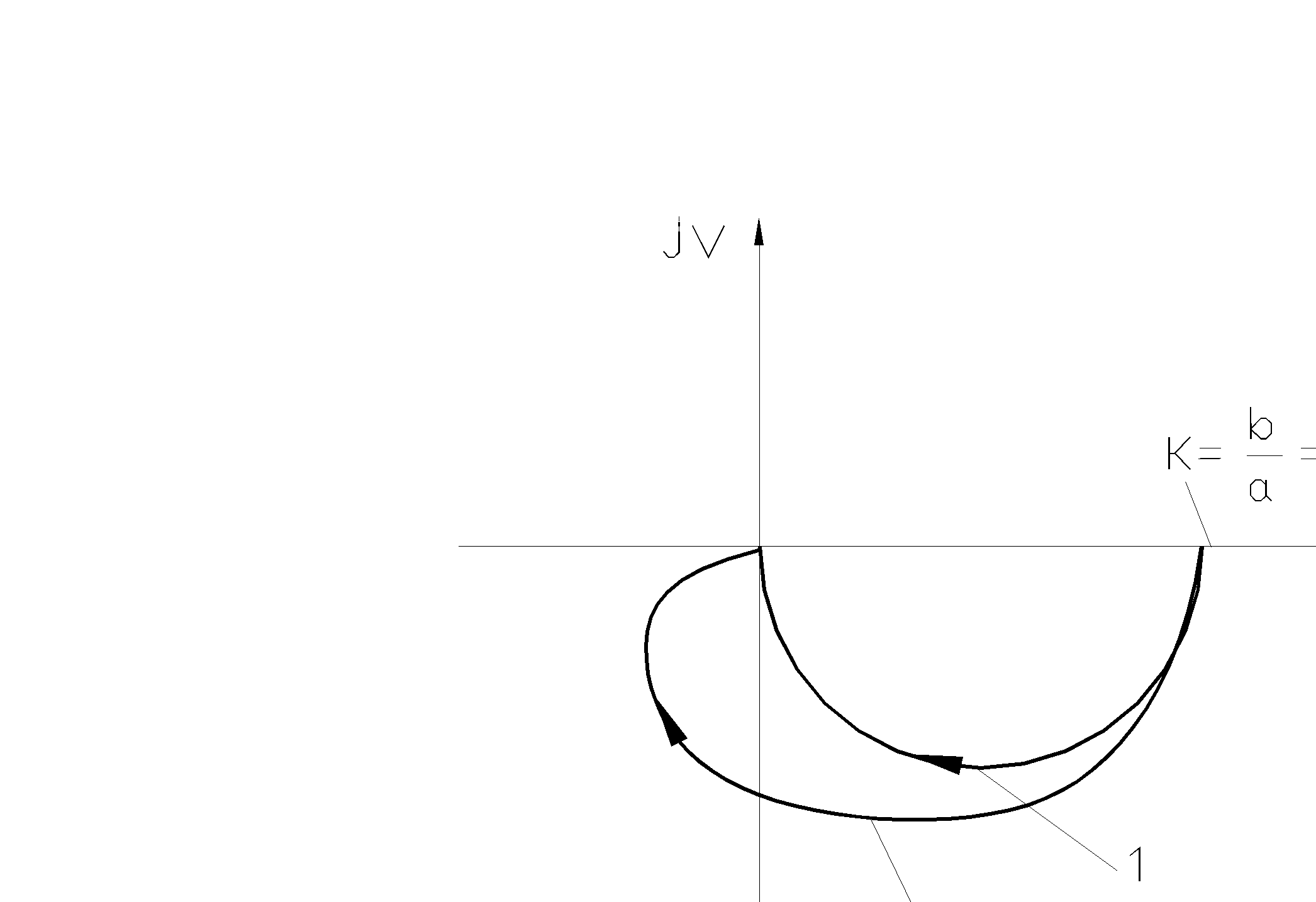
Рис. 3.10
Частотные характеристики.
Критерии устойчивости
Критерий Михайлова.
Для устойчивости линейной системы требуется, чтобы все корни характеристического многочлена
D(l)= a0ln+ a1ln-1+… + an-1l+ an
или
D(s)= a0sn+ a1sn-1+… + an-1s+ an (3-64)
были отрицательными, если они вещественны, или имели отрицательные вещественные части, если они комплексные.
При высоких порядках уравнения D(l),D(s) поиск корней аналитическими методами затруднителен или невозможен. Для решения такой задачи введем в D(s) s=jw. Критерий Михайлова формулируется следующим образом.
Динамическая система устойчива, если при возрастании w от нуля до бесконечности вектор D(jw)повернется на угол pn/2, где n - степень характеристического многочлена D(l) или, что тоже самое, если характеристическая кривая D(jw) при изменении w от нуля до бесконечности обходит, начиная с положительной действительной полуоси, последовательно в положительном направлении (против движения часовой стрелки) n- квадрантов.
Кривая, которую описывает своим концом вектор D(jw) называется частотным годографом Михайлова.
Дата добавления: 2015-02-23; просмотров: 1008;
