В механизме.

В процессе работы детали механизма (магистрали) передают мощность N=Fu, определяемую выходными координатами, скоростью движения и силой сопротивления. В самом механизме мощность тратится на перемещение отдельных частей и на их деформацию. В первом случае часть подведенной энергия является кинетической, во втором- потенциальной. Кинетическая составляющая потерь мощности определяется кинематикой механизма. Потенциальная составляющая приводит к переменным напряжениям в магистралях, нагреву и т.п.

Рассмотрим продольные колебания.

Величина удельной накопленной потенциальной энергии w_п для продольной упругой деформации при отсутствии поперечных сил определим следующим образом (см. 2-54).

w_п=0,5es = 0,5s ²/Е.

Следовательно, удельная мощность, выделяемая в единице объема стержня при продольной деформации, будет

N_у= d w_п/dt= (s/Е)ds/dt.

Таким образом, зная закон изменения напряжения можно определить и изменения мощности в сечении стержня.

Для крутильных колебаний удельная потенциальная равна (см. (2-100))

w_п =0,5t ²_мах k_fJ /G,

где k_fJ = J_p/(fy²_max).

Для круга будет

w_п =0,25t²_махG^-1.

Таким образом, удельную мощность, выделяемую в элементарном объеме стержня при кручении можно представить выражением

N_yк= dw_п /dt=( k_fJ t_мах /G)dt_мах /dt. (3-26)

Для круга получим

N_yк= (0,5 t_мах /G)dt_мах /dt.

Рассмотрим далее колебания в стержне, заделанным одним концом и нагруженным изгибающим моментом, действующим в плоскости изгиба.

Если полагать, что статический момент сечения относительно нейтральной оси равен нулю, то изгибающий момент, передаваемый стержнем

М_и = E J_z /r=s_u W_z,

где J_z , W_z= J_zy^-1_max- моменты инерции и сопротивления сечения; y_max - максимальная координата относительно нейтральной оси сечения; r - кривизна.

Угол поворота двух смежных сечений, расположенных на расстоянии dx друг от друга, равен dj= dx/r.

Поскольку r= EJ_z/M_u , то dj=( M_u/EJ_z) dx.

Потенциальная энергия деформации, накопленная участком стержня длиной dx, равна работе моментов М_u, приложенных по торцам этого участка

dA_p= 0,5М_udj.

Подставим в это выражение М_и =s_u W_z и разделим обе части на dV= fdx,

w_п= 0 ,5k_sJ s²_uE^-1 ,

где k_sJ = J_z/(fy²_мах).

Для круга будет w_п= 0 ,125s²_uE^-1.

Величина w_п представляет собой потенциальную энергию, накопленную в каждом элементарном объеме изгибаемого стержня.

Таким образом, мгновенное значение удельной мощности, выделяемой в элементарном объеме стержня при изгибе, можно описать выражением

N_yи= dw_п /dt= ( k_ss_u /E)ds_u /dt. (3-27)

В связи с тем, что в процессе работы деталь претерпевает различные формы деформации, то, следуя энергетической теории прочности, введем в рассмотрение интенсивность деформаций [3]

e _i= [2^1/2(1+ c)]^-1[(e _y- e _z)²+(e _z -e _x)²+(e _x- e _y)²+

+ 1,5(g_yz²+ g_zx²+ g_xy²)]^1/2

и интенсивность напряжений

s_i= 2^-1/2[(s_z -s_y)²+ (s_y- s_x)²+ (s_z- s_x)²+ 6(t_xy²+ t_zx²+ t_yz²)]^1/2,

где s_z, e _z; s_x, e _x; s_y, e _y – соответственно, нормальные напряжения и относительные деформации в направлении осей координат Z, X, Y; t_xy, g_xy; t_zx, g_zx; t_yz, g_yz – соответственно, касательные напряжения и углы поворота граней.

Пусть при интенсивности деформации на dl/l= e_i участка длиной l и элементарной площадью сечения интенсивность напряжений составляет s_i. Тогда, учитывая обобщенный закон Гука s _i = e _i Е_i, где Е_i= Е’ - обобщенный модуль упругости (см. также (2-78)), элементарная накопленноя энергия

w_i=0,5e _i s _i = 0,5s ²_i / Е_i .

Следовательно, удельная мощность, выделяемая в единице объема стержня при некоторой деформации, будет

N_уi= d w_i /dt= (s _i / Е_i )ds _i /dt. (3-28)

Полученные соотношения позволяют через колебания напряжений в магистралях описать изменения потенциальной составляющей удельной мощности в механизмах.

Если напряжения в деталях механизма превышают некоторые допустимые значения, то механизм может перестать работать. В связи с тем, что в большинстве случаев различные устройства работают при переменных нагрузках, то их ресурс часто зависит от колебаний напряжений в магистралях, деталях.

Выше показано, что при любой деформации совершается некоторая работа. Следовательно, в случае колебаний в элементарном объеме может накапливаться определенное количество энергии. Однако из-за теплопередачи она отводится. Если количество подведенной энергии равно количеству отведенной Q_отв, то нагревания не будет и металл, по всей видимости, может воспринимать практически любое количество циклов деформации. Поэтому для оценки динамической прочности металлических деталей необходимо знать разницу D А_р= А – -Q_отв .

Подводимая в сечение мощность распределяется следующим образом

N_e= 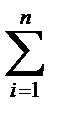D T_i/R_i ,

где D T_i , R_i - перепад температур и термосопротивление в направлении теплопередачи; n - номер канала передачи тепла.

Если магистраль, по которой передается соответствующая мощность, является однородной, т.е. по всей длине размеры, плотность и др. одинаковы, то мощность, затрачиваемая на продольные колебания стержня, равна

N_e= V (s/Е)ds/dt, (3-29)

где V - объем деформируемого участка.

Часть подведенной мощности сразу отдается в окружающую среду, а часть отводится через контакты с другими металлическими деталями. Оставшаяся мощность идет на нагревание стержня. Например, при испытаниях на усталость по ГОСТ 25.502-79 подводимая энергия отводится в окружающую среду- воздух или смазочно-охлаждающую среду (СОС), через контакт в детали машины для испытаний. Кроме того, образцы выполняются строго определенных размеров, а частота колебаний в процессе испытаний поддерживается постоянной. В указанном нормативном документе отмечено, что при саморазогреве выше некоторых температур уровень частот ограничивается.

Если подводимая мощность равна отводимой посредством теплопередачи, то температура зоны деформации будет постоянной. В этом случае материал может эксплуатироваться весьма долго. В противном случае- оставшаяся энергия будет накапливаться в кристаллической решетке и через определенное количество циклов вызовет разрушение.

Допустим, что интенсивность напряжения в магистрали какого- либо механизма изменяется по гармоническому закону s_i = s_аsin(wt) (см. рис.3.6).

В этом случае при продольных колебаниях стержень получает мгновенную мощность

N_пмгн= Vs_а²w Е_i ^-1 sin(wt)cos(wt)= 0,5Vs_а²w Е_i ^-1 sin(2wt) , (3-30)

За время, равное одному циклу колебаний напряжения t= 2p/w, полученная энергия составит

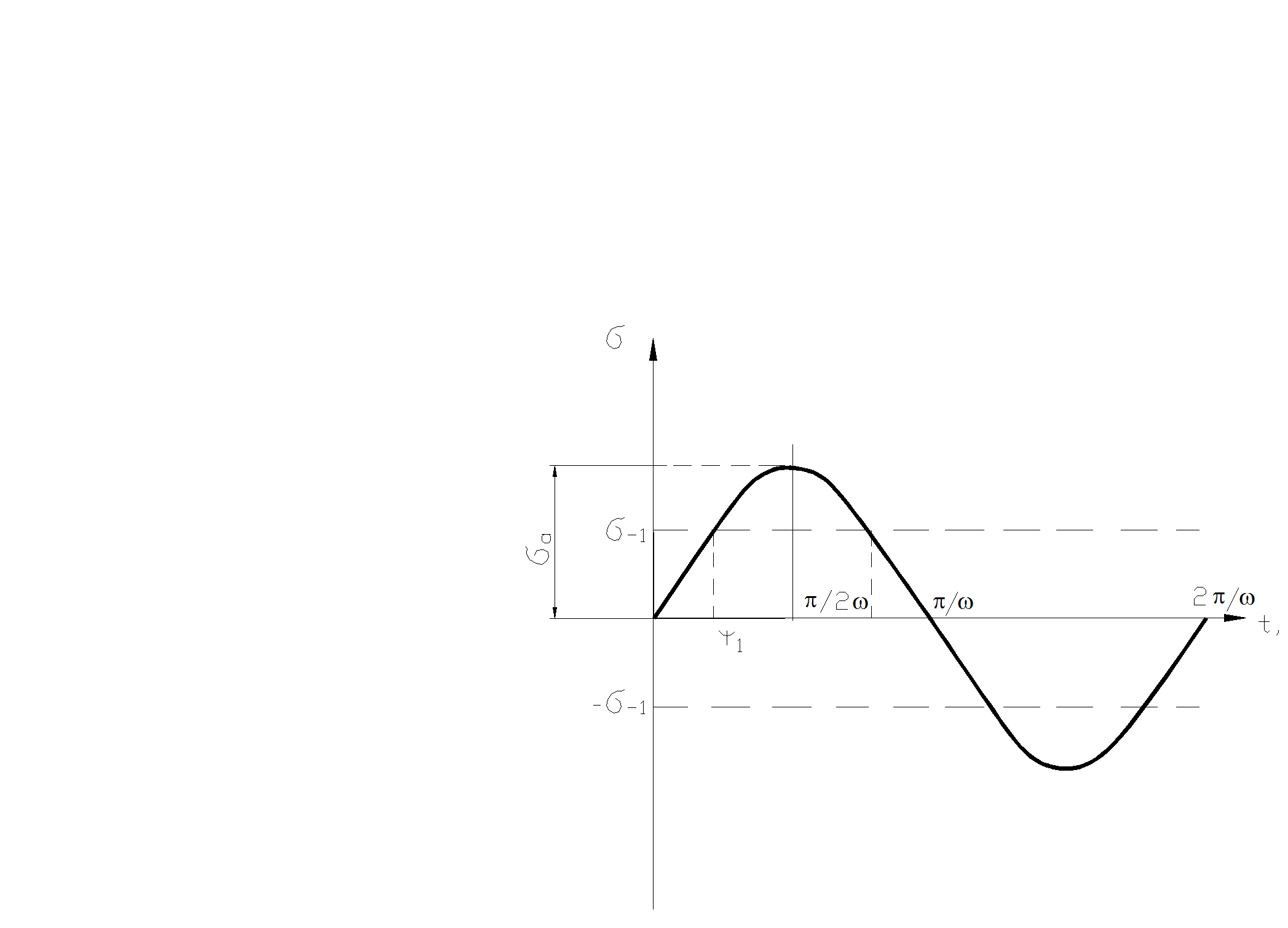
Рис. 3.6

Колебания напряжений в магистрали механизма (s_-1- предел выносли-вости при симметрич-ном цикле нагружения, определяемый на образце).

А_цп = 4 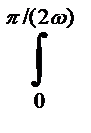N_пмгн dt= 4*0,5Vs²_a w Е_i^-1 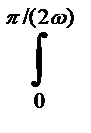sin(2wt)dt=

= - Vs²_a Е_i^-1cos(2wt)| 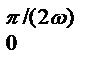= 2Vs²_a Е_i^-1. (3-31)

Из приведенного следует, что удельная мощность, выделяемая в объеме стержня, изменяется по закону синуса двойного угла y_N= 2wt с частотой w_N= 2w. Время ее периода равно t_п= p /w. За время эксплуатации t_э механизма число таких периодов составит z= w t_э/p. Тогда общее количество энергии, затрачиваемой на деформацию кристаллических решеток объема, будет

А_п = z А_цп= 0,637Vw t_эs ²_a(1/ Е_i). (3-32)

Заметим, что в элементарном объеме за период t_э будет выделяться энергия

А_qп= 0,637w t_эs ²_a(1/ Е_i). (3-33)

Положим, как и Одинг И.А., что разрушение участка детали наступает тогда, когда количество тепла, оставшегося в каком-либо участке, соответствует удельной энергии, достаточной для плавления, т.е.

A_q@ rcT_s [ Дж/м³], (3-34)

где c- удельная теплоемкость [Дж/(кг*град)]; T_s - абсолютная температура плавления металла [град]; r - плотность материала [кг/м³].

Тогда время эксплуатациидетали будет

t_э= r c Е_i T_s/(0,637xws ²_a). (3-35)

а число циклов деформации-

Z=0,5r c Е_i T_s/(xs ²_a), (3-36)

где x - коэффициент, учитывающий долю подведенной мощности, затраченной на нагревание элементарного объема детали.

К сожалению, использовать изложенный прием можно лишь при знании значений коэффициента x и термосопротивлений, сведений о которых в настоящее время недостаточно. Однако в предположении, что эти параметры в случае сравнения результатов испытаний в подобных условиях для подобных деталей одинаковы, он позволяет оценить влияние остальных факторов (объем и форму детали, амплитуду колебаний напряжений и т.п.), на допускаемое количество циклов нагружений другой детали.

Таким образом, зная амплитуду колебаний и частоту изменения напряжения в работающей конструкции, можно с помощью выражений (3-35), (3-36) оценить ресурс той или иной детали изделия. Ход процесса разрушения определяется многими факторами и изучается специальными научными направлениями.

В связи со сложностью решения задач по определению термосопротивлений каналов передачи тепла при оценке надежности той или иной конструкции применяют разнообразные критерии. Обычно такой расчет выполняют с помощью соотвествующих графиков и таблиц, где учитываются размеры, наличие концентраторов напряжений, смазка и др. Примеры расчетов на прочность с учетом описанных факторов приведены в разделах 5.16, 5.23, приложениях.

При колебаниях выражение N(t)= u(t)F(t), где u - скорость движения выходной координаты механизма,не совсем правильно отражает колебания мощности в механизме. Действительно, пусть сила сопротивления изменилась скачкообразно F(t)= F₀ *1(t). Тогда, если пользоваться указанной формулой, о колебаниях мощности можно судить фактически по изменению скорости движения выходной координаты. Однако, известно, что скорость движения выходной координаты, например частота вращения соединительной муфты редуктора, обычно равна скорости движения прилегающего к ней участка силовой магистрали (выходного вала редуктора). При этом в динамическом процессе в сечении вала происходит изменение напряжений. В зоне, прилегающей к указанной муфте, это максимальные касательные напряжения. Тогда колебания мощности в выходном участке силовой магистрали (вала) можно описать выражением

N(t)= t _max(t) W_p W (t) , (3-37)

где W, W_p - угловая скорость вращения выходного участка магистрали, равная скорости вращения соединительной муфты, и геометрический полярный момент сопротивления сечения этого участка.

Если же взять выходные параметры редуктора, то будет

N(t)= M_c0 W (t).

Очевидно, соотношение (3-37) более точно отражает динамику энергетических затрат устройства.

Кинетическая составляющая потерь мощности в механизмах зависит от масс деталей и их скоростей движения.

В большинстве случаев эта составляющая при равномерном движении тратится на перемешивание рабочей среды, например масла, трение. Ее можно учитывать в коэффициенте потерь, пропорциональных скорости движения. Однако, следует иметь в виду, что во время изучения колебаний обычно коэффициент отмеченных потерь включает также и потери, пропорциональные скорости движения в нагрузке. Инерция движущихся масс механизма при этом учитывается в приведенных моменте инерции или массе.