Билет 11

2. Тиск під викривленою поверхнею (формула Лапласа)

Розглянемо тонку плівку, товщиною якою можна знехтувати. Прагнучи мінімізувати свою вільну енергію, плівка створює різницю тиску з різних сторін. Цим пояснюється існування мильних бульбашок : плівка стискається до тих пір, поки тиск всередині міхура не буде перевищувати атмосферний на величину додаткового тиску плівки. Додатковий тиск в точці поверхні залежить від середньої кривизни в цій точці і дається формулою Лапласа:

,

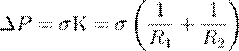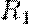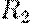де і — радіуси головних кривизн в точці. Вони мають однаковий знак, якщо відповідні центри кривизни лежать по одну сторону від дотичної площини в точці, і різний знак - якщо по різні боки.

Наприклад, для сфери, центри кривизни в будь-якій точці поверхні збігаються з центром сфери, тому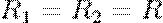

Для випадку поверхні кругового циліндра радіуса R маємо ,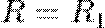

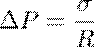
Зверніть увагу, що Δ p має бути безперервною функцією на поверхні плівки, так що вибір "позитивної" сторони плівки в одній точці локально однозначно задає позитивний бік поверхні в досить близьких її точках.

З формули Лапласа випливає, що вільна мильна плівка, натягнута на рамку довільної форми і не утворює міхурів, буде мати середню кривизну, що дорівнює 0.

П.н. твердих та рідких тіл залежить від температури (рис. 2). З підвищенням температури П.н. зменшується, оскільки послаб­люється когезія. Як показав Д.І. Менделєєв, при достатньо низькій критичній температурі Т_кр П.н. дорівнюватиме нулю. Залежність П.н. від абсолютної температури має вигляд:

σ_Т = β (Т_кр — Δ — Т) σ₀,

де β — коефіцієнт пропорційності; Δ — поправка (6°); Т_кр та Т — критична температура та температура досліду відповідно; σ₀— П.н. при початковій температурі; σ_Т— П.н. при температурі досліду.