Билет 16

1.Поскольку газ идеальный, 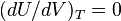и внутренняя энергия остается постоянной. Все тепло, полученное от резервуара при температуре 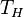, превращается во внешнюю работу:

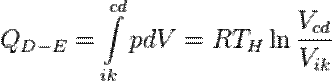. [1]

Процесс В-C. Подобным же образом, работа, совершенная при сжатии, превращается в тепло, которое передается холодному резервуару:

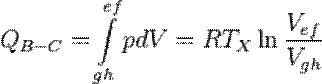. [2]

Процессы E-B и C-D. Поскольку газ идеальный и 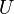зависит только от температуры 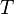, из уравнения 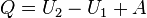следует, что работа, совершаемая в одном из этих двух адиабатических процессов, полностью компенсирует работу, совершаемую в другом процессе. Действительно, пользуясь адиабатическим условием 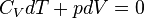, получаем:

.

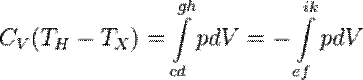Чтобы найти связь между 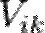, , 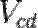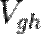и 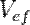, заметим, что, согласно уравнению Пуассона 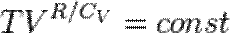, в адиабатических процессах:

(E → B):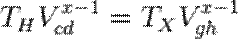

(C → D):

и, следовательно, .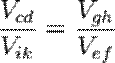

Подставляя это соотношение в уравнения [1] и [2], получаем:

.

В то же время мы приходим к результату… что КПД оптимального цикла равен .»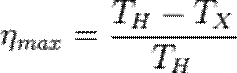

2. Теплопровідність– передача енергії від більш нагрітих частин тіла до менш нагрітих, що приводить до вирівнювання температур. У процесі теплопровідності енергія атомів і молекул більш нагрітих ділянок речовини передається сусіднім, холоднішим. З часом, унаслідок зіткнення молекул, відбувається вирівнювання їх середніх кінетичних енергій, а значить і температури (приклад – нагрівання ложки у стакані з гарячим чаєм). Формула теплопровідності виглядає наступним чином: Q =? * (DT/dx) * S * d ?, де: Q - теплопровідність ;? - Коефіцієнт теплопровідності; (dT/dx) - градієнт температури; S - площа поперечного перерізу

Густина потоку тепла є кількість теплоти 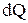, що переноситься через одиничну площадку 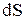за одиницю часу 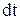: q_n= .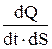

Оскільки однакова кількість теплоти, що підводиться через прошарок за одиницю часу з одного боку на поверхню стінки В, проходить крізь усі шари стінки і виводиться через поверхню А в навколишнє середовище, то для кожного шару стінки площею S можна записати

;

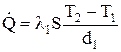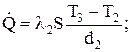
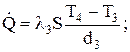
Розділивши (2.2) і (2.4) на (2.3), отримаємо

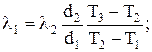l₃ =l₂ 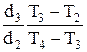. (2.5)

Знаючи коефіцієнт теплопровідності середнього шару, можна визначити його значення для інших шарів, вимірявши товщину шарів і визначивши різниці температур. При однаковій товщині зразків формули (2.5) спрощуються і можуть бути використані для відносного визначення коефіцієнта теплопровідності.