Шарнирно-сочлененные стреловые системы

Принцип действия шарнирно-сочлененных стреловых систем с прямым хоботом основан на свойстве некоторых шарнирных механизмов воспроизводить траектории, на некотором участке мало уклоняющиеся от прямой. Методика синтеза таких механизмов подробно разработана П.Л. Чебышевым. На рис. 1.39 показан так называемый симметричный прямолинейно направляющий механизм Чебышева, у которого звенья TU = O₁U = UV. Точка Т шатуна TUVпри полном обороте кривошипа О₃V описывает траекторию, которая на выделенном участке близка к прямой линии.

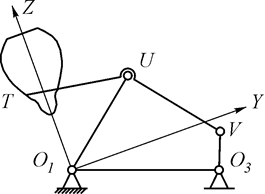
Рис. 1.39. Механизм П.Л. Чебышева

Шарнирно-сочлененное стреловое устройство с постоянной длиной подвеса груза (рис.1.40,а,б) представляет собой четырехзвенный механизм, состоящий из стрелы 1, хобота 2, шарнирно присоединенного к стреле и оттяжке 3, и неподвижной стойки, на которой закреплены нижние шарниры стрелы и оттяжки. Стойка оформляется в виде рамного или решетчатого каркаса или балочной колонны.

Чтобы траектория груза была эквидистантна траектории конца хобота и столь же мало уклонялась от горизонтали, грузовой канат надо направить вдоль стрелы (рис. 1.40,а) или оттяжки (рис. 1.40,б).

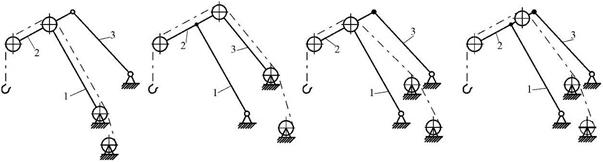
Рис. 1.40. Схемы шарнирно-сочлененных стреловых систем с прямым хоботом

В первом случае усилие в канате нагружает стрелу дополнительным сжатием; во втором случае усилие в канате уменьшает усилие в растянутой оттяжке. Поэтому направление каната вдоль оттяжки предпочтительнее. Обе схемы накладывают на компоновку поворотной части жесткие ограничения, поскольку расположение блоков должно быть согласовано с расположением шарниров стрелового устройства.

В схеме на рис. 1.40,а для прилегания канатов к блокам в корне стрелы нужно выдвигать лебедку вперед, что неудобно и для грейферных кранов часто требует соосного расположения замыкающего и поддерживающего барабанов. В схеме на рис. 1.40,в блоки на колонне не совпадают с нижними шарнирами стрелы и оттяжки, и траектории груза и конца хобота не эквидистантны. Движение груза по траектории, мало уклоняющейся от горизонтали, есть результат наклона стреловой системы и перекатывания каната по блокам. Недостаток схемы — дополнительный износ каната из-за перекатывания. Ее преимущества — более широкие возможности при компоновке, большее число параметров, на которые можно воздействовать при синтезе схемы, и меньшие, чем в схемах с направлением каната вдоль звеньев, длина хобота и величина крутящего момента, нагружающего стрелу при боковом отклонении грузовых канатов (что особенно важно для решетчатых стрел). Развитием этой схемы является схема на рис. 1.40,г, где блок на хоботе не совпадает с шарниром стрела-хобот.

Определение грузового неуравновешенного момента M_G рассмотрим на примере схемы шарнирно-сочлененного стрелового устройства с прямым хоботом и произвольным расположением отклоняющего блока на хоботе (рис. 1.41). (Метод определения M_G графическим способом представлен на рис. 1.64.) Введем дополнительно к прямым стрелам еще две КПФ первого порядка:

, ,

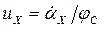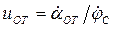положительные направления углов a_Х и a_ОТпоказаны на рис. 1.41.

Введем некоторые промежуточные соотношения. В соответствии со схемой на рис. 1.41 расстояние между точками О_Си О₃

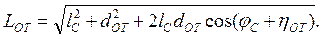(1.48)

Определим величины D₁ и D₂ зависимостями вида

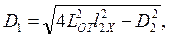
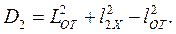(1.49)

В этих выражениях величины l_С,l_2Х,l_ОТ — соответственно длины стрелы, заднего плеча хобота и оттяжки.

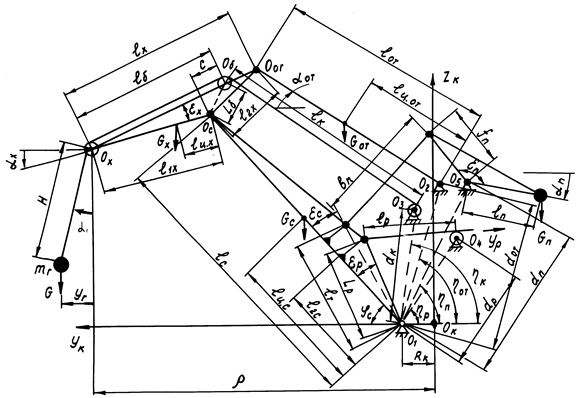
Рис. 1.41. Схема системы изменения вылета портального крана с верхним уравновешиванием на качающемся рычаге

Длина оттяжки l_ОТ определяется по выражению

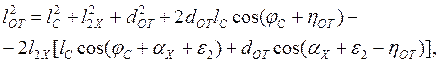(1.50)

где 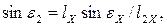(1.51)

а связь между углом наклона хобота a_Х, параметрами стреловой системы и углом наклона стрелы определяется выражением

tga_X = (D₁B₁ – D₂B₂) / (D₁B₂ +D₂B₁),(1.52)

где D₁и D₂ определяются по выражениям (1.49), а В₁ и В₂ – по выражениям:

B₁ = l_C cos(j_C + e₂) + d_ОТ cos(h_ОТ – e₂),B₂ = l_C sin(j_C +e₂) – d_ОТ sin(h_ОТ – e₂).

Дифференцируя по времени выражение (1.52), после соответствующих преобразований найдем u_Х по формуле

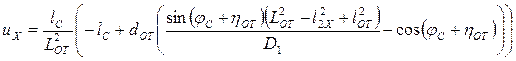(1.53)

Тригонометрическая функция угла a_ОТ в соответствии со схемой на рис. 1.37:

sina_ОТ = (l_С sinj_С +l_2X sin(a_X +e₂) – d_ОТ sinh_ОТ )/ l_ОТ,(1.54)

где l_ОТи sine₂ определяются соответственно по формулам (1.50) и (1.51).

После дифференцирования по времени соотношения (1.54) и соответствующих преобразований получим величину u_ОТ по формуле

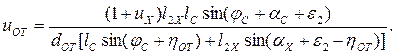(1.55)

Для шарнирно-сочлененных стрел связь между углом наклона стрелы j_С, параметрами стреловой системы и ее вылетом r задается зависимостью

r = R_K + l_C cosj_C + l_1X cosa_X. (1.56)

Тогда кинематическая передаточная функция первого порядка

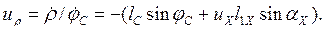(1.57)

Кинематическая передаточная функция первого порядка

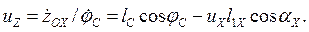(1.58)

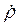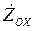Здесь и представляют собой соответственно горизонтальную и вертикальную проекции абсолютной скорости конца хобота (точки ОX) на соответствующие оси. С помощью u_r можно пересчитывать горизонтальную нагрузку, приложенную к концевым блокам хобота, на момент относительно корня, с помощью u_Z — вертикальную нагрузку.

Определим кинематическую передаточную функцию первого порядка u_К. Координата z_Г центра масс груза (см. рис. 1.41) определяется по формуле

Z_Г = l_С sinj_С – l_1X sina_X – (H_O + H_ПЕР), (1.59)

где приняты обозначения, как в формуле (1.31) и (1.32). При неработающем механизме подъема общая длина L_К грузового каната

L_К = (H_O + H_ПЕР) u_ПОЛ + l_К + l_Б, (1.60)

где l_К и l_Б – длины участков канатов на рис. 1.41, причем l_Б = const, а l_Копределяется из выражения

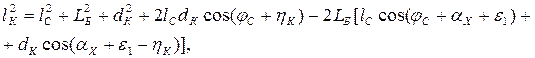(1.61)

где 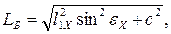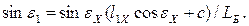(1.62)

Продифференцировав зависимость (1.60) по времени, найдем значение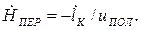

Теперь с использованием зависимости (1.61), можно получить КПФ u_Кпо формуле

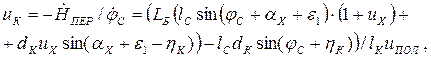(1.63)

где l_К определяется по (1.61).

Грузовой неуравновешенный момент М_G определяется по (1.40), u_G — по (1.39), u_Z — по (1.58), u_К — по (1.63).

Если отклоняющий блок на хоботе совмещен с концевыми блоками стрелы (L_Б = 0) и канат идет вдоль стрелы (d_К = 0), перекатывания канатов по блокам при изменении вылета крана не происходит (u_К = 0). Если канат идет вдоль оттяжки, то в (1.63) следует положить L_Б = l_2Х, d_К = d_ОТ, l_К = l_ОТ, h_К = h_ОТ и получим u_К = 0.

Полученные выражения для КПФ первого порядка после преобразований можно представить в виде, общем для прямых стрел с уравнительным полиспастом и шарнирно-сочлененых стрел:

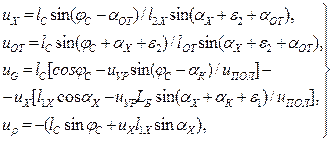(1.64)

где a_К – угол наклона канатов

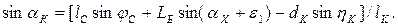(1.65)

Для прямых стрел с уравнительным полиспастом в формулах (1.64) следует положить u_Х и L_Бравными нулю, для шарнирно-сочлененных стрел — u_УР = 1. При общем поле параметров это позволяет проводить не только параметрическую, но и структурную оптимизацию стреловых устройств.

Процесс определения параметров стрелового устройства графическим методом при соблюдении многочисленных компоновочных ограничений и удовлетворительности траектории груза весьма длителен и трудоемок [5]. Задача синтеза стрелового устройства в полной мере решается с применением ЭВМ [15].

Шарнирно-сочлененные стреловые устройства с профилированным хоботом в современных конструкциях кранов не используются, так как профилированный хобот сложен в изготовлении и его конструкция отличается от коробчатой конструкции, повсеместно вытесняющей решетчатую.