Прямые стрелы с уравнительным полиспастом

Схема прямой стрелы с уравнительным полиспастом представлена на рис. 1.37. Грузовой канат идет от барабана механизма подъема и образует уравнительный полиспаст кратностью u_УР между блоками О₂ на колонне крана и О_С на конце стрелы, а далее направляется в грузовой полиспаст кратностью u_ПОЛ и крепится на стреле (при четных u_ПОЛ) или на подвеске (при нечетных u_ПОЛ) (рис. 1.59). При изменении вылета, когда механизм подъема не работает, длины грузового Н и уравнительного l_К полиспастов изменяются в противоположных направлениях, что позволяет обеспечить траекторию груза, близкую к горизонтальной прямой. Грузовой неуравновешенный момент М_G = – R r (рис. 1.35).

При кинематическом и силовом анализе стреловых систем удобно пользоваться выражениями для кинематических передаточных функций первого порядка (аналогов передаточных отношений). Одна из основных функций любого механизма – воспроизведение заданных движений, точная реализация которых была бы возможна лишь в таком абстрактном механизме, в котором звенья не деформируются, отсутствуют зазоры и погрешности изготовления. Если такой механизм имеет одну степень свободы, то положение любого звена однозначно определяется координатой (угловой или линейной) ведущего звена.

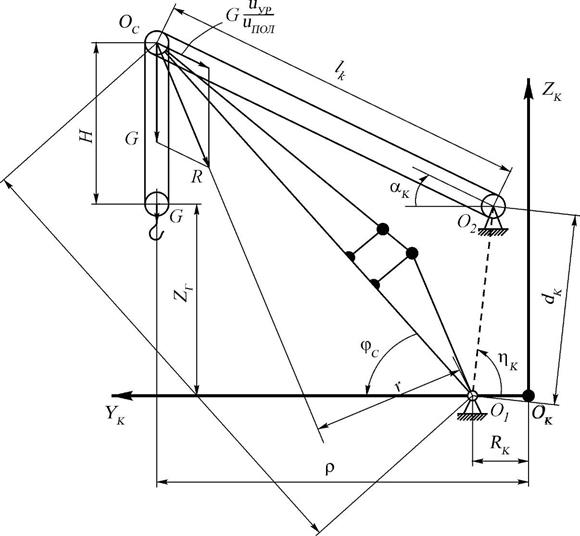
Рис. 1.37. Схема прямой стрелы с уравнительным полиспастом

Функцией положения (кинематической передаточной функцией нулевого порядка) в механизмах с одной степенью свободы называется функциональная зависимость между обобщенными координатами (угловыми или линейными) выходного и входного звеньев. Первая производная функции положения по обобщенной координате называется кинематической передаточной функцией первого порядка, вторая производная — кинематической передаточной функцией второго порядка и т.д. Кинематические передаточные функции первого и далее порядков могут быть безразмерными, а могут иметь размерности длины или длины в минус первой степени.

Кинематические передаточные функции (КПФ) не зависят от закона движения входного звена и являются собственными характеристиками механизма, так как при данном значении обобщенной координаты они зависят только от параметров кинематической схемы. Если КПФ первого порядка механизма величина постоянная, то такие механизмы называются механизмами с линейной функцией положения (например, зубчатые механизмы с постоянным передаточным отношением), в противном случае — механизмами с нелинейной функцией положения.

Рассмотрим стреловое устройство с канатом, показанное на рис. 1.37, как механизм с одной степенью свободы. За обобщенную координату примем угол j_С наклона стрелы, положительное направление которого показано на рис. 1.37. Связь между углом наклона стрелы j_С и вылетом крана r, находящимся в диапазоне R_max £ r £ R_min, задается зависимостью

r=R_K + l_C cosj_C. (1.30)

Координата Z_Гцентра масс груза определяется по зависимости вида

Z_Г = l_C sinj_C – H,(1.31)

где Н – длина подвеса груза,

Н = Н_O + Н_ПЕР,(1.32)

гдеН_O – начальная длина подвеса груза, Н_ПЕР — изменение длины подвеса груза за счет перекатывания грузовых канатов при работе механизма изменения вылета.

Величину Н_ПЕР для прямой стрелы с уравнительным полиспастом по схеме на рис. 1.37 найдем из следующих соображений. При неработающем механизме подъема общая длина L_К грузового каната остается постоянной и может быть записано равенство

L_К = (H_O + H_ПЕР) u_ПОЛ + l_К u_УР (1.33)

где l_К—длина уравнительного полиспаста. Продифференцировав по времени равенство (1.33), получим

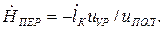
Введем в рассмотрение КПФ u_K , определяемое по формуле

(1.34)

Из треугольника О₁ О₂ О_C на рис. 1.33 найдем l_К в виде

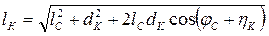(1.35)

На основании анализа формулы (1.31) с учетом выражений (1.32) и (1.35) следует сделать вывод, что для прямых стрел с уравнительным полиспастом принципиально невозможно получить одно и то же значение Z_Г на всех вылетах (при любом угле j_C), поскольку слагаемые в формуле (1.31) изменяются по качественно разным законам. Возможно лишь приближенное выполнение условия Z_Г = const.

Дифференцируя по времени соотношение (1.35), получим

u_К = – u_УР l_С d_К sin(j_С + h_К) / u_ПОЛ l_К, (1.36)

где l_K определяется по (1.35).

Введем в рассмотрение еще две КПФ первого порядка:

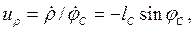(1.37)

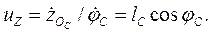(1.38)

Здесь 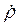и 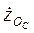представляют собой соответственно горизонтальную и вертикальную проекции абсолютной скорости конца стрелы (точки О_С) на соответствующие оси координат.

Теперь в соответствии с (1.31) КПФ первого порядка

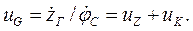(1.39)

Тогда в соответствии с (1.29) грузовой неуравновешенный момент

M_G = G u_G. (1.40)

Изменение кординаты Z_Г в зависимости от угла наклона стрелы j_С:

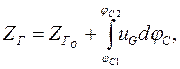(1.41)

где 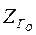– начальное значение координаты Z_Г.

Использование выражений для КПФ первого порядка значительно упрощает расчет системы изменения вылета портальных кранов, что особенно проявляется для кранов с шарнирно-сочлененной стреловой системой (см. далее), и позволяет эффективней использовать ЭВМ. Так, если к концу стрелы приложена сила F_a, то момент относительно корня стрелы этой силы M_a = F_a u_r..

Определение параметров прямой стрелы с уравнительным полиспастом производится следующим образом. Длина стрелы l_С определяется в зависимости от наибольшего вылета R_max и высоты расположения конца стрелы над ее корнем на наибольшем вылете, указываемых в задании на проектирование. Отношение кратностей u_УР / u_ПОЛ рекомендуется принимать равным трем. При меньших значениях нельзя получить удовлетворительную траекторию груза и кривую грузового неуравновешенного момента, а принятие отношения u_УР / u_ПОЛ> 3нецелесообразно, поскольку улучшение траектории груза и кривой M_G не окупается усложнением стрелового устройства. Таким образом, задача сводится к определению координат d_Kи h блока О₂ (рис. 1.37).

Решение задачи зависит от критерия, принимаемого при оптимизации параметров стреловой системы. Если таким критерием считать отклонение DZ_Г траектории груза от горизонтали, то минимум DZ_Г достигается при равенстве друг другу ординат груза при наибольшем Z_Г1 и наименьшем Z_Г2вылетах [15]. Тогда на основании формул (1.31), (1.33), (1.35) можно записать соотношения

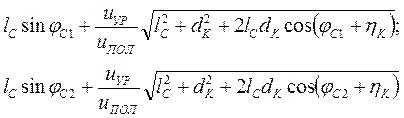, (1.42)

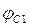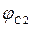где и — значения угла j_С наклона стрелы на наибольшем R_max и наименьшем R_min вылетах.

Задаваясь значениями угла h_К, можно найти значения d_К, решая уравнение численно. Меньшее отклонение траектории DZ_Г получается при больших значениях угла h_К; поскольку значения угла h_К > 90^◦ неконструктивны (наклон колонны в сторону увеличения вылета), наилучшим является h_К =90^◦.

Для качественного анализа положим j_С1 = 0, j_С2 = 90^◦, h_К = 90^◦. Тогда уравнение (1.42) примет вид

,

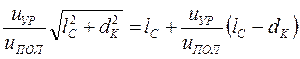откуда отношение .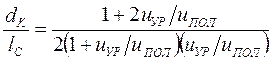

Если 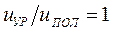, то 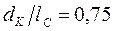; если же , то 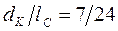. Таким образом, применение уравнительного полиспаста обеспечивает равные ординаты груза на граничных вылетах при значительно меньшей высоте колонны.

Более правильно при определении параметров прямой стрелы исходить из характеристик грузового неуравновешенного момента. Если момент М_G во всем диапазоне изменения вылета имеет малые значения, то можно быть уверенным в приемлемости траектории груза; обратное утверждение не всегда справедливо. Грузовой неуравновешенный момент М_G в соответствии с (1.40) пропорционален весу груза G и u_G.КПФ u_G для этого случая удобно представить в виде

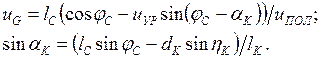(1.43)

где a_K– угол наклона оси канатов уравнительного полиспаста (см. рис.1.37).

Если принять на наибольшем вылете 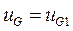,а на наименьшем 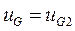то получим два уравнения:

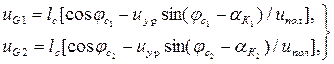
откуда определяются граничные по вылету значения углов 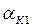и 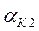. Отвечающее им положение блоков О₂ уравнительного полиспаста (значения d_K и h_K) находим из решения системы уравнений вида (1.43) или графическим путем [15].

Менее распространенные конструкции прямых стрел с уравнительным полиспастом описаны в литературе [5].

Представляет интерес прямая стрела с разнесенными блоками уравнительного полиспаста (рис. 1.38), когда 2/3 блоков (при u_УР / u_ПОЛ = 3) находятся на кронштейне О₆, а одна треть на конце стрелы О_С.

Это позволяет обеспечить более конструктивную форму конца стрелы, что особенно важно для кранов большой грузоподъемности. В этом случае M_G = R₁ r₁ – R₂ r_2. Грузовой неуравновешенный момент M_G для прямых стрел по схеме на рис. 1.38 определяется по формуле (1.40), u_G — по (1.39), u_Z — по (1.38). Для определения КПФ первого порядка u_К воспользуемся тем же методом, что и для прямых стрел с совмещенными блоками уравнительного полиспаста. В этом случае общая длина L_К каната, запасованного в полиспасты (рис. 1.38), определяется по формуле

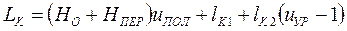. (1.44)

Продифференцировав по времени соотношение (1.44), получим

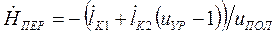. (1.45)

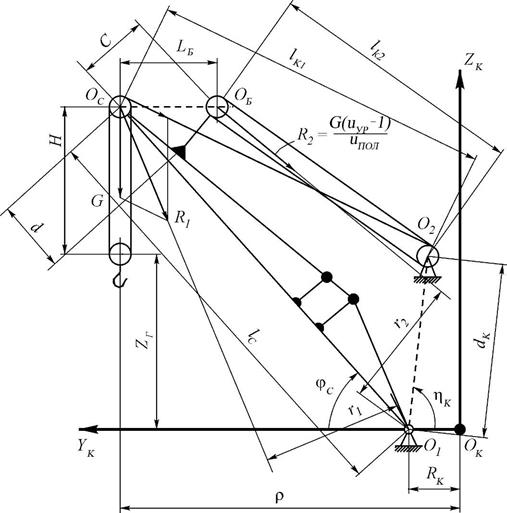
Рис. 1.38. Схема прямой стрелы с разнесенными блоками уравнительного

полиспаста

Величины 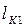и 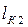найдем в соответствии со схемой на рис. 1.34 в виде

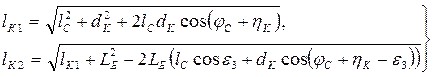, (1.46)

где ; .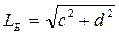

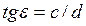Используя выражения (1.45), (1.46), получим выражение для u_К:

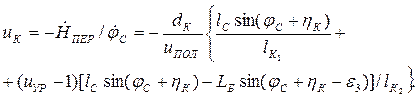(1.47)

Координаты оси О₂ блоков для таких стрел в зависимости от характера грузового неуравновешенного момента определяются следующим образом. Длину стрелы l_С назначают исходя из задания на проектирование (с учетом размещения груза под стрелой при минимальном вылете), кратность u_ПОЛгрузового полиспаста — в зависимости от грузоподъемности крана. Далее задаются кратностью уравнительного полиспаста и координатами си dблоков на стреле (предпочтительней меньшие значения для снижения дополнительного нагружения стрелы изгибающим моментом). Тогда остаются неизвестными параметры d_Ки h_К, которые определяются из условия равенства грузовых неуравновешенных моментов на граничных вылетах. Задача решается с применением ЭВМ [15].

Прямые стрелы с уравнительным блоком в современных конструкциях портальных кранов не используются вследствие сложной конструкции рычажной системы; их схемы можно найти в литературе [5].