Минимизация затрат, необходимых для сокращения времени реализации проекта (второй способ)
Обозначения:
(i, j) — работа проекта в соответствии с определениями, данными в теме 7;
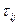 — нормальная продолжительность работы (i,j) (продолжительность работы при детерминированном подходе — метод СРМили ожидаемое время выполнения работы при стохастическом подходе — метод PERT);
— нормальная продолжительность работы (i,j) (продолжительность работы при детерминированном подходе — метод СРМили ожидаемое время выполнения работы при стохастическом подходе — метод PERT);
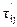 — продолжительность работы (i,j) при максимально возможном ее сокращении;
— продолжительность работы (i,j) при максимально возможном ее сокращении;
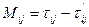 - величина максимально возможного сокращения продолжительности работы (i,j) за счет дополнительных ресурсов;
- величина максимально возможного сокращения продолжительности работы (i,j) за счет дополнительных ресурсов;
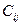 — расчетные затраты на выполнение работы (i,j) при нормальной ее продолжительности;
— расчетные затраты на выполнение работы (i,j) при нормальной ее продолжительности;
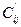 — расчетные затраты на выполнение работы (i,j) в условиях максимального сокращения ее продолжительности за счет дополнительных ресурсов;
— расчетные затраты на выполнение работы (i,j) в условиях максимального сокращения ее продолжительности за счет дополнительных ресурсов;
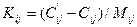 - удельные затраты на сокращение продолжительности работы (i,j) (на единицу времени).
- удельные затраты на сокращение продолжительности работы (i,j) (на единицу времени).
Предположим, что любая дополнительная доля сокращаемого времени на выполнение работы потребует постоянной (неизменной во времени) доли дополнительных затрат. При таком предположении для минимизации затрат на сокращение времени реализации проекта можно использовать модель линейного программирования.
Для формулировки модели дополнительно введем следующие обозначения:
P- множество работ проекта;
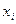 — время наступления события i (событие-узел отражает факт завершения всех работ, входящих в данный узел);
— время наступления события i (событие-узел отражает факт завершения всех работ, входящих в данный узел);
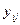 - величина сокращения времени работы (i, j);
- величина сокращения времени работы (i, j);
i = 1 —номер начального события для сети, описывающей проект;
i = п —номер конечного события для сети, описывающей проект;
T0 — желательное время выполнения проекта.
При данных обозначениях модель линейного программирования имеет вид
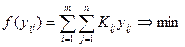 , (7.10.1)
, (7.10.1)
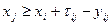 , (7.10.2)
, (7.10.2)
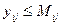 , (7.10.3)
, (7.10.3)
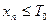 , (7.10.4)
, (7.10.4)
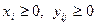 , (7.10.5)
, (7.10.5)
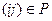 .
.
Если т — число работ, п — число событий, то описанная модель имеет п + т переменных, т ограничений (7.10.2), т ограничений (7.10.3), п + т ограничений (7.10.5) и одно ограничение (7.10.4). Итого п + т переменных и 3т + n + 1 ограничение.
Если {xj*, уij*} — оптимальный план, полученный для модели (710.1)—(7.10.5), то уij* — время, на которое следует сократить продолжительность выполнения работы (i,j); 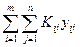 — минимальная сумма издержек, необходимая для сокращения времени выполнения проекта до T0.
— минимальная сумма издержек, необходимая для сокращения времени выполнения проекта до T0.
2. Метод анализа затрат PERT/COST. Метод основан на построении области допустимых затрат, при которых проект может быть реализован за определенное время. В результате применения метода СРМили метода PERTможет быть получено наиболее раннее и наиболее позднее время начала каждой работы. Далее строятся два графика: график совокупных затрат при наиболее раннем времени начала работ и график совокупных затрат при наиболее позднем времени начала работ.
Если фактические затраты на выполнение проекта будут находиться внутри области, очерченной этими графиками, то проект может быть выполнен за время, соответствующее длине критического пути. Если фактические затраты окажутся за пределамиочерченной области, то продолжительность выполнения проекта увеличится.
Пример 2. Минимизация затрат на сокращение времени реализации проекта. Проект пуско-наладки компьютерной системы состоит из восьми работ. В таблице 7.1 указаны взаимосвязь работ, нормальное время их выполнения и данные, характеризующие возможность сокращения продолжительности работ:
Таблица 7.1
| Работа | Опорные работы | Время выполнения, недели | Затраты, руб., при времени выполнения | Прирост затрат, руб., на один день ускорения работ | ||
Нормаль-ное 
| мини-маьное 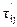
| нормаль-ное 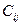
| минималь-
ное 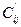
| |||
| A | - | |||||
| B | - | |||||
| C | A | |||||
| D | B,C | |||||
| E | D | |||||
| F | E | |||||
| G | B,C | |||||
| H | F,G |
Определите минимальную продолжительность проекта при нормальном времени выполнения работ. Можно ли уменьшить продолжительность проекта при дополнительных затратах?
Вопросы:
1. Какова продолжительность проекта при нормальном времени выполнения работ?
2. Сколько работ в этом случае являются критическими?
3. Каковы затраты на выполнение проекта при нормальном времени выполнения работ?
4. С какими минимальными дополнительными затратами можно выполнить этот проект за 16 недель?
Решение. Первый способ. Найдем критический путь при нормальном времени выполнения работ. Используем для этого метод СРМ.

Рис.7.2. Сетевой график для примера 2
Определяем критической путь.
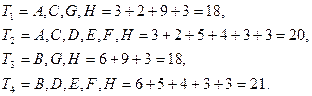
Отсюда видно, что при нормальной продолжительности работ длина критического пути составляет 21 неделю. На критическом пути находятся работы В, D, Е, F, Н. Для того чтобы определить затраты на выполнение проекта при нормальной продолжительности работ, достаточно просуммировать затраты, указанные в пятом столбце таблицы исходных данных. В результате получаем затраты 18 700 руб.9300
Для определения минимальных дополнительных издержек, необходимых для того, чтобы снизить продолжительность проекта до 16 недель, построим модель линейного программирования. Для этого на основании данных о непосредственно предшествующих работах построим графическое представление проекта (рис. 7.2).
Используя исходные данные (таблица 7.1) и формулы 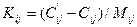 и
и 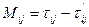 определяем удельные (в единицу времени) затраты Кij на сокращение продолжительности работ. Получаем следующие результаты:
определяем удельные (в единицу времени) затраты Кij на сокращение продолжительности работ. Получаем следующие результаты:
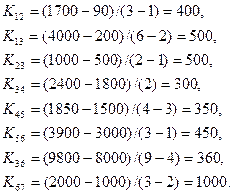
Используя обозначения хi — время наступления события i, 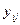 - величина сокращения времени работы (i,j), получаем следующую модель линейного программирования для определения минимальных издержек, необходимых для сокращения продолжительности проекта с 21 до 16 недель:
- величина сокращения времени работы (i,j), получаем следующую модель линейного программирования для определения минимальных издержек, необходимых для сокращения продолжительности проекта с 21 до 16 недель:
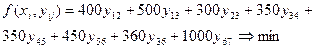
при условиях
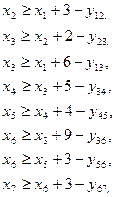
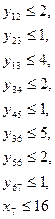
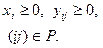 или
или 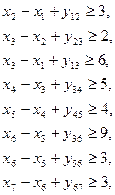
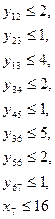
Для решения сформулированной задачи можно использавать или программу Solver (поиск решения).
В следующей таблице приведенная выше модель представлена в формате программы поиск решения:
| п/п | x1 | x2 | x3 | x4 | x5 | x6 | x7 | y12 | y13 | y23 | y34 | y45 | y56 | y36 | y67 | лчо | во | пчо |
| пп | ||||||||||||||||||
| -1 | >= | |||||||||||||||||
| -1 | >= | |||||||||||||||||
| -1 | >= | |||||||||||||||||
| -1 | >= | |||||||||||||||||
| -1 | >= | |||||||||||||||||
| -1 | >= | |||||||||||||||||
| -1 | >= | |||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= |
Выполнив расчеты, получаем следующие результаты:
| п/п | x1 | x2 | x3 | x4 | x5 | x6 | x7 | y12 | y13 | y23 | y34 | y45 | y56 | y36 | y67 | лчо | во | пчо |
| пп | ||||||||||||||||||
| -1 | >= | |||||||||||||||||
| -1 | >= | |||||||||||||||||
| # | >= | |||||||||||||||||
| -1 | >= | |||||||||||||||||
| -1 | >= | |||||||||||||||||
| -1 | >= | |||||||||||||||||
| -1 | >= | |||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= | ||||||||||||||||||
| <= |
Итак, минимальные затраты, необходимые для того, чтобы сократить продолжительность проекта с 21 до 16 недель, составляют 7950 руб.
Продолжительность каждой из работ (1, 3), (4, 5), (5, 6) и (3, 6) сокращается на одну неделю. Продолжительность работы (3, 4) сокращается на две недели.
Ответы: 1. 21 неделя. 2. Пять работ. 3. 18 700 руб. 4. 2260 руб.
Пример 2. Контроль затрат на выполнение проекта.
Перечень работ проекта, время их выполнения и оценки затрат на выполнение работ отражены в следующей таблице:
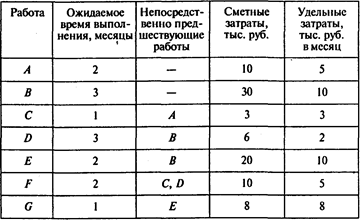
Удельные затраты определены в предположении о том, что затраты производятся равномерно в течение срока выполнения работы.
Определите, в каком диапазоне могут меняться фактические затраты на выполнение проекта при условии, что проект будет выполнен за минимальное время.
Вопросы:
1. За какое минимальное время может быть выполнен проект?
2. При каком максимальном значении совокупных затрат, сделанных за первые 3 месяца реализации проекта, проект может быть выполнен за минимальное время?
3. При каком минимальном значении совокупных затрат, сделанных за первые 3 месяца реализации проекта, проект может быть выполнен за минимальное время?
4. При каком максимальном значении совокупных затрат, сделанных за 6 месяцев реализации проекта, проект может быть выполнен за минимальное время?
5. При каком минимальном значении совокупных затрат, сделанных за 6 месяцев реализации проекта, проект может быть выполнен за минимальное время?
Решение. Определим минимальное время выполнения проекта. Найдем критический путь, воспользовавшись методом СРМ. Введем в программу POMWIN информацию о предшествующих работах и времени их выполнения:
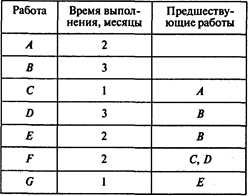
Результаты расчетов представлены в следующей таблице:
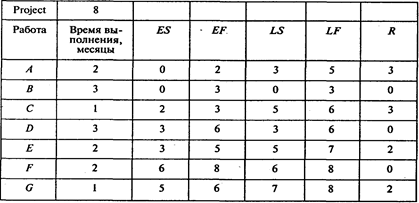
Ожидаемое время выполнения проекта равно 8 месяцам.
Определим динамику совокупных затрат для графика выполнения проекта с наиболее ранним началом всех работ:
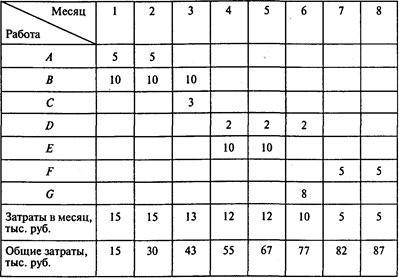
Определим динамику совокупных затрат для графика выполнения проекта с наиболее поздним началом всех работ:
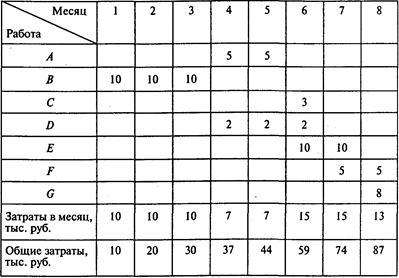
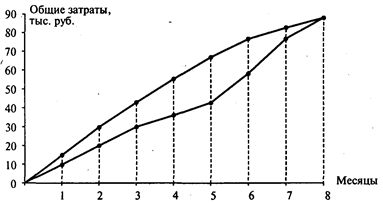
Рис. 2
На рис. 2 показаны два графика. Выше проходит график совокупных затрат при наиболее раннем времени начала работ, ниже — при наиболее позднем времени начала работ. Если фактические затраты на выполнение проекта будут находиться внутри очерченной области, то проект может быть выполнен за 8 месяцев. Если фактические затраты окажутся за пределами очерченной области, то продолжительность проекта увеличится.
Таким образом, менеджер может контролировать фактические затраты по проекту. Если сметные затраты не выполнены или допущен перерасход, необходимо осуществлять корректирующие воздействия, сдвигая время начала отдельных работ и (или) сокращая их продолжительность путем привлечения дополнительных ресурсов.
Ответы: 1. Восемь месяцев. 2. 43 тыс. руб. 3. 30 тыс. руб. 4. 77 тыс. руб. 5. 59 тыс. руб.
Вопросы
Вопрос 1. Для определения минимальных затрат, необходимых для выполнения проекта за фиксированное время, следует использовать:
1) метод СРМ;
2) метод PERT;
3) модель линейного программирования;
4) модель транспортного типа;
5) все вышеперечисленное.
Вопрос 2. Пусть в графе, описывающем проект, т работ и п событий (вершин сети). Число переменных в модели линейного программирования для определения минимальных затрат, необходимых для выполнения проекта за фиксированное время, равно:
1) т;
2) п;
3) т+ п;
4) т– п;
5) т • п.
Вопрос 3. Какую формулу следует использовать для определения величины удельных затрат Кij на сокращение продолжительности работы (i, j)?
Варианты ответов:
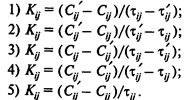
Вопрос 4. Какое из указанных далее соотношений является верным?
Варианты ответов:
1) совокупные затраты при наиболее позднем времени начала работ превышают совокупные затраты при наиболее раннем времени начала работ;
2) совокупные затраты при наиболее раннем времени начала работ превышают совокупные затраты при наиболее позднем времени начала работ;
3) совокупные затраты при наиболее раннем времени начала работ равны совокупным затратам при наиболее позднем времени начала работ;
4) совокупные затраты при наиболее раннем времени начала работ превышают совокупные затраты при наиболее позднем времени начала работ на величину сметной стоимости проекта;
5) совокупные затраты при наиболее раннем времени начала работ и совокупные затраты при наиболее позднем времени начала работ постоянны.
Вопрос 5. Для осуществления контроля за расходованием средств на выполнение проекта используется:
1) метод СРМ;
2) метод PERT;
3) модель линейного программирования;
4) все вышеперечисленное;
5) метод PERT/COST.
Задачи
Задача 1. Рассмотрите следующую сеть проекта с показателями продолжительности работ (в неделях) и информацией о затратах на сокращение продолжительности работ (в тыс. руб.) за счет привлечения дополнительных финансовых средств:
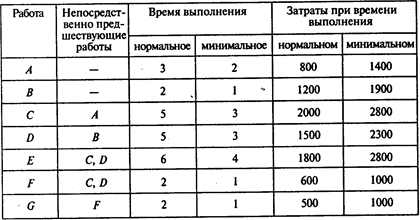
Найдите критический путь и затраты на реализацию проекта при нормальном времени выполнения всех работ.
Предположим, что руководство хотело бы завершить проект в 10-недельный срок. Постройте модель линейного программирования, которую можно было бы использовать для того, чтобы определить минимальные затраты на сокращение времени выполнения проекта.
Вопросы:
1. Какова продолжительность проекта при нормальном времени выполнения работ?
2. Каковы затраты на выполнение проекта при нормальной продолжительности работ?
3. Чему равны минимальные затраты на выполнение проекта в 10-недельный срок?
4. Для какого количества работ необходимо сократить время выполнения, чтобы завершить проект за 10 недель?
Задача 2.В следующей таблице представлена информация о продолжительности работ проекта (в месяцах) и затратах на их выполнение (в тыс. руб.):
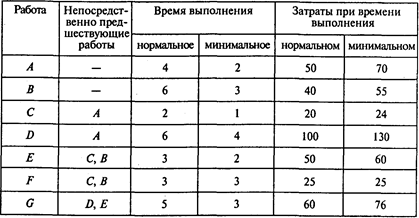
Найдите критический путь и продолжительность проекта при нормальном времени выполнения работ.
Вопросы:
1. Какова продолжительность проекта при нормальном времени выполнения работ?
2. Каковы затраты на выполнение проекта при нормальной продолжительности работ?
3. Чему равны минимальные затраты на выполнение проекта за один год?
4. За какое минимальное время может быть выполнен проект?
Задача 3. Отдел ЭВМ экономического факультета МГУ разработал предложения по внедрению новой компьютерной системы для нужд администрации факультета. В предложения включен перечень работ, которые необходимо выполнить, чтобы ввести систему в действие. Соответствующая информация представлена в следующей таблице (время — в неделях, затраты — в тыс. руб.):
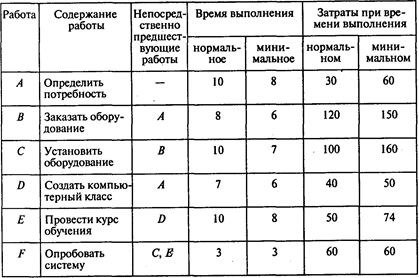
Вопросы:
1. Какова продолжительность проекта при нормальном времени выполнения работ?
2. Каковы затраты на выполнение проекта при нормальной продолжительности работ?
3. Чему равны минимальные затраты на выполнение проекта за 26 недель?
4. За какое минимальное время может быть выполнен проект?
Задача 4. Конструкторское бюро Московского часового завода (МЧЗ) разработало новый настольный радиобудильник. По мнению проектировщиков, запуск в серию нового продукта позволит расширить рынок сбыта и получить дополнительную прибыль.
Руководство МЧЗ решило изучить возможности реализации нового продукта. Результатом исследования должны стать рекомендации относительно действий, которые следует предпринять для организации производства и сбыта нового продукта.
Перечень работ, время, необходимое для их выполнения (в неделях), и затраты (в тыс. руб.) указаны в следующей таблице:
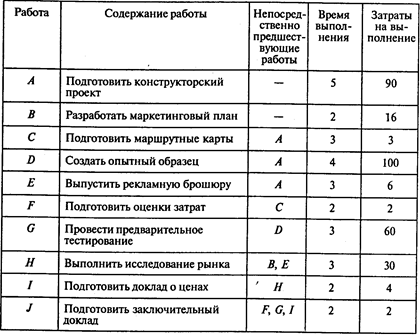
Определите критический путь для данного проекта, наиболее раннее и наиболее позднее время начала каждой работы. Определите динамику роста общих затрат на проект, основанную на данных о наиболее раннем и наиболее позднем времени начала работ.
Используйте полученные оценки сметных расходов для контроля за фактическим расходованием средств. Предполагается, что все работы финансируются пропорционально времени их выполнения.
Вопросы:
1. За какое минимальное время может быть выполнен проект?
2. Чему равно максимальное значение совокупных затрат на конец пятой недели, при котором проект может быть выполнен за время, соответствующее длине критического пути?
3. Чему равно минимальное значение совокупных затрат на конец пятой недели, при котором проект может быть выполнен за время, соответствующее длине критического пути?
4. Какова величина недостатка или перерасхода средств в конце пятой недели, если фактические затраты в этот момент составили 100 тыс. руб.?
5. Какова величина недостатка средств в конце десятой недели, если фактические затраты в этот момент составили 230 тыс. руб.?
Задача 5. Ниже представлена сеть проекта, а также данные о времени выполнения работ (в неделях) и затратах (в тыс. руб.):
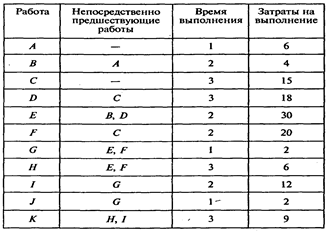
Определите критический путь для данного проекта, наиболее раннее и наиболее позднее время начала каждой работы. Определите динамику роста общих затрат на проект, основанную на данных о наиболее раннем и наиболее позднем времени начала работ.
Используйте полученные оценки сметных расходов для контроля за фактическим расходованием средств. Предполагается, что все работы финансируются пропорционально времени их выполнения.
Вопросы:
1. За какое минимальное время может быть выполнен проект?
2. Чему равно максимальное значение совокупных затрат на конец четвертой недели, при котором проект может быть выполнен за время, соответствующее длине критического пути?
3. Чему равно минимальное значение совокупных затрат на конец четвертой недели, при котором проект может быть выполнен за время, соответствующее длине критического пути?
4. Какова величина недостатка или перерасхода средств в конце четвертой недели, если фактические затраты в этот момент составили 35 тыс. руб.?
5. Какова величина недостатка средств в конце восьмой недели, если фактические затраты в этот момент составили 90 тыс. руб.?
Дата добавления: 2015-02-19; просмотров: 2579;
