Резонанс напряжений и резонанс токов

Как следует из приведенных формул, при частоте переменной ЭДС ω, равной

,

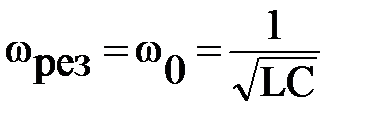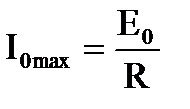амплитудное значение силы тока в колебательном контуре, принимает максимальное значение . При этом амплитуда напряженияна активном сопротивлении R также максимальнаи равна U_R0 =I_0maxR =E₀. Падения напряжения на емкости U_C и индуктивности U_L одинаковы по амплитуде, но противоположны по фазе, и они взаимно компенсируют друг друга. Это явление, имеющее место в последовательномколебательном контуре, называется резонансом напряжений. Векторная диаграмма, соответствующая этому случаю, показана на рис.4.7.

Максимальное значение амплитуды напряжения на конденсаторе U_C0(ω) достигается при частоте

.

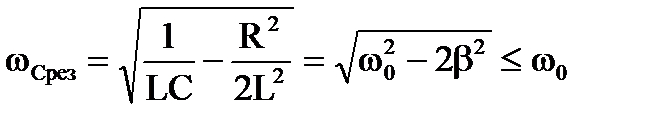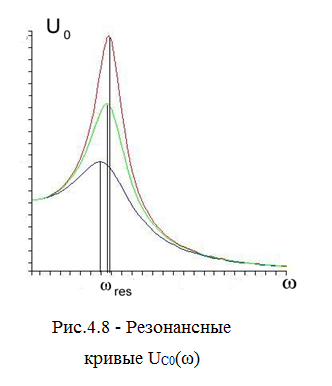Резонансные кривые для U_C0(ω) представлены на рис.4.8. Максимум получается тем выше и острее, чем меньше коэффициент затухания β, то есть чем меньше активное сопротивление и больше индуктивность контура.

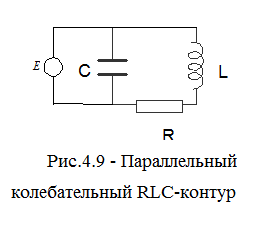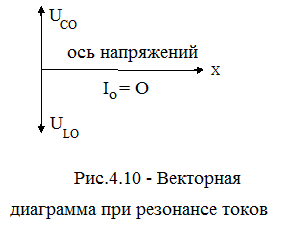
Если источник переменной ЭДС подключить параллельно конденсатору, то получим колебательный контур, который называется параллельным(рис.4.9). В таком контуре при 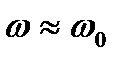наблюдается другое резонансное явление, получившее название резонанса токов. При резонансе токов токи, текущие через емкость и индуктивность одинаковы по амплитуде, но противоположны по фазе. При этом общий ток в цепи ЭДС близок к нулю, хотя токи в самом контуре могут быть очень велики. Векторная диаграмма, соответствующая этому случаю, приведена на рис.4.10. Можно показать, что при резонансе токов полное сопротивление Z(ω) параллельного контура максимально и равно чисто активному сопротивлению R. Резонансная частота, при которой Z(ω) максимально, определяется из условия равенства нулю реактивной части комплексного сопротивления

:

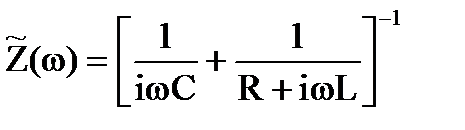ωL(1 – ω²LC) – ωCR² = 0 ,

откуда

.

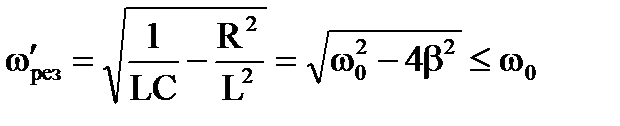Резонансные кривые для амплитудных значений I_C0(ω) тока, текущего через конденсатор, приведены на рис. 4.11. Резонансные явления в коле 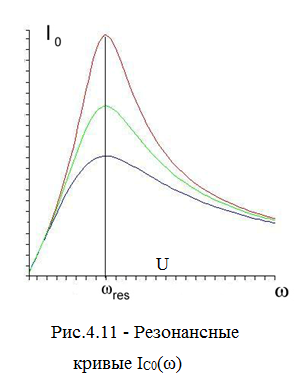бательных контурах широко используются в электро- и радиотехнике (резонансные усилители, частотные фильтры и другие). В частности, явление резонанса используется для выделения из сложного сигнала нужной частотной составляющей. Настроив контур (путем изменения его параметров C и/или L) на одну из выбранных частот, можно получить на конденсаторе напряжение, в Q раз превышающее величину напряжения данной частотной составляющей (см. рис.4.8). Такой процесс осуществляется, например, при настройке радиоприемника на нужную длину волны.

Контрольные вопросы первого уровня

1. Из каких элементов состоит колебательный контур для создания свободных гармонических колебаний? Запишите закон Ома для этого контура.

2. Чему равна частота свободных колебаний? По какой формуле определяется период?

3. Как различаются по фазе колебания заряда, силы тока и разности потенциалов? Нарисуйте графики.

4. Почему происходит затухание колебаний при добавлении в колебательный контур сопротивления? Запишите закон Ома для этого контура.

5. Как изменяется со временем амплитуда затухающих колебаний? Как определяется частота затухающих колебаний?

6. Что называется логарифмическим декрементом затуханий? Какова его взаимосвязь с периодом и коэффициентом затуханий?

7. Что называется добротностью? Какова связь между добротностью и потерями энергии в колебательном контуре?

8. Из каких элементов состоит колебательный контур для создания вынужденных колебаний? Запишите закон Ома для этого контура.

9. Что называется резонансом? Каково условие наступления резонанса напряжений и резонанса токов?

10. Проведите анализ резонансных кривых.

Методические указания по решению задач

Во многих задачах данного раздела удобно использовать закон сохранения энергии. Этому закону следует придать форму, связывающую амплитудные и текущие значения напряжения, заряда или тока в отдельных элементах схемы.

Цель:В задачах этого параграфа рассматриваются гармонические (собственные и вынужденные) и затухающие электромагнитные колебания.