Примеры решения задач. Задача 1.В колебательном контуре с индуктивностью и емкостью конденсатор заряжен до максимального напряжения
Задача 1.В колебательном контуре с индуктивностью  и емкостью
и емкостью 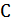 конденсатор заряжен до максимального напряжения
конденсатор заряжен до максимального напряжения 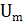 . Каким будет ток
. Каким будет ток 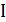 в контуре в тот момент, когда напряжение на конденсаторе уменьшится в два раза? Колебания считать незатухающими.
в контуре в тот момент, когда напряжение на конденсаторе уменьшится в два раза? Колебания считать незатухающими.
Решение: В отсутствии затухания суммарная энергия электрического и магнитного полей в контуре сохраняется. Следовательно, в каждый момент времени справедливо равенство:
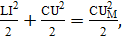 откуда
откуда 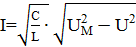
По условию задачи 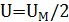 . Ток в контуре в этот момент времени равен:
. Ток в контуре в этот момент времени равен: 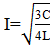 .
.
Задача 2.В колебательном контуре конденсатору с емкостью 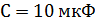 сообщили заряд
сообщили заряд 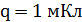 , после чего возникли затухающие электромагнитные колебания. Сколько тепла
, после чего возникли затухающие электромагнитные колебания. Сколько тепла 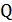 выделится к моменту, когда максимальное напряжение на конденсаторе станет меньше максимального напряжения в
выделится к моменту, когда максимальное напряжение на конденсаторе станет меньше максимального напряжения в 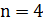 раза?
раза?
Решение: Количество выделившегося тепла равно разности между начальными и конечными значениями энергии в контуре. В моменты, когда напряжение на конденсаторе максимально, ток через катушку равен нулю. Следовательно, энергия в эти моменты сосредоточена в конденсаторе. Имеем:
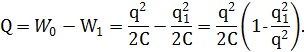
Учитывая, что 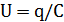 и в интересующий нас момент времени
и в интересующий нас момент времени 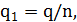 получаем ответ:
получаем ответ:
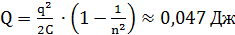 .
.
Задача 3. Катушка индуктивностью 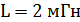 с сопротивлением обмотки
с сопротивлением обмотки 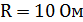 и конденсатора емкостью
и конденсатора емкостью 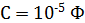 подключены параллельно к источнику ЭДС
подключены параллельно к источнику ЭДС 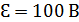 и внутренним сопротивлением
и внутренним сопротивлением 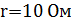 . Какое количество тепла
. Какое количество тепла 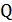 выделится в контуре после отключения источника?
выделится в контуре после отключения источника?
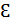
|
| r |
| C |
| L |
| R |
| Рисунок 4.12 – К задаче 3 |
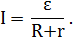
Напряжение на конденсаторе, равное напряжению на катушке, будет:
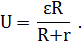
Суммарная энергия заряженного конденсатора и катушки с током:
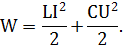
После отключения источника в контуре, состоящем из катушки и конденсатора, возникнут затухающие электромагнитные колебания, в результате которых вся начальная энергия перейдет в тепло:
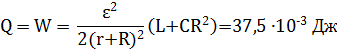
Задача 4.Конденсатор емкостью 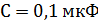 , заряженный до напряжения
, заряженный до напряжения 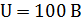 , подсоединяют катушку индуктивности
, подсоединяют катушку индуктивности 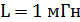 . Чему равна величина тока
. Чему равна величина тока 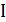 через катушку спустя время
через катушку спустя время 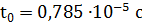 после подключения конденсатора? Сопротивлением катушки и соединительных проводов пренебречь.
после подключения конденсатора? Сопротивлением катушки и соединительных проводов пренебречь.
Решение: При подключении заряженного конденсатора к катушке в образовавшемся контуре возникают электрические колебания с частотой 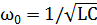 . При этом заряд на конденсаторе меняется во времени по закону:
. При этом заряд на конденсаторе меняется во времени по закону:
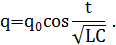
где 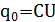 - начальный заряд на конденсаторе. Поскольку сопротивление катушки и соединительных проводов пренебрежимо мало, суммарная энергия электрического и магнитного поля в контуре сохраняется. Из закона сохранения энергии следует, что:
- начальный заряд на конденсаторе. Поскольку сопротивление катушки и соединительных проводов пренебрежимо мало, суммарная энергия электрического и магнитного поля в контуре сохраняется. Из закона сохранения энергии следует, что:
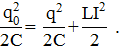
Выражая отсюда ток через катушку, имеем:
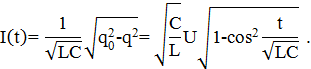
Величина тока в момент времени 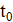 равна:
равна:
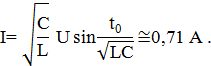
Задача 5.Колебательный контур состоит из катушки индуктивности и четырех конденсаторов, соединенных как показано на рисунке. Во сколько раз  изменится период собственных колебаний в контуре, если замкнуть ключ, соединяющий точки А и
изменится период собственных колебаний в контуре, если замкнуть ключ, соединяющий точки А и  ?
? 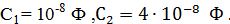
| L |
| C |
| C |
| C |
| C |
| A |
| B |
| Рисунок 4.13 – К задаче 5 |
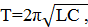 отношение периода
отношение периода 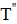 колебаний после замыкания ключа к периоду
колебаний после замыкания ключа к периоду 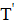 колебаний до замыкания ключа выразится как:
колебаний до замыкания ключа выразится как:
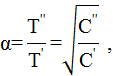
где 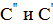 - емкости батареи конденсаторов в этих двух случаях соответственно. Расчет по стандартным формулам дает:
- емкости батареи конденсаторов в этих двух случаях соответственно. Расчет по стандартным формулам дает:
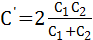 при разомкнутом ключе,
при разомкнутом ключе,
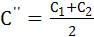 при замкнутом ключе.
при замкнутом ключе.
Отсюда получаем ответ: 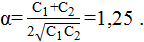
Задача 6.В цепи, показанной на рисунке, конденсатор емкостью 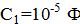 вначале заряжен до напряжения
вначале заряжен до напряжения 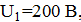 а конденсатор емкостью
а конденсатор емкостью 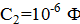 разряжен. До какого максимального значения
разряжен. До какого максимального значения 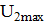 может зарядиться конденсатор
может зарядиться конденсатор 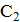 в процессе колебаний, возникающих в цепи после замыкания ключа? Потерями в соединительных проводах и в катушке индуктивности пренебречь.
в процессе колебаний, возникающих в цепи после замыкания ключа? Потерями в соединительных проводах и в катушке индуктивности пренебречь.
| K |
| L |
| C |
| C |
| U |
| Рисунок 4.14 – К задаче 6 |
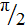 . В момент достижения максимального напряжения на конденсаторах ток в цепи обратится в нуль, следовательно, вся энергия будет сосредоточена на конденсаторах. При этом на конденсатор
. В момент достижения максимального напряжения на конденсаторах ток в цепи обратится в нуль, следовательно, вся энергия будет сосредоточена на конденсаторах. При этом на конденсатор 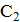 перетечет из конденсатора
перетечет из конденсатора 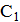 некоторый заряд
некоторый заряд 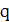 , а на конденсаторе
, а на конденсаторе 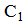 останется заряд
останется заряд 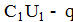 . Величину заряда
. Величину заряда 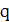 на конденсаторе
на конденсаторе 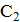 можно найти из закона сохранения энергии в контуре. В силу того, что в рассматриваемый момент времени магнитная энергия обращается в нуль,
можно найти из закона сохранения энергии в контуре. В силу того, что в рассматриваемый момент времени магнитная энергия обращается в нуль,
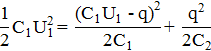
Отсюда 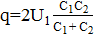 . Учитывая, что
. Учитывая, что  , получаем ответ:
, получаем ответ:
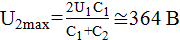 .
.
Вывод: При решении задач следует уделять внимание как общим закономерностям, присущим колебательным процессам, так и физической сущности явлений, происходящих в электрическом колебательном контуре.
Дата добавления: 2015-02-13; просмотров: 8381;
