Формула трапеции

На частичном отрезке (х_i-1, x_i) площадь криволинейной трапеции АВСД заменяется площадью прямоугольной трапеции АВСД (рис. 2).

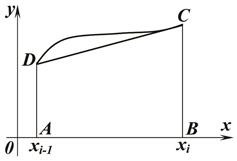
Рис. 2

Тогда

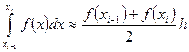
Для оценки погрешности

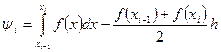
Представим его в виде

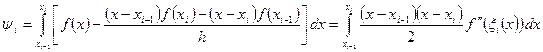
Отсюда получим

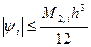
Составная формула трапеции имеет вид

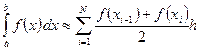
Погрешность этой формулы оценивается следующим образом:

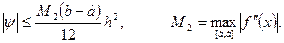
Таким образом, формула трапеции имеет вид, так же как и формула прямоугольников, второй порядок точности, 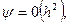но ее погрешность оценивается величиной в два раза большей.

Применение формулы трапеции или прямоугольников требует оценки второй производной 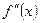на отрезке [а, в]. Если такая оценка затруднительна (или вообще невозможно, например, в случае функции определяемых опытным путем), то в предположений малого изменения (или монотонности) второй производной 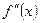можно во всех полученных оценках заменить множителя М₂h² наибольшей величиной

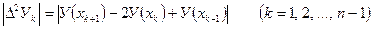
Отсюда видно, что формула прямоугольников и трапеции дает достаточную точность только при достаточно малых разностях второго порядка ∆²У_k (а именно, когда произведения 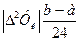не превосходят допустимой погрешности расчета).

Для уточнения величины интеграла можно использовать, то обстоятельство, что с уменьшением шага h в два раза погрешность формулы трапеций уменьшается примерно в четыре раза. Отсюда следует, что совпадающие знаки в значениях интеграла, вычисленных с шагом h и можно считать верным. Действительно, если погрешность значения интеграла, вычисленного с шагом обозначить через ε, то погрешность значения интеграла, вычисленного с шагом h, будет приближенно равна 4ε, и значить, разность указанных значений интеграла будет не менее чем 3ε. Поэтому из совпадения m десятичных знаков у рассматриваемых значений интеграла можно заключить, что погрешность 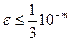, а это означает, что в значений интеграла вычисленном с шагом 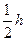, все m десятичных знаков верны (здесь предполагается, что погрешность исходных данных пренебрежимо мало).