Решение задачи 2
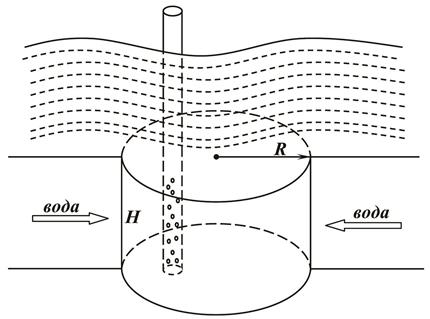
Рис. 5
Для расчета изменения во времени давления на контуре нефтяной залежи, используя аппроксимацию соответствующих решений Карслоу и Егера, имеем
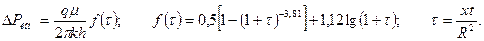
Этой формулой можно пользоваться, если приток воды из законтурной области пласта к нефтяной залежи цилиндрической формы с постоянным дебитом.
Однако, по условиям данной задачи в период разбурения месторождения объем воды, поступающей из законтурной области, и следовательно, отбираемой жидкости из пласта – переменные во времени. Поэтому для расчета давления на контуре нефтяного месторождения Pкон (t) необходимо использовать интеграл Дюамеля, согласно которому

В условиях задачи qж зависит от физического времени t. В интеграл необходимо поставить 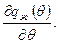 Поэтому найдем зависимость qж = qж(τ) или, что то же самое, qж = qж(λ). Имеем
Поэтому найдем зависимость qж = qж(τ) или, что то же самое, qж = qж(λ). Имеем
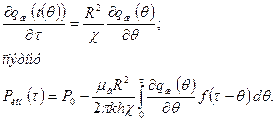
Это формула применяется в том случае, если

Задание для лабораторной работы.
| № п/п | Известные параметры | Определить | Число разбивания |
μ, k, x, H, в, tk, α0, 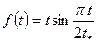 μ, k, x, H, в, tk, α0,
μ, k, x, H, в, tk, α0,  μ, k, x, H, в, tk, α0,
μ, k, x, H, в, tk, α0, 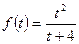 μ, k, x, H, в, tk, α0,
μ, k, x, H, в, tk, α0, 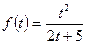 μ, k, x, H, в, tk, α0,
μ, k, x, H, в, tk, α0, 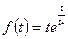 μ, k, x, H, R, tk, α0, ρ0,
μ, k, x, H, R, tk, α0, ρ0, 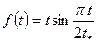 μ, k, x, H, R, tk, α0, ρ0,
μ, k, x, H, R, tk, α0, ρ0,  μ, k, x, H, R, tk, α0, ρ0,
μ, k, x, H, R, tk, α0, ρ0, 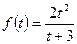 μ, k, x, H, R, tk, α0, ρ0,
μ, k, x, H, R, tk, α0, ρ0,  μ, k, x, H, R, tk, α0, ρ0,
μ, k, x, H, R, tk, α0, ρ0, 
| ΔP(t) ΔP(t) ΔP(t) ΔP(t) ΔP(t) P(t) P(t) P(t) P(t) P(t) | n=100, 200 n=200, 400 n=300, 600 n=150, 300 n=250, 500 n=300, 600 n=250, 500 n=250, 500 n=200, 400 n=500, 1000 |
Дата добавления: 2015-02-13; просмотров: 764;
