Сплайн 1-го порядка (кусочно-линейная интерполяция)
                             Точки Точки 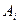 и и 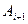 соединяются прямыми линиями, т.е. получаем ломаную линию А0, А1, А2, …, Аn
(рис. 12).Используя уравнение прямой, проходящей через точки Аi (xi, уi),
Ai+1 (xi+1 ,уi+1) получим соединяются прямыми линиями, т.е. получаем ломаную линию А0, А1, А2, …, Аn
(рис. 12).Используя уравнение прямой, проходящей через точки Аi (xi, уi),
Ai+1 (xi+1 ,уi+1) получим
| у А1 А3 А2 А0 Аn a=х0 х1 0 х2 х3 хn=b х Рис.12 |
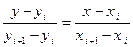 (1.1)
(1.1)
где yi = f(xi), xi = a + ih, a = x0. Из (1.1) получим
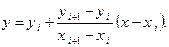 (1.2)
(1.2)
В (1.2) функция у зависит от i и х. Поэтому запишем в следующем виде
S(x)= 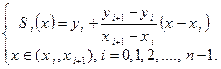 (1.3)
(1.3)
Функция (1.3) называется сплайном 1-го порядка.
Лабораторная работа. Задать самостоятельно функцию у = f(x). Составить таблицу функции у = f(x) на отрезке [а;в] в узлах хi =a+ih. Вычислить промежуточные точные значения 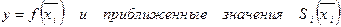 .
.
Вычислить погрешность 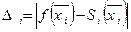 .
.
Найти среднюю арифметическую величину (мат.ожидание)
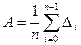
и среднеквадратическое отклонение
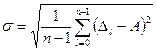 .
.
i. Переменные программирования.
Массивы.
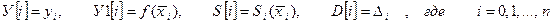
Переменные. Введем обозначения
M а= А, sig =σ , x = x,i=i .
Константы. a, b, n, h, k
Дата добавления: 2015-02-13; просмотров: 1834;
