В цепях второго порядка

Расчет переходного процесса в цепях второго порядка рассмотрим на примере простейшей цепи с последовательным соединением элементов R,L,C (рис. 6.2) при подключения ее к источнику постоянного напряжения.

Расчетная схема переходного процесса представлена на рис. 6.12.

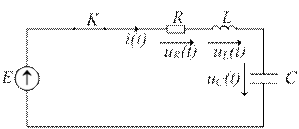
Рис. 6.12. Расчетная схема цепи второго порядка

Составляем уравнение по ЗНК для цепи после коммутации (ключ К замкнут) в соответствии с принятыми положительными направлениями тока и падений напряжения:

u_R(t)+ u_L(t) + u_C(t) = E. (6.27)

Переменными состояния, которые определяют поведение цепи в переходном процессе, являются ток i_L(t) в индуктивности и напряжение u_C(t) на емкости. Расчет переходного процесса можно вести относительно любой из переменных состояния. Характеристическое уравнение при этом получается одно и то же. Данный факт предлагается студентам проверить самостоятельно. Мы же решим уравнение (6.27) относительно тока i_L(t) в индуктивности (он же ток в цепи).

Выражая падения напряжения u_L(t) и u_R(t) через ток i_L(t) в цепи, полагая 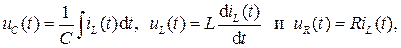получим уравнение

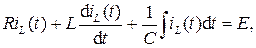
продифференцировав которое, придем к дифференциальному уравнению второго порядка:

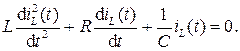(6.28)

Характеристическое уравнение имеет вид:

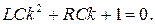
Разделив обе части уравнения на LC, получим:

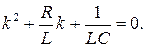
Корни уравнения:

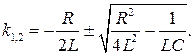(6.29)

Как было показано в разделе 6.1.2, вид решения дифференциального уравнения второго порядка зависит от вида корней характеристического уравнения. Поэтому рассмотрим два характерных случая:

− корни уравнения вещественные и разные (k₁≠ k₂);

− корни уравнения комплексные сопряженные (k_1,2=α ± jω₀).

1. Корни характеристического уравнения вещественные и разные (k₁≠ k₂).

В этом случае подкоренное выражение в (6.29) положительно, и корни соответственно равны:

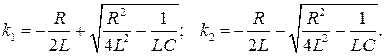
Решением уравнения (6.28) согласно (6.11) и табл.6.1 является выражение

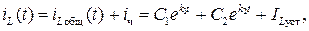(6.30)

где i_ч = I_Lуст − установившееся значение тока в индуктивности после коммутации.

Падение напряжения на индуктивности в переходном режиме

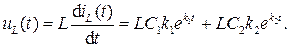(6.31)

Для определения произвольных постоянных С₁ и С₂ необходимо знать независимые и зависимые начальные условия: соответственно ток i_L+0 и напряжение u_L+0 на индуктивности в начальный момент переходного процесса, т.е. при t=t₊₀=0, и установившееся значение тока I_Lуст .

В соответствии с табл. 6.3 i_L+0=0, u_L+0 =E и I_Lуст=0.

Подставляя данные значения в (6.30) и (6.31) и полагая t=t₊₀=0, получим систему уравнений для определения произвольных постоянных:

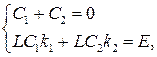
откуда находим: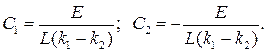

Окончательно ток и напряжение на индуктивности, в переходном режиме имеют вид:

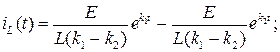(6.32)

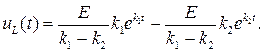(6.33)

Напряжение на емкости легко определяется по выражению (6.32), с учетом соотношения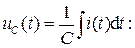

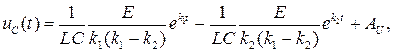(6.34)

где A_U− постоянная интегрирования. Ее значение определяется по величине напряжения на емкости в установившемся режиме: при t=∞ напряжение на емкости равно Е (см. табл.6.3). Тогда, подставив в (6.34) t=∞, получим:

A_U=Е.

Вид кривых напряжения на реактивных элементах и тока в цепи представлены на рис. 6.13.

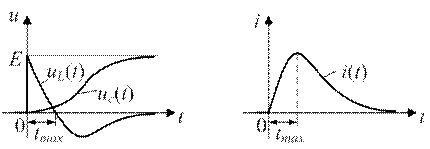
а) б)

Рис. 6.13. Кривые напряжений на реактивных элементах (а)

и тока в цепи (б) в переходном режиме

Напряжение на емкости u_C(t), как и ток i(t) в цепи (ток в индуктивности), в соответствии с законами коммутации в переходном процессе начинают свое изменение от тех значений, которые они имели в момент до коммутации. Напряжение на индуктивности u_L(t) в момент коммутации претерпевает скачок и в процессе переходного режима устремляется к нулю, меняя знак. При этом в момент перехода напряжения на индуктивности через ноль (t=t_max) , ток в цепи достигает максимума.

Сочетание параметров цепи, при котором имеет место апериодический переходный процесс, определяется знаком дискриминанта в (6.29):

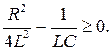
В случае, когда величина емкости и индуктивности фиксированы, критическая величина активного сопротивления, при котором процесс еще апериодический, определяется выражением

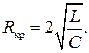(6.35)

2. Корни характеристического уравнения комплексные (k_1,2=α ± jω₀) .

В соответствии с (6.29) приняты обозначения:

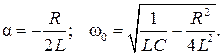(6.36)

Решением уравнения (6.28) согласно (6.11) и табл. 6.1 является выражение

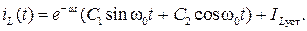(6.37)

Напряжение на индуктивности в переходном режиме (промежуточные преобразования опускаем)

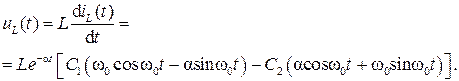(6.38)

Для определения произвольных постоянных С₁ и С₂ необходимо знать независимые и зависимые начальные условия: ток i_L+0 и напряжение u_L+0 на индуктивности в начальный момент переходного процесса, т.е. при t=t₊₀=0, и установившееся значение тока I_Lуст .

В соответствии с табл. 6.3 i_L+0=0, u_L+0 =E и I_Lуст=0.

Подставляя данные значения в (6.37) и (6.38) и полагая t=t₊₀=0, получим систему уравнений для определения произвольных постоянных:

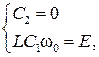
откуда находим: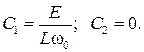

Окончательно выражения для тока и напряжения на индуктивности имеют вид:

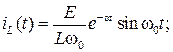(6.39)

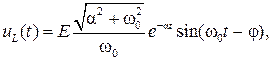
где φ=arctg(ω₀/α).

Полученный результат показывает, что в цепях постоянно тока в переходных режимах при соответствующих соотношениях параметров могут возникать колебательные процессы. Кривая тока в индуктивности приведена на рис. 6.14.

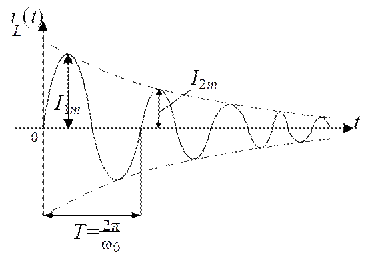
Рис. 6.14. Кривая тока в индуктивности в переходном режиме

Кривая тока представляет собой затухающую синусоиду с периодом T=2π/ω₀. Величина ω₀ носит название частоты свободных колебаний.

Амплитуда тока изменяется по экспоненциальному закону в соответствии с (6.39) . Величина α называется коэффициентом затухания.

Найдем отношение максимумов тока, отстоящих друг от друга на период (I_m1 и I_m2 на рис. 6.14). Очевидно, что гармонические функции принимают одинаковые значения при изменении аргумента на 2π (или изменении t на период), поэтому отношение ∆ соседних амплитуд тока примет вид:

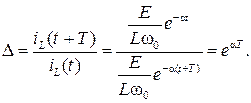
Эта величина носит название декремента колебаний и, как видно из полученного выражения, зависит от коэффициента затухания α и периода колебаний T . Таким образом, декремент колебаний ∆ определяет длительность переходного процесса в цепи второго порядка.

По гармоническому закону с теми же параметрами (α и ω₀) также изменяются и падения напряжения на элементах цепи.

При коммутации, заключающейся в отключении рассмотренной цепи от источника и замыкании ее перемычкой (рис. 6.4), расчет переходного режима ведется аналогично. Студентам предлагается проделать это самостоятельно.