Фильтрация жидкости и газа
Теория фильтрации изучает движение газов, жидкостей и их смесей в порах, т.е. в твердых телах, пронизанных системой сообщающих между собой пустот (пор), что делает их проницаемой для жидкостей. Пористая среда состоит огромного числа случайно расположенных зерен различной формы и величины. Поэтому пространство, в котором движется жидкость, представляет собой систему пор, непрерывно переходящих одна в другую. Для пористой среды характерно свойство сообщаемости пор. Из-за нерегулярности строения порового пространства его нельзя полностью описать никаким конечным набором параметров; для целей теории фильтрации, однако, достаточно небольшого числа осредненных характеристик. Важнейшая характеристика пористой среды – ее пористость 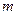 , равная отношению объема, занятого в выделенном элементе порами, к общему объему элемента
, равная отношению объема, занятого в выделенном элементе порами, к общему объему элемента 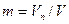 .
.
Самым простым и наиболее изученным случаем нестационарной фильтрации является фильтрация слабосжимаемой жидкости в упругодеформируемом пласте (в технических приложениях эти задачи получили название задач упругого режима фильтрации). В основу исследования кладется система уравнений закона фильтраций и уравнения неразрывности:
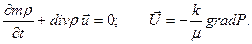
Здесь 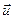 -вектор скорости фильтрации;
-вектор скорости фильтрации; 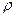 - плотность жидкости. Для того, чтобы получить замкнутую систему уравнений, нужно воспользоваться тем, что свойства жидкости (плотность ρ и вязкость μ), так же как и пористость и проницаемость пористой среды, являются функциями давления (мы предположим движение изотермическим). Исходя, из предположения, слабой сжимаемости жидкости и пористой среды получается уравнение [14-15]:
- плотность жидкости. Для того, чтобы получить замкнутую систему уравнений, нужно воспользоваться тем, что свойства жидкости (плотность ρ и вязкость μ), так же как и пористость и проницаемость пористой среды, являются функциями давления (мы предположим движение изотермическим). Исходя, из предположения, слабой сжимаемости жидкости и пористой среды получается уравнение [14-15]:
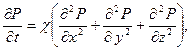 где коэффициент
где коэффициент 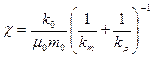 .
.
Здесь 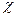 - коэффициент пьезопроводности. Полученное уравнение обычно называется уравнением упругого режима или уравнением пьезопроводности.
- коэффициент пьезопроводности. Полученное уравнение обычно называется уравнением упругого режима или уравнением пьезопроводности.
Рассмотрим постановку основных задач теории упругого режима. Определим распределение давления 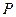 в некоторой замкнутой области пространства D на протяжении промежутка времени 0 ≤ t ≤ T. Из теории уравнения теплопроводности известно, что если задать на границе Г области D линейную комбинацию давления и его производной по нормали к границе области
в некоторой замкнутой области пространства D на протяжении промежутка времени 0 ≤ t ≤ T. Из теории уравнения теплопроводности известно, что если задать на границе Г области D линейную комбинацию давления и его производной по нормали к границе области
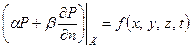
и задать начальное распределение давления в области Д
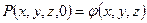 ,
,
то существует распределение давления 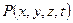 , и притом единственное, удовлетворяющее уравнению пьезопроводности, непрерывное в замкнутой области Д, включая границу, и удовлетворяющие начально-граничным условиям. Сформулированная задача охватывает почти все основные задачи теории упругого режима фильтрации.
, и притом единственное, удовлетворяющее уравнению пьезопроводности, непрерывное в замкнутой области Д, включая границу, и удовлетворяющие начально-граничным условиям. Сформулированная задача охватывает почти все основные задачи теории упругого режима фильтрации.
Рассмотрим подробнее физический смысл тех или иных дополнительных условий. Область, в которой ищется распределения давления жидкости, обычно представляет собой пористый пласт, частично имеющий непроницаемые границы, а частично сообщающийся с другими пластами и вскрывающими его скважинами. На непроницаемых границах должно удовлетворяться очевидное условие отсутствие потока – равенство нормального компонента скорости фильтрации нулю:
Un = 0,
Откуда используя закон Дарси, получаем.
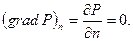
На участках границы с областями, в которых перераспределение давления практически не происходит (область питания), давление можно считать постоянным, так что
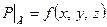 .
.
Такое условие справедливо, если, например, рассматриваемый пласт граничит с высокопроницаемой областью, запас жидкости, в которой весьма велик. Давление на границе такой области близко к среднему давлению в ней и ввиду ее большего объема мало зависит от процессов, происходящих в исследуемой области. Характерным примером является нефтяная залежь, окруженная со всех сторон обширной водоносной областью.
При рассмотрении нестационарных процессов в залежи давление в водоносной области можно считать постоянным. Следует, однако, отчетливо представлять себе, что понятие области постоянного давления не является абсолютным. Чем более длительный характер носят изменения давления, тем на большую область они распространяются.
Часть границы области фильтрации обычно образована стенками скважины и дренажных галерей. На этой части границы чаще всего задается либо давление жидкости, либо поток ее через стенки скважины. Выбор того или иного условия зависит от режима работы скважины или галерей. Могут быть и более сложные условия, когда задается связь давления с расходом жидкости. Задание потока жидкости согласно закону Дарси эквивалентна заданию нормальной производной от давления. Условия этого типа выполняются на тех участках границы, через которые может происходить обмен жидкости с соседними пластами через сравнительно слабопроницаемые перемычки. Если толщина перемычки Δ мала, а давление 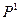 за ней можно считать постоянным, то расход вытекающей жидкости через участок перемычки площадью ds составит
за ней можно считать постоянным, то расход вытекающей жидкости через участок перемычки площадью ds составит 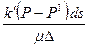 . Это количество жидкости должно быть равно
. Это количество жидкости должно быть равно
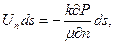
uде Un – нормальная проекция скорости фильтрации на рассматриваемом участке границы. Отсюда имеем
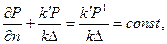
т.е. условия третьего рода.
Все три типа условий являются частными случаями общего условия. Таким образом, задавая начальные распределения давления и указанные условия на границе, получаем однозначно разрешимую задачу.
Задача 3. Одинарное прямолинейно-параллельное движение. Пусть скорость фильтрации жидкости параллельны оси х и не зависит от координат y и z. Давление при этом удовлетворяет уравнению 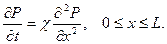 Предположим, что в плоскости х = L давление сохраняет постоянное значение, равное контурному.
Предположим, что в плоскости х = L давление сохраняет постоянное значение, равное контурному.
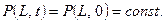
При х = 0 задан расход жидкости q(t). При заданных значениях μ, k, x и L определить давление пласта.
Решение. В работе [5], предполагая, что 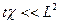 получено решение поставленной задачи. Она описывается в виде:
получено решение поставленной задачи. Она описывается в виде:
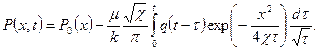
Полученная формула имеет двоякий смысл. С одной стороны, он описывает распределение давления в пласте конечной длины L при малом времени. С другой стороны он дает распределение давления в произвольный момент времени. В пласте «бесконечной» протяженностью L → ∞. Дело в том, что конечное (не бесконечно малое) изменения давления распространяется за заданное время лишь на конечное расстояние и, если рассматриваются малые времена, можно считать пласт бесконечным. Решение задачи для бесконечного пласта автомодельное: независимые переменные х и t входят в решение не порознь, а лишь в комбинации 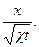
Если 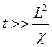 , то [5]
, то [5]
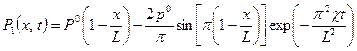
Первый член этого выражения представляет собой стационарное решение, отвечающее заданным краевым условиям
P1(0, t) = P0, P(L, t) = P(L, 0) = const;
второй член выражает основную, при больших временах, часть поправки к этому стационарному решению. Таким образом, приближение к стационарному режиму происходит экспоненционально, причем характерное время выхода на стационарный режим порядка
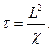
Оценим это время для систем различных режимов. При этом для χ характерное значение х = 104см2/сек. В результате имеем: при L = 1м (переходный процесс в одном пуске-блике породы) t = 0,1сек; при L = 300м (порядка расстояния между скважинами) t = 104сек »3г. L = 1км (порядка размеров месторождения) t = 107сек £ 100 суткам; L = 100км (порядка размеров крупной водонапорной системы) t = 109сек = 30 лет.
В практических расчетах часто приходится рассматривать нестационарные процессы в сложных системах, в которые входят элементы с различными собственными временами. Оценивая время установки (стационарного течения) для каждого элемента по его размерам мы упростим задачу, отделив те элементы, движение в которых уже можно считать стационарными, а те, в которых нестационарный процесс находится в начальной стадии.
Задания для лабораторной работы.
| № п/п | Известные параметры | Определить | Число разбивания |
μ, k, χ, q(t) = α0 t, t £ T, P0 (x)
μ, k, χ, q(t) = α0tsin 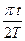 , t £ T, P0 (x)
μ, k, χ, q(t) = α0ttg , t £ T, P0 (x)
μ, k, χ, q(t) = α0ttg 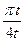 ,t £ T, P0 (x)
μ, k, χ, q(t) = α0t2/(t0 + 2) t £ T, P0 (x)
μ, х, q(t) = α0t, t £ T, P (t1), P1 (t1+ Δt)
k, х, q(t) = α0tsin ,t £ T, P0 (x)
μ, k, χ, q(t) = α0t2/(t0 + 2) t £ T, P0 (x)
μ, х, q(t) = α0t, t £ T, P (t1), P1 (t1+ Δt)
k, х, q(t) = α0tsin  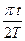 P (t1), P (t1+ Δt)
k, х, q(t) = α0t, ρ (t1), P (t1+ Δt)
μ, х, q(t) = α0tsin P (t1), P (t1+ Δt)
k, х, q(t) = α0t, ρ (t1), P (t1+ Δt)
μ, х, q(t) = α0tsin 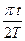 , ρP(t1), P (t1+ Δt)
μ, k, q(t) = α0t, ρ (t1), P(t1+ Δt)
μ, k, q(t) = α0tsin , ρP(t1), P (t1+ Δt)
μ, k, q(t) = α0t, ρ (t1), P(t1+ Δt)
μ, k, q(t) = α0tsin 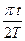 , P(t1), P(t1+ Δt) , P(t1), P(t1+ Δt)
| P (x, t) P (x, t) P (x, t) P (x, t) k, ΔP (x, t) μ, ΔP (x, t) μ, ΔP (x, t) k, ΔP (x, t) x, ΔP (x, t) x, ΔP (x, t) | n=200, 400 n=300, 600 n=400, 800 n=500, 1000 n=250, 500 n=350, 700 n=400, 800 n=500, 1000 n=500, 1000 n=600, 1200 |
Задача 4.Рассмотрим теперь одномерное осесимметричное (плоско-радиальное) движение при упругом режиме. Распределение давления определяется при этом как решение уравнения теплопроводности в полярных координатах (r, j):
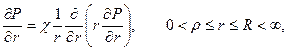
удовлетворяющие начальному условию
P (r, 0) = f(r)
а граничным условиям при r = ρ и r = R.
По прежнему основной интерес представляют решения, отвечающие стационарному начальному распределению давления
f(r)=C1lnr+C2.
В приложениях особое значение имеет задача, в которой на скважине задается не постоянное давление, а постоянный дебит. Решение этой задачи используется в наиболее распространенных способах определения параметров пласта по наблюдениям нестационарного притока к скважине. Положим таким образом
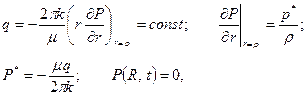
где 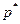 – постоянная размерность давления.
– постоянная размерность давления.
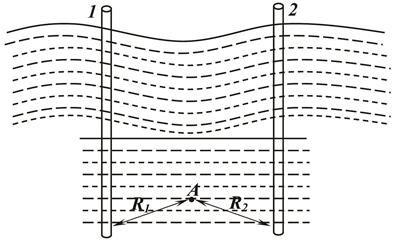
Рис. 7
Предполагая, что 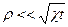 в работе [5] получена решение поставленной задачи в виде
в работе [5] получена решение поставленной задачи в виде
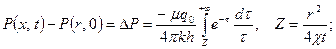 (28)
(28)
Отметим важное обстоятельство: в соотношения для P (r, t) не входит радиус скважины 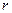 . Это означает, что в области применяемости условия
. Это означает, что в области применяемости условия 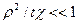 распределения не зависит от радиуса скважины.
распределения не зависит от радиуса скважины.
(28) – является несобственным интегралом, с помощью замены переменной приведем его собственному интегралу. Для этого сделаем замену:
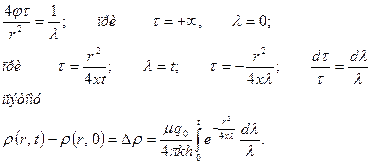
Первоначальное дифференциальное уравнение является линейным, поэтому здесь применим принцип суперпозиции. Если имеется две скважины расположенные друг от друга на расстоянии l, то давление пласта в точке А удаленной от первой скважины на расстоянии будет равен (рис. 7)
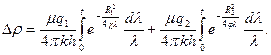
Задания для лабораторной работы
| № п/п | Известные параметры | Определить | Число разбивания |
| k, χ, μн, q1, q2 , R1, R2, t £ T k, χ, μн, q1, q2 , 0 £ х2 + у2 £ R2, t £ T k, χ, μн, q1, q2 , q3, 0 £ х2 + у2 £ R2, t £ T k, χ, μн, q1, q2 , q3, q4, 0 £ х2 + у2 £ R2, t £ T k, χ, μн, q1=q2, 0 £ х2 + у2 £ R2, t £ T k, χ, μн, q1= q2 = q3, 0 £ х2 + у2 £ R2, t £ T | ΔP (t) ΔP(x, у, t) ΔP(x, у, t) ΔP(x, у, t) ΔP(x, у, t) ΔP(x, у, t) | n=500 n=300 n=200 n=300 n=250 n=400 |
Дата добавления: 2015-02-13; просмотров: 1534;
