Формула прямоугольников

Заменим интеграл S_i выражением 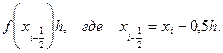Геометрический такая замена означает, что площадь криволинейной трапеции АВСД заменяется площадью прямоугольника АВС₁Д₁ (см. рис. 1).

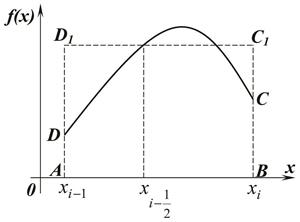
Рис. 1

Тогда получим формулу

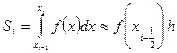(26)

которая называется формулой прямоугольников на частичном отрезке [х_i-1, х_i].

Погрешность метода (26) определяется величиной

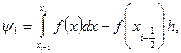
которую легко оценить с помощью формулы Тейлора. Действительно, запишем ψ_i в виде

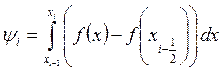
и воспользуемся разложением

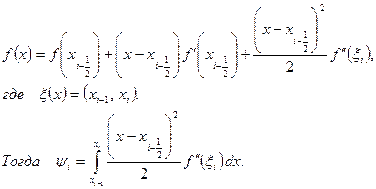
Обозначая 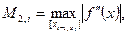оценим ψ_i следующим образом:

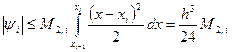
Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива формула

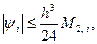
т.е. формула имеет погрешность О(h³) при h→0.

Суммируя равенства (26) по I от 1 до N, получим составную формулу прямоугольников

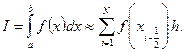
Погрешность этой формулы

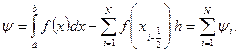
Отсюда, обозначая 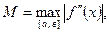получим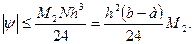

т.е. погрешность формулы прямоугольников на всем отрезке есть величина О(h²). В этом случае говорят, что квадратурная формула имеет второй порядок точности.

Определение. Приближенное равенство

.

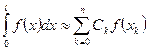Называется квадратурной формулой.