Аналогично, в методе правых прямоугольников
Si = h f(xi), i = 1,2,...,n; 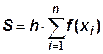 . .
| (6.3) |
И в методе средних прямоугольников
Si = h 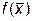 ), i = 0,1,2,...,n-1; ), i = 0,1,2,...,n-1; 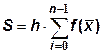 , ,
| (6.4) |
где 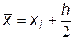 , i = 0,1,2,...,n-1.
, i = 0,1,2,...,n-1.
Приведенные формулы для S являются вычислительными формулами методов прямоугольников.
На рис.6.5. приведена блок-схема вычисления определенного интеграла методом средних прямоугольников.

Рис.6.5. Алгоритм метода средних прямоугольников
Алгоритмы для методов левых и правых прямоугольников отличаются от изображенного на рис.6.5 лишь одним блоком (он выделен жирной линией). Для метода левых прямоугольников здесь должно стоять X=A, для метода правых прямоугольников должно быть X=A+h.
Метод средних прямоугольников имеет меньшую погрешность по сравнению с методом левых или правых прямоугольников и за счет коэффициента в знаменателе (24 > 2), и за счет интеграла от производной, т.к. для большинства функций выполняется неравенство 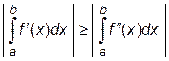 .
.
Следовательно, использование метода средних прямоугольников является предпочтительным, но использовать его удается не всегда. Если значения f(x) определяются из эксперимента в дискретном наборе узлов, то метод средних прямоугольников напрямую применить нельзя из-за отсутствия значений f(x) в срединных точках. В этой ситуации приходится применять либо какие-нибудь средства интерполяции, что приводит к дополнительным расходам машинного времени и памяти, либо другие методы численного интегрирования.
Дата добавления: 2015-01-15; просмотров: 3748;
