О векторном методе анализа цепей переменного тока.

При включении переменной э.д.с. в последовательную электрическую R, L и C – цепь в ней происходят вынужденные колебания зарядов. Колебания э.д.с. на входе цепи и напряжений на элементах R, L и C могут совпадать или не совпадать по фазе с колебаниями квазистационарного тока. Для получения формулы полного сопротивления цепи переменному току и расчета сдвига по фазе между током и напряжением можно воспользоваться векторной диаграммой, в которой:

1) мгновенное значение разности потенциалов на концах участка цепи, падений напряжений на элементах R, L и C ( 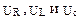) и силы тока (i) численно равны проекциям на произвольно выбранную ось векторов амплитудных значений этих величин ( 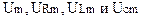), вращающихся, портив часовой стрелки, вокруг общей оси с частотой вынуждающей э.д.с.;

2) условные векторы ( 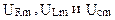) изображаются на одном рисунке с вектором 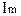так, чтобы было выполнено фазовое соотношение между ними;

3) векторная сумма 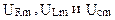равна .

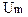Всякий проводник обладает не только активным сопротивлением, но и некоторой емкостью и индуктивностью. Поэтому понятие о “чистом” активном сопротивлении, “чистой” индуктивности L или емкости C является абстрактным.

Ниже будут построены векторные диаграммы и рассмотрены фазовые соотношения между током и напряжением для идеализированных цепей и реальной последовательной R, L и C – цепи.